Toán lớp 12: Mặt cầu ngoại tiếp hình chóp mới nhất 2023

Bạn đang xem bài viết Mặt cầu ngoại tiếp hình chóp. Hi vọng sẽ là đáp án bạn ưng ý. Cùng theo dõi nhé!

Ở bài viết này, Cấp Nước Lào Cai sẽ giúp độc giả tổng hợp các công thức giải nhanh phần mặt cầu ngoại tiếp hình chóp trong chương trình toán 12 và một số bài tập vận dụng có lời giải.

Tóm tắt

Lý thuyết về mặt cầu ngoại tiếp hình chóp

Điều kiện cần và đủ để hình chóp S.A₁A₂…A_n có mặt cầu ngoại tiếp là đa giác đáy A₁A₂…A_n phải là đa giác nội tiếp.

Chứng minh:

+) Điều kiện cần:

Giả sử tồn tại mặt cầu tâm O ngoại tiếp hình chóp S.A₁A₂…A_n, tức là ta có OS = OA₁ = OA₂ = … = OA_n (1)

Kẻ OH vuông góc mặt phẳng đáy (A₁A₂…A_n)

HA₁ = HA₂ = … = HA_n (2)

Đẳng thức (2) chứng tỏ đáy A₁A₂…A_n là một đa giác nội tiếp.

+) Điều kiện đủ

Giả sử A₁A₂…A_n là một đa giác nội tiếp. Gọi H là tâm đường tròn ngoại tiếp đáy. Qua H dựng đường thẳng ∆ vuông góc (A₁A₂…A_n). Vẽ mặt phẳng trung trực (P) của một cạnh bất kì của hình chóp (chẳng hạn cạnh SA₁).

Do ∆ không song song (P) nên giả sử ∆ ∩ (P) = O

Khi đó ta thấy OA₁ = OA₂= … = OA_n, OA₁= OS.

Từ đó suy ra O là tâm mặt cầu ngoại tiếp hình chóp đa giác A₁A₂…A_n.

Chú ý: Từ định lí trên ta rút ra các kết luận sau:

Nói riêng mọi hình chóp tam giác (tứ diện), mọi hình chóp đều, đều có mặt cầu ngoại tiếp

Các phương pháp xác định tâm mặt cầu ngoại tiếp hình chóp.

Bài toán: Xác định tâm I và tính bán kính R của mặt cầu ngoại tiếp hình chóp A₁A₂…A_n.

Phương pháp 1: Gọi I là tâm mặt cầu ngoại tiếp hình chóp S.A₁A₂…A_n.

+) Xác định tâm O đường tròn ngoại tiếp đa giác đáy A₁A₂…A_n

+) Dựng trục ∆ của đường tròn ngoại tiếp đa giác đáy A₁A₂…A_n (∆ là đường thẳng đi qua tâm O đường tròn ngoại tiếp đa giác đáy và vuông góc với mặt phẳng đáy)

+) Vẽ mặt phẳng trung trực (P) của một cạnh bên bất kì của hình chóp.

+) Giả sử I = ∆ ∩ (P) khi đó I là tâm mặt cầu ngoại tiếp cần dựng.

Lưu ý:

Trong trường hợp sau đây mặt phẳng trung trực có thể thay bằng đường trung trực.

+) Khi hình chóp đều (vì ∆ đi qua đỉnh S)

+) Khi hình chóp có một cạnh vuông góc với mặt phẳng đáy

Có thể phát hiện trục ∆ dựa vào tính chất của một số hình chóp đặc biệt rồi chứng minh thay vì dựng ∆.

Khi dựng mặt phẳng trung trực của cạnh bên nên chọn cạnh bên của hình chóp đồng phẳng với trục ∆ để dễ dàng tính toán bán kính R.

Phương pháp 2: Gọi I là tâm mặt cầu ngoại tiếp hình chóp A₁A₂…A_n

+) Dựng trục ∆₁ của đường tròn ngoại tiếp đa giác đáy A₁A₂…A_n (∆ là đường thẳng đi qua tâm O đường tròn ngoại tiếp đa giác đáy và vuông góc với mặt phẳng đáy.)

+) Dựng trục ∆₂ của đường tròn ngoại tiếp tam giác của mặt bên sao cho ∆₁ ∆₂ đồng phẳng

+) Giả sử I = ∆₁ ∩ ∆₂ khi đó I là tâm mặt cầu ngoại tiếp.

Phương pháp 3:

Ta chứng minh các đỉnh của hình chóp cùng nhìn hai đỉnh còn lại của hình chóp dưới một góc vuông hoặc tất cả các đỉnh của hình chóp cùng nhìn hai điểm nào đó dưới một góc vuông.

Phương pháp 4: Trong không gian ta dự đoán điểm đặc biệt I nào đó rồi chứng minh I cách đều các đỉnh của hình chóp.

Cách xác định tâm và tính bán kính mặt cầu ngoại tiếp của một số hình chóp đặc biệt.

Trường hợp hình chóp có các cạnh bên bằng nhau.

+) Giả sử SA = SB = SC = SD. Ta dựng SO ⊥ (ABCD). Trong tam giác SAO kẻ trung trực của SA cắt SO tại I. Ta được I là tâm của mặt cầu ngoại tiếp.

+) Trường hợp này để tính bán kính ta sử dụng tứ giác nội tiếp đường tròn. Cụ thể ABCD nội tiếp đường tròn và có AB cắt CD tại M, khi đó MA.MB = MC.MD.

Trường hợp hình chóp có một mặt vuông góc với đáy.

+) Xác định trục đường tròn ngoại tiếp đáy

+) Xác định trục đường tròn ngoại tiếp của mặt vuông góc đáy

+) Giao của hai trục đường tròn là tâm đường tròn ngoại

Trường hợp hình chóp có một cạnh vuông góc với đáy.

Giả sử SA vuông góc (ABCD).

+) Xác định trục d đường tròn ngoại tiếp đáy, d song song SA.

+) Xác định trung trực cạnh bên SA cắt d tại I thì I là tâm mặt cầu ngoại tiếp.

Để tính bán kính ta sử dụng định lý Pitago trong tam giác vuông

Bài tập vận dụng mặt cầu ngoại tiếp hình chóp

Ví dụ 1: Cho hình chóp S.ABCD có chiều cao SA = a, đáy ABCD là hình thang vuông tại A và B với AB = BC = a, AD = 2a. Gọi E là trung điểm AD. Xác định tâm và tính bán kính mặt cầu ngoại tiếp SCDE theo a.

Phân tích bài toán:

+) Nếu nhìn S.CDE là hình chóp tam giác S.CDE có mặt đáy CDE là tam giác vuông tại E, ta có ngay trục d đường tròn ngoại tiếp tam giác CDE, khi đó ta tìm trục d’ đường tròn ngoại tiếp tam giác chứa mặt bên nào đó của hình chóp sao cho d và d’ đồng phẳng hoặc tìm hay dựng mặt phẳng trung trực của một cạnh bên nào đó của hình chóp, trong trường hợp này không nên dựng mặt phẳng trung trực của một cạnh bên bất kì, vì các cạnh bên của hình chóp không đồng phẳng với d.

+) Nếu nhìn S.DCE là hình chóp C.SDE đáy tam giác SCE thì trục đường tròn ngoại tiếp tam giác SCD sẽ song song CE, khi đó ta có thể dựng mặt phẳng trung trực của CE cắt trục tại tâm I.

Từ đó ví dụ 1 có thể có các cách giải sau

Cách giải thứ nhất.

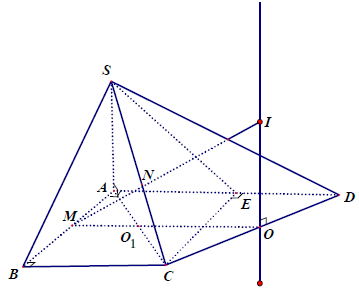
Tam giác CDE vuông tại E nên gọi O là trung điểm CD và d là đường thẳng qua O song song

SA khi đó d là trục đường tròn ngoại tiếp đáy CDE.

Gọi M, N lần lượt là trung điểm AB và SC.

Ta chứng minh được MN là trục đường tròn M ngoại tiếp tam giác SEC

Thật vậy

CE ⊥ SE nên N là tâm đường tròn ngoại tiếp tam giác SCE.

Dễ dàng chứng minh được MN và d cắt nhau

Gọi I = MN ∩ d, khi đó I là tâm mặt cầu ngoại tiếp S.CDE

Bán kính , trong đó

, suy ra

Cách giải thứ hai.

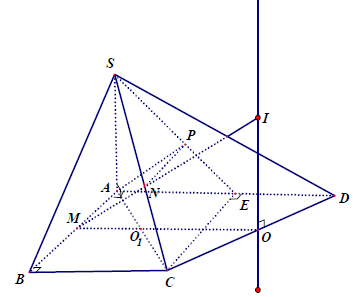
Gọi M, N, P lần lượt là trung điểm của AB, SC và SE

Ta có AMNP là hình bình hành và (AMNP) là mặt phẳng trung trực SE, vì:

AP ⊥ SE (Tam giác ASE cân tại A)

NP ⊥ SE NP // AB, AB ⊥ SE).

Gọi O là trung điểm CD ta có O là tâm đường tròn ngoại tiếp tam giác CDE.

Đường thẳng d đi qua O song song SA là trục đường tròn ngoại tiếp đáy ECD.

MN ⊂ (AMNP) cắt d tại I, ta được I là tâm mặt cầu ngoại tiếp S.ECD.

Bán kính

Trong đó , suy ra

Cách giải thứ ba:

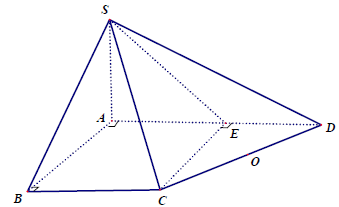
Nếu nhìn tứ diện S.ECD là hình chóp C.SED ta có đường cao CE và mặt đáy là tam giác SED, có góc SED > 90°.

Gọi O là tâm đường tròn ngoại tiếp tam giác SDE và d là trục đường tròn ngoại tiếp đáy SDE. Khi đó d // CE.

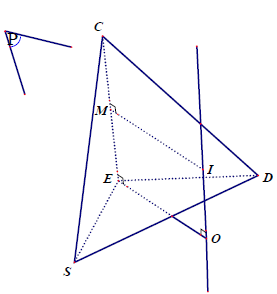
Dựng mặt phẳng trung trực (P) của CE đi qua trung điểm M của CE cắt d tại I.

Ta được I là tâm mặt cầu ngoại tiếp CSDE.

Bán kính

Với R₁ = OE là bán kính đường tròn ngoại tiếp tam giác SED.

Tam giác SED có

Theo định lí hàm số côsin ta tính được góc SED = 135°

Theo định lí hàm . Suy ra .

Ví dụ 2: Cho hình S.ABCD, đường cao SA = 2a đáy ABCD là hình thang cân đáy lớn AD = 2a, AB = BC = CD = a. Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABC.

Phân tích bài toán.

+) Hình chóp S.ABC có SA là đường cao nên theo phương pháp giải chúng ta có thể sử dụng đúng phương pháp dựng tâm mặt cầu ngoại tiếp chóp S.ABC. Có trục đường tròn ngoại tiếp đáy song song SA như vậy sẽ chọn mặt phẳng trung trực của cạnh SA, xác định thêm tâm đường tròn ngoại tiếp tam giác ABC là xong.

+) Đáy là hình thang cân với AD = 2a, AB = BC = CD = a nên ta nghĩ đến việc xem xét các quan hệ vuông góc từ số liệu bài toán và định lí 3 đường vuông góc để chứng minh A, B, C cùng nhìn SD dưới một góc vuông.

Từ đó ta có các cách giải sau:

Cách giải thứ nhất

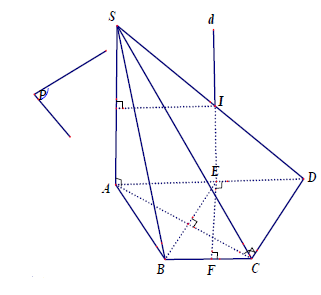
Gọi E, F lần lượt là trung điểm AD và BC có BE là trung trực AC và EF là trung trực BC nên E là tâm đường tròn ngoại tiếp tam giác ABC.

Trong mp (SAD) đường thẳng d qua E song song SA là trục đường tròn ngoại tiếp tam giác ABC.

Gọi (P) là mặt phẳng trung trực SA.

khi đó (P) ∩ d = I là tâm mặt cầu ngoại tiếp chóp S.ABC

Bán kính

Cách giải thứ hai.

Ta có SA ⊥ AD.

Gọi E là trung điểm AD khi đó EC = ED = EA = a

Nên AC ⊥ CD suy ra SC ⊥ CD

Tương tự SB ⊥ BD

Do đó A, B, C, S, D nằm trên mặt cầu đường kính SD.

Bán kính mặt cầu ngoại tiếp S.ABC là

Ví dụ 3: Cho hình chóp S.ABC có SA vuông góc mặt phẳng (ABC). AC = b, AB = c, góc BAC = α. Gọi B’, C’ lần lượt là hình chiếu vuông góc của A lên SB, SC. Xác định tâm và tính bán kính mặt cầu đó theo b, c và α.

Cách giải thứ nhất.

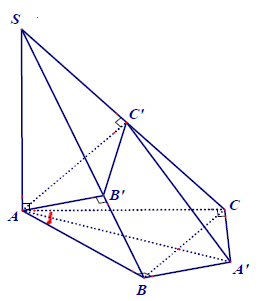
Gọi AA’ là đường kính của đường tròn ngoại tiếp tam giác ABC.

Khi đó AC ⊥ A’C, AB ⊥ A’B.

Ta chứng minh AC’ ⊥ A’C’:

SA ⊥ A’C (do SA ⊥ (ABC))

AC ⊥ A’C

⇒ A’C ⊥ AC’.

Mà AC’ ⊥ SC ⇒ AC’ ⊥ A’C’

Tương tự AB’ ⊥ A’B’

Như vậy B, C, B’, C’ cùng nhìn AA’ dưới một góc vuông nên A, B, C, C’, B’ cùng thuộc mặt cầu đường kính AA’.

Tính bán kính: Gọi R là bán kính mặt cầu đi qua A, B, C, C’, B’ thì R cũng là bán kính đường tròn ngoại tiếp tam giác ABC.

Trong tam giác ABC: BC² = AB² + AC² − 2AB.AC.cosA = c² + b² − 2bc.cos α

⇒

Trong tam giác ABC:

Vậy tâm mặt cầu ngoại tiếp A.BCC’B’ là I trung điểm AA’ bán kính

Cách giải thứ 2:

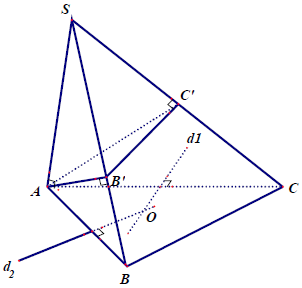
Tam giác ABB’ vuông tại B’ nên trong (ABC) dựng đường trung trực d₂của AB, tam giác ACC’ vuông tại C’ nên trong mp (ABC) dựng đường trung trực d₁ của AC.

Gọi O = d₁ ∩ d₂, ta có OA = OB = OB’ = OC = OC’ nên O là tâm mặt cầu ngoại tiếp ABCC’B’ đồng thời là tâm đường tròn ngoại tiếp tam giác ABC

Bán kính R = OA

Trong tam giác ABC:

Phương pháp tính nhanh bán kính mặt cầu ngoại tiếp các loại

Loại 1: Hình chóp có các đỉnh nhìn đoạn thẳng nối 2 đỉnh còn lại dưới 1 góc vuông.

Gọi d là độ dài đoạn thẳng trên thì ta có bán kính mặt cầu ngoại tiếp là:

Ví dụ: Cho hình chóp SABC có tam giác ABC vuông tại B, SA vuông góc với mặt phẳng (ABC) và SC = 2a. Tính diện tích và thể tích mặt cầu ngoại tiếp hình chóp trên

Giải

Dễ thấy tam giác SAC vuông tại A, tam giác SBC vuông tại B từ đó hình chóp này loại 1 nên

Ví dụ: Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA vuông góc với mặt phẳng (ABCD) và SC = 2a. Tính diện tích và thể tích mặt cầu ngoại tiếp hình chóp trên

Giải

Dễ thấy tam giác SAC vuông tại A, tam giác SBC vuông tại B và giác SDC vuông tại D từ đó hình chóp này loại 1 nên:

Loại 2: Hình chóp đều

Gọi h là độ cao hình chóp và k là chiều dài cạnh bên thì ta có bán kính mặt cầu là:

Ví dụ: Cho hình chóp tam giác đều S.ABC, có AB = a và cạnh bên SA = 2a, tính diện tích và thể tích mặt cầu ngoại tiếp hình chóp trên

Giải

Gọi G là trọng tâm tam giác thì ta có SG vuông góc với mặt phẳng (ABC)

Thế thì SA = k, SG = h nên R mặt cầu:

Ví dụ: Cho hình chóp tứ giác đều S.ABCD, có AB = a và cạnh bên SA = 2a, tính diện tích và thể tích mặt cầu ngoại tiếp hình chóp trên

Giải

Gọi O là tâm hình vuông ABCD thì ta có SO vuông góc với mặt phẳng (ABCD)

Thế thì SA = k, SO = h nên R mặt cầu:

Loại 3: Hình chóp có cạnh bên vuông góc với đáy

Gọi H là chiều cao hình chóp và R_d là bán kính của đáy thì bán kính mặt cầu:

Ví dụ: cho hình chóp SABCD có cạnh SA vuông góc với đáy, ABCD là hình chữ nhật có đường chéo dài , SA = 2a. Tính diện tích và thể tích mặt cầu ngoại tiếp S.ABCD

Giải

Ta có và SA = h. Áp dụng công thức ta có:

Ví dụ: Cho hình chóp S.ABC có cạnh SA vuông góc với đáy, ABC là tam giác đều cạnh a, SA dài 2a. Tính diện tích và thể tích mặt cầu ngoại tiếp S.ABCD

Giải

Ta có và SA = h

Áp dụng công thức ta có:

Ví dụ: Cho hình chóp S.ABC có cạnh SA vuông góc với đáy, ABC là tam giác vuông tại A và BC = 2a, SA dài 2a. Tính diện tích và thể tích mặt cầu ngoại tiếp S.ABCD

Giải

Ta có và SA = h.

Áp dụng công thức ta có:

Ví dụ: cho hình chóp S.ABC có cạnh SA vuông góc với đáy, ABC là tam giác cân tại A và AB = a và góc A = 120°, SA dài 2a. Tính diện tích và thể tích mặt cầu ngoại tiếp S.ABC

Giải

Ta có và SA = 2a

Áp dụng công thức ta có:

Diện tích

Thể tích

Loại 4: Hình chóp có mặt bên vuông góc với đáy

Đối với loại này thì mặt bên vuông góc thường là tam giác vuông, tam giác cân hoặc đều

Gọi h là chiều cao hình chóp và R_b, R_d là bán kính của mặt bên, mặt đáy, GT là độ dài giao tuyến của mặt bên và đáy thì bán kính mặt cầu:

Ví dụ: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích mặt cầu ngoại tiếp khối chóp

Giải:

Giao tuyến của mặt bên và đáy là: GT = AB, bán kính đáy , bán kính mặt bên (SAB) là