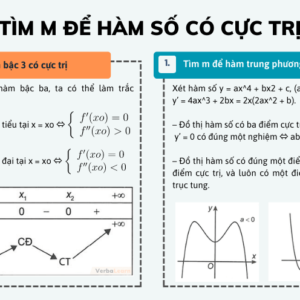
Bạn đang xem bài viết Phân dạng và cách giải. Hi vọng sẽ là đáp án bạn ưng ý. Cùng theo dõi nhé!
Bài toán tìm giá trị lớn nhất (GTLN), giá trị nhỏ nhất (GTNN) của hàm số xuất hiện khá thường xuyên trong các đề thi toán học. Với nhiều mức độ, nhiều dạng khác nhau. Hiểu được sự khó khăn của học sinh khi bắt đầu tiếp xúc với các dạng bài này, bài học hôm nay Cấp Nước Lào Cai sẽ tổng hợp lại chi tiết các dạng toán và kiến thức liên quan đến GTLN, GTNN trong toán học và đặc biệt là chương trình toán lớp 12.
Lý thuyết
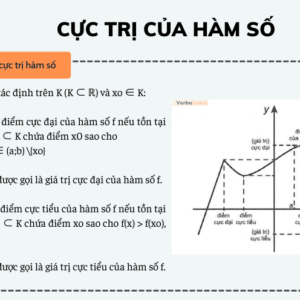
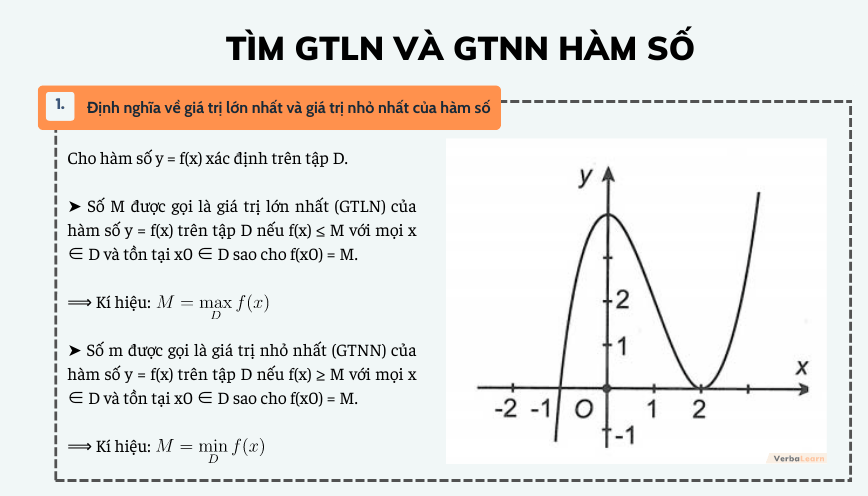
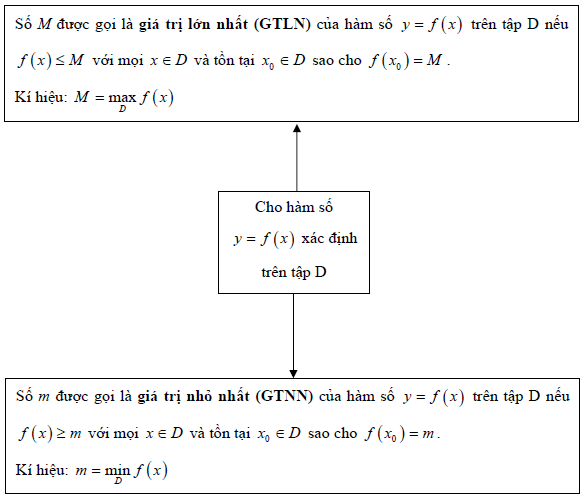
Cho hàm số y = f(x) xác định trên tập D.
+) Số M được gọi là giá trị lớn nhất (GTLN) của hàm số y = f(x) trên tập D nếu f(x) ≤ M với mọi x ∈ D và tồn tại x0 ∈ D sao cho f(x0) = M.
Kí hiệu:
+) Số m được gọi là giá trị nhỏ nhất (GTNN) của hàm số y = f(x) trên tập D nếu f(x) ≥ M với mọi x ∈ D và tồn tại x0 ∈ D sao cho f(x0) = M.
Kí hiệu:
⟹ Sơ đồ hệ thống hóa giá trị nhỏ nhất, giá trị lớn nhất của hàm số
Phân dạng bài tập
Thông thường đối với các bài giảng về giá trị lớn nhất giá trị nhỏ nhất chỉ có cơ bản vài dạng bài tập. Tuy nhiên đối với một bài viết tổng quan về chuyên đề như này thì Cấp Nước Lào Cai chia thành 13 dạng từ cơ bản, vận dụng cho đến vận dụng cao. Nếu các dạng bài tập quá dài bạn đọc có thể tải các tài liệu về để xem một cách dễ dàng hơn.
Dạng 1: Tìm giá trị lớn nhất nhỏ nhất của hàm số y = f(x) trên một khoảng
Phương pháp giải
Ta thực hiện các bước sau:
- Bước 1. Tìm tập xác định (nếu đề chưa cho khoảng)
- Bước 2. Tính y’ = f’(x); tìm các điểm mà đạo hàm bằng không hoặc không xác định.
- Bước 3. Lập bảng biến thiên
- Bước 4. Kết luận
Lưu ý: Có thể dùng máy tính cầm tay để giải theo các bước như sau:
Bước 1. Để tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = f(x) trên miền (a;b) ta sử dụng máy tính Casio với lệnh MODE 7 (MODE 9 lập bảng giá trị)
Bước 2. Quan sát bảng giá trị máy tính hiển thị, giá trị lớn nhất xuất hiện là max, giá trị nhỏ nhất xuất hiện là min.
– Ta thiết lập miền giá trị của biến x Start a End b Step (có thể làm tròn để Step đẹp).
Chú ý: Khi đề bài liên có các yếu tố lượng giác sinx, cosx, tanx… ta chuyển máy tính về chế độ Radian.
Bài tập vận dụng
Câu 1. Cho hàm số . Khẳng định nào sau đây đúng?
A.
B.
C.
D. Hàm số không tồn tại giá trị lớn nhất
Hướng dẫn giải
Chọn B
Tập xác định D = ℝ
Ta có f’(x) = -2x5 + 2x4 – x + 1 = – (x – 1)(2x4 + 1)
Khi đó f’(x) = 0 ⇔ – (x – 1)(2x4 + 1) = 0 ⇔ x = 1
Bảng biến thiên
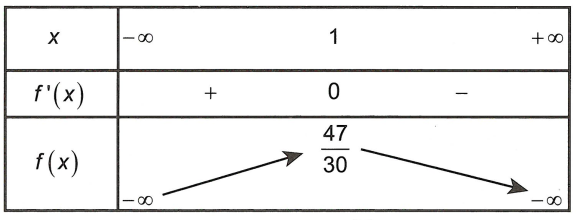
Dựa vào bảng biến thiên, ta thấy tại x = 1
Câu 2. Gọi a là giá trị lớn nhất của hàm số trên khoảng (-∞; 1). Khi đó giá trị của biểu thức
bằng
A.
B.
C.
D.
Hướng dẫn giải
Chọn C
Hàm số liên tục trên khoảng (-∞; 1)
Ta có
Khi đó f’(x) = 0 ⇔ 8x2 – 12x – 8 = 0 ⇔
Bảng biến thiên
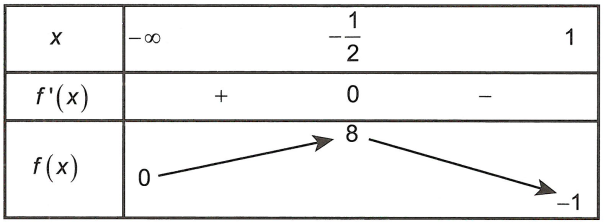
Dựa vào bảng biến thiên, ta thấy
Câu 3. Cho hàm số . Trong các khẳng định sau, khẳng định nào đúng?
A.
B.
C.
D. Hàm số không có giá trị nhỏ nhất
Hướng dẫn giải
Chọn B
Tập xác định D = ℝ
Ta có
Do đó y’ = 0 ⇔ 2x2 – 2 = 0 ⇔ x = ±1
Bảng biến thiên
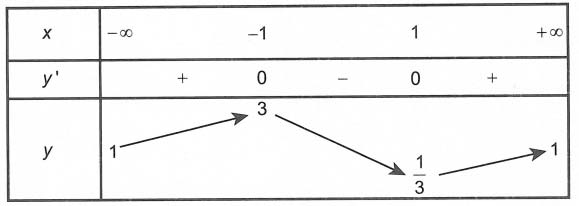
Dựa vào bảng biến thiên, ta thấy tại x = 1
Dạng 2: Tìm giá trị lớn nhất nhỏ nhất của hàm số trên một đoạn
Phương pháp giải
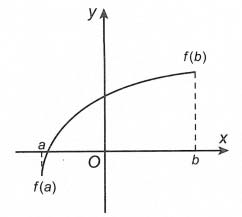
- Bước 1. Tính f’(x)
- Bước 2. Tìm các điểm xi ∈ (a;b) mà tại đó f’(xi) = 0 hoặc f’(xi) không xác định
- Bước 3. Tính f(a), f(xi), f(b)
- Bước 4. Tìm số lớn nhất M và số nhỏ nhất m trong các số trên.
Khi đó và
Chú ý:
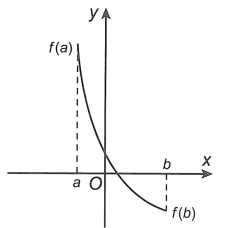
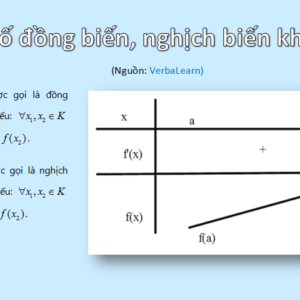
– Hàm số y = f(x) đồng biến trên đoạn [a;b] thì
– Hàm số y = f(x) nghịch biến trên đoạn [a;b] thì
Bài tập vận dụng
Câu 1. Cho hàm số . Giá trị của
bằng
A. 16
B.
C.
D.
Hướng dẫn giải
Chọn D
Ta có ; do đó hàm số nghịch biến trên mỗi khoảng (-∞; 1); (1; +∞)
⇒ Hàm số nghịch biến trên [2; 3].
Do đó
Vậy
Câu 2. Gọi M, m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số . Giá trị của biểu thức P = M + m bằng
A.
B.
C.
D.
Hướng dẫn giải
Chọn A
Tập xác định D = [-2; 2]
Ta có , x ∈ (-2; 2)
y’ = 0 ⇔
Vậy
Câu 3. Giá trị nhỏ nhất của hàm số y = 2x3 – 3x2 + m trên đoạn [0; 5] bằng 5 khi m bằng
A. 6
B. 10
C. 7
D. 5
Hướng dẫn giải
Chọn A.
Hàm số xác định và liên tục trên D = [0; 5]
Ta có y’ = 0 ⇔ 6x2 – 6x = 0 ⇔
f (0) = m; f (1) = m – 1; f (5) = 175 + m
Dễ thấy f (5) > f (0) > f (1), ∀ m ∈ ℝ nên
Theo đề bài ⇔ m – 1 = 5 ⇔ m = 6
Câu 4. Gọi A, B là giá trị nhỏ nhất, giá trị lớn nhất của hàm số trên đoạn [2; 3]. Tất cả các giá trị thực của tham số m để
là
A. m = 1; m = -2
B. m = -2
C. m = ±2
D. m = -1; m = 2
Hướng dẫn giải
Chọn A
Hàm số đã cho liên tục trên đoạn [2; 3]
Ta có
Do đó
⇔ 3m2 + m – 6 = 0 ⇔
Câu 5. Biết hàm số y = x3 + 3mx2 + 3(2m – 1) x + 1 (với m là tham số) trên đoạn [-2; 0] đạt giá trị lớn nhất bằng 6. Các giá trị của tham số m là
A. m = 1
B. m = 0
C. m = 3
D. m = -1
Hướng dẫn giải
Chọn D
y’ = 0 ⇔
Vì y(-2) = -1; y(0) = 1 và theo bài ra nên giá trị lớn nhất không đạt tại x = -2; x = 0.
Do đó giá trị lớn nhất đạt tại y(-1) hoặc y(1 – 2m).
Ta có y(-1) = -3m + 3; y(1 – 2m) = (1 – 2m)2(m – 2) + 1
Trường hợp 1: Xét -3m + 3 = 6 ⇔ m = -1
Thử lại với m = -1, ta có y’ = 0 ⇔ nên m = -1 là một giá trị cần tìm.
Trường hợp 2: Xét
Vì ⇒ m – 2 < 0 ⇒ (1 – 2m)2(m – 2) < 0 nên (1) vô nghiệm
Dạng 3: Tìm giá trị lớn nhất nhỏ nhất của hàm số y = |f(x)| trên đoạn [a; b]
Phương pháp giải
Thực hiện theo các bước sau
– Bước 1. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số f(x) trên đoạn [a; b], giả sử thứ tự là M, m.
– Bước 2.
+) Tìm
+) Tìm
Trường hợp 1: M․m < 0 ⇒ = 0
Trường hợp 1: m ≥ 0 ⇒ = m
Trường hợp 1: M ≤ 0 ⇒ = |M| = -M
– Bước 3. Kết luận.
* Tìm tham số để GTLN của hàm số y = |f(x)| trên đoạn [α, β] bằng k. Thực hiện theo các bước sau:
– Bước 1. Tìm
– Bước 2. Xét các trường hợp
+) |A| = k tìm m, thử lại các giá trị m đó
+) |B| = k tìm m, thử lại các giá trị m đó
Bài tập vận dụng
Câu 1. Giá trị nhỏ nhất của hàm số y = |x3 – 9x2 + 24x – 68| trên đoạn [-1; 4] bằng
A. 48
B. 52
C. -102
D. 0
Hướng dẫn giải
Chọn A
Bảng biến thiên của hàm số y = x3 – 9x2 + 24x – 68 trên đoạn [-1; 4]
![Dạng 3: Tìm giá trị lớn nhất nhỏ nhất của hàm số y = |f(x)| trên đoạn [a; b]](https://verbalearn.org/wp-content/uploads/2020/05/tim-gia-tri-lon-nhat-nho-nhat-cua-ham-so-7.png)
Suy ra bảng biến thiên của hàm số y = |x3 – 9x2 + 24x – 68| trên đoạn [-1; 4] là
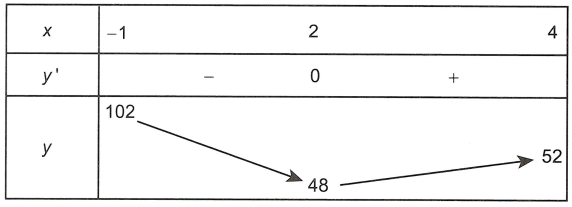
Vậy giá trị nhỏ nhất của hàm số y = |x3 – 9x2 + 24x – 68| trên đoạn [-1; 4] bằng 48.
Cách khác: Theo trường hợp 3 thì M = -48 < 0 ⇒ min y = 48
Câu 2. Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số trên đoạn [1; 2] bằng 2.
Số phần tử của tập S là
A. 3
B. 1
C. 4
D. 2
Hướng dẫn giải
Chọn D
Xét hàm số
Ta có
Mặt khác
Do đó
– Trường hợp 1:
+) Với (loại)
+) Với (thỏa mãn)
– Trường hợp 2:
+) Với (thỏa mãn)
+) Với (loại)
Vậy có hai giá trị của m thỏa mãn.
Câu 3. Gọi S là tập các giá trị nguyên của tham số m sao cho giá trị lớn nhất của hàm số f(x) = |¼ x4 – 14x2 + 48x + m – 30| trên đoạn [0; 2] không vượt quá 30. Tổng các phần tử của S bằng
A. 108
B. 120
C. 210
D. 136
Hướng dẫn giải
Chọn D
Xét hàm số g(x) = ¼ x4 – 14x2 + 48x + m – 30 trên đoạn [0; 2]
Ta có g’(x) = x3 – 28x + 48 ⇒ g’(x) = 0 ⇔
Để
⇒ m ∈ {0; 1; 2; …; 15; 16}
Tổng các phần tử của S là 136.
Câu 4. Biết giá trị lớn nhất của hàm số bằng 18.
Mệnh đề nào sau đây đúng?
A. 0 < m < 5
B. 10 < m < 15
C. 5 < m < 10
D. 15 < m < 20
Hướng dẫn giải
Chọn D
Xét hàm số liên tục trên tập xác định [-2; 2]
Ta có
Do đó khi x = -2, suy ra giá trị lớn nhất của hàm số bằng
Theo bài ra = 18 ⇔ m = 15,5. Vậy 15 < m < 20
Dạng 4: Tìm điều kiện tham số để GTLN của hàm số y = |f(x) + g(m)| trên đoạn [a; b] đạt GTNN
Phương pháp giải
Thực hiện các bước sau
– Bước 1. Tìm
– Bước 2. Gọi M là giá trị lớn nhất của số y = |f(x) + g(m)| thì
M = max{|α + g(m)|; |β + g(m)|}≥
Dấu bằng xảy ra khi và chỉ khi |α + g(m)| = |β + g(m)|
Áp dụng bất đẳng thức
Dấu bằng xảy ra khi và chỉ khi [α + g(m)]․[β + g(m)] ≥ 0
– Bước 3. Kết luận khi
Bài tập vận dụng
Câu 1. Biết rằng giá trị lớn nhất của hàm số y = |x2 + 2x + m – 4| trên đoạn [-2; 1] đạt giá trị nhỏ nhất, giá trị của tham số m bằng
A. 1
B. 3
C. 4
D. 5
Hướng dẫn giải
Chọn B
Đặt f(x) = x2 + 2x
Ta có f’(x) = 2x + 2
f’(x) = 0 ⇔ x = -1 ∈ [-2; 1]
f (-2) = 0; f (1) = 3; f (-1) = -1
Do đó
Suy ra
Dấu bằng xảy ra khi và chỉ khi
⇒ m = 3 (thỏa mãn)
Câu 2. Để giá trị lớn nhất của hàm số đạt giá trị nhỏ nhất thì m bằng
A.
B.
C.
D.
Hướng dẫn giải
Chọn A
Tập xác định D = [0; 2]
Đặt , x ∈ D
Ta có ⇒ f’(x) = 0 ⇔ x = 1
f (0) = 0; f (2) = 0; f (1) = 1
Suy ra
Dấu bằng xảy ra ⇔ (thỏa mãn)
Suy ra giá trị lớn nhất của hàm số là nhỏ nhất khi
Câu 3. Giá trị nhỏ nhất của hàm số y = f (x, m) = |x2 – 2x + 5| + mx đạt giá trị lớn nhất bằng
A. 2
B. 5
C. 8
D. 9
Hướng dẫn giải
Chọn B
Ta có min f (x, m) ≤ f (0, m) = 5, ∀ m ∈ ℝ
Xét m = 2 ta có f (x, 2) = |x2 – 2x + 5| + 2x ≥ x2 – 2x + 5 + 2x ≥ 5, ∀ x ∈ ℝ
Dấu bằng xảy ra tại x = 0. Suy ra min f (x, 2) = 5, ∀ x ∈ ℝ
Do đó ⇒ max (min f (x, m)) = 5, đạt được khi m = 2
Tổng quát: y = |ax2 + bx + c| + mx
Trường hợp 1: a․c > 0 ⇒ max (miny) = c
Đạt được khi m = -b
Câu 4. Giá trị nhỏ nhất của hàm số f (x, m) = |x2 – 4x – 7| đạt giá trị lớn nhất bằng
A. 7
B. -7
C. 0
D. 4
Hướng dẫn giải
Chọn C
Phương trình x2 – 4x – 7 luôn có hai nghiệm trái dấu x1 < 0 < x2
– Trường hợp 1: Nếu m ≥ 0
Ta có min f (x, m) ≤ f (x1, m) = mx1 ≤ 0, ∀ m ∈ ℝ
Xét m = 0 ta có f (x, 0) = |x2 – 4x – 7| ≥ 0, ∀ x ∈ ℝ
Dấu bằng xảy ra tại x = x1, 2. Suy ra min f (x, m) = 0, ∀ x ∈ ℝ
Do đó ⇒ max (min f (x, m)) = 0, đạt được khi m = 0
– Trường hợp 2: Nếu m < 0
Ta có min f (x, m) ≤ f (x2, m) = mx2 < 0, ∀ m ∈ ℝ ⇒ max (min f (x, m)) < 0
So sánh cả hai trường hợp thì max (min f (x, m)) = 0 khi m = 0
Trường hợp 2: a․c < 0 ⇒ max (miny) = 0
Đạt được khi m = 0
Dạng 5: Tìm giá trị lớn nhất giá trị nhỏ nhất khi cho đồ thị hoặc bảng biến thiên
Câu 1. Hàm số y = f(x) liên tục trên ℝ và có bảng biến thiên như hình bên dưới
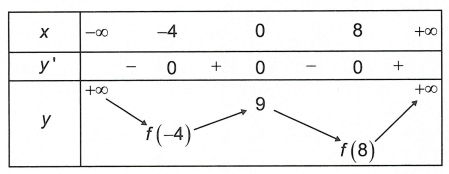
Biết f (-4) > f (8), khi đó giá trị nhỏ nhất của hàm số đã cho trên ℝ bằng
A. 9
B. f (-4)
C. f (8)
D. -4
Hướng dẫn giải
Chọn C
Từ bảng biến thiên ta có f(x) ≥ f (-4) ∀ m ∈ (-∞; 0] và f(x) ≥ f (8), ∀ m ∈ (0; +∞)
Mặt khác f (-4) > f (8) suy ra x ∈ (-∞; +∞) thì f(x) ≥ f (8)
Vậy
Câu 2. Cho hàm số y = f(x) xác định trên tập hợp và có bảng biến thiên như sau
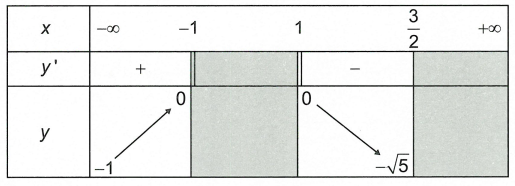
Khẳng định đúng là
A. ; không tồn tại
B. ;
C. ;
D. ; không tồn tại
Hướng dẫn giải
Chọn B
Dựa vào bảng biến thiên thì
Câu 3. Cho hàm số y = f(x) liên tục trên đoạn [-1; 3] và có đồ thị như hình vẽ bên dưới.
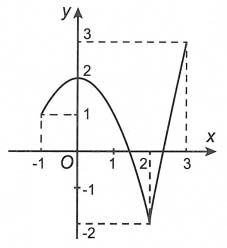
Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn [-1; 3]. Giá trị của M – m bằng
A. 1
B. 3
C. 4
D. 5
Hướng dẫn giải
Chọn D
Dựa vào đồ thị suy ra
M = f (3) = 3; m = f (2) = -2
Vậy M – m = 5
Câu 4. Cho đồ thị hàm số y = f’(x) như hình vẽ
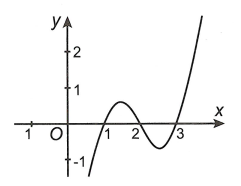
Hàm số y = f(x) đạt giá trị lớn nhất trên khoảng [1; 3] tại x0. Khi đó giá trị của x02 – 2x0 + 2019 bằng bao nhiêu?
A. 2018
B. 2019
C. 2021
D. 2022
Hướng dẫn giải
Chọn B
Dựa vào đồ thị của hàm số y = f’(x) ta có bảng biến thiên như sau
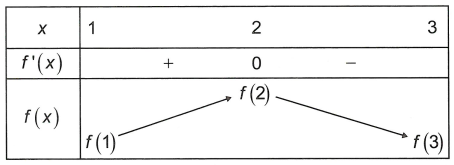
Dựa vào bảng biến thiên suy ra hàm số y = f(x) đạt giá trị lớn nhất trên khoảng [1; 3] tại x0 = 2
Vậy x02 – 2x0 + 2019 = 2019
Dạng 6. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số lượng giác
Phương pháp giải
Ghi nhớ: Điều kiện của các ẩn phụ
– Nếu ⇒ -1 ≤ t ≤ 1
– Nếu ⇒ 0 ≤ t ≤ 1
– Nếu ⇒ 0 ≤ t ≤ 1
Nếu t = sinx ± cosx =
- Bước 1. Đặt ẩn phụ và tìm điều kiện cho ẩn phụ
- Bước 2. Giải bài toán tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số theo ẩn phụ
- Bước 3. Kết luận (Chọn đáp án)
Bài tập vận dụng
Câu 1. Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y = 2cos2x + 2sinx là
A. ; m = -4
B. M = 4; m = 0
C. M = 0;
D. M = 4;
Hướng dẫn giải
Chọn A
Ta có y = 2cos2x + 2sinx = 2(1 – 2sin2x) + 2sinx = -4sin2x + 2sinx + 2
Đặt t = sin x, t ∈ [-1; 1], ta được y = -4t2 + 2t +2
Ta có y’ = 0 ⇔ -8t + 2 = 0 ⇔ t = ¼ ∈ (-1; 1)
Vì nên
; m = -4
Câu 2. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số bằng
A.
B.
C.
D. 3
Hướng dẫn giải
Chọn B
Đặt t = |cosx| ⇒ 0 ≤ t ≤ 1, ta được với 0 ≤ t ≤ 1
Vì , ∀ t ∈ [0; 1] nên
Suy ra tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho bằng
Câu 3. Giá trị lớn nhất M của hàm số là
A.
B. M = 3
C.
D.
Hướng dẫn giải
Chọn A
Đặt t = cos2x ⇒ 0 ≤ t ≤ 1, ta được với t ∈ [0; 1]
Ta có
Vì nên
Câu 4. Cho hàm số (với m là tham số thực). Giá trị lớn nhất của hàm số đạt giá trị nhỏ nhất khi m bằng
A.
B.
C.
D.
Hướng dẫn giải
Chọn A
Xét
Đặt t = sinx ⇒ -1 ≤ t ≤ 1, ta được với t ∈ [-1; 1]
Ta có
Vì nên
Hay
Mặt khác
Do đó
Dấu bằng đạt được khi
Câu 5. Giá trị nhỏ nhất của biểu thức P = |1 + 2cosx| + |1 + 2sinx| bằng
A.
B.
C. 1
D.
Hướng dẫn giải
Chọn B
Ta có P2 = 6 + 4(sinx + cosx) + 2|1 + 2(sinx + cosx) + 4sinx․cosx|
Đặt t = sinx + cosx = với
Xét y = P2 = 6 + 4t + 2 |2t2 + 2t – 1| =
Bảng biến thiên
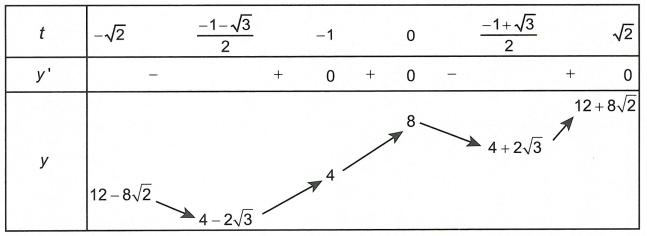
Dựa vào bảng biến thiên, suy ra
Câu 6. Giá trị lớn nhất của hàm số f(x) = sinx + cos2x trên đoạn [0; π] là
A.
B.
C.
D.
Hướng dẫn giải
Chọn D
Đặt t = sinx ⇒ cos2x = 1 – 2sin2x = 1 – 2t2 , với x ∈ [0; π] ⇒ t ∈ [0; 1]
Ta được f
Bạn đang xem bài viết Phân dạng và cách giải xem thêm các bài viết khác về chủ đề Toán lớp 12. Chúc bạn 1 ngày vui vẻ!