Toán lớp 12: Phương pháp tọa độ trong không gian mới nhất 2023

Bạn đang xem bài viết Phương pháp tọa độ trong không gian. Hi vọng sẽ là đáp án bạn ưng ý. Cùng theo dõi nhé!

Ở bài viết này, Cấp Nước Lào Cai sẽ giúp bạn đọc tổng hợp một số dạng bài tập sử dụng phương pháp tọa độ Oxyz trong chương trình toán lớp 12. Ở mỗi dạng toán đều sẽ có phương pháp giải và các ví dụ có lời giải chi tiết, từ đó giúp độc giả nắm bắt nội dung một cách nhanh chóng nhất.

Tóm tắt

Phần 1. Hệ trục tọa độ Oxyz

Dạng 1: Tọa độ của vectơ và các tính chất

Phương pháp giải

Định nghĩa:

Tính chất: Cho

+) cùng phương

Bài tập vận dụng

Câu 1. Trong không gian Oxyz, cho . Tọa độ vectơ là

Lời giải

Chọn B

Ta có:

Suy ra

Câu 2. Trong không gian với hệ tọa độ Oxyz, cho hai vectơ . Tọa độ vectơ thỏa mãn là

A. (–4; 2; –7)

B. (–4; 2; 3)

C. (–4; 12; –7)

D. (–4; 12; –3)

Lời giải

Chọn C

Ta có

Ta có:

Suy ra

Câu 3. Trong không gian với hệ tọa độ Oxyz, cho các vectơ .

Mệnh đề nào sau đây đúng?

Lời giải

Chọn C

Giả sử

Ta có hệ phương trình:

Giải hệ ta được:

Vậy

Dạng 2: Tìm tọa độ điểm

Phương pháp giải

Định nghĩa: (x: hoành độ, y: tung độ, z: cao độ)

Chú ý:

M ∈ (Oxy) ⇔ z = 0; M ∈ (Oyz) ⇔ x = 0; M ∈ (Oxz) ⇔ y = 0.

M ∈ Ox ⇔ y = z = 0; M ∈ Oy ⇔ x = z = 0; M ∈ Oz ⇔ x = y = 0.

Tính chất: Cho A(x_A; y_A; z_A), B(x_B; y_B; z_B)

Tọa độ trung điểm M của đoạn thẳng AB:

Toạ độ trọng tâm G của tam giác ABC:

Toạ độ trọng tâm G của tứ diện ABCD:

Bài tập vận dụng

Câu 1. Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(1; –3; 2), B(0; 1; –1) và C(5; –1; 2). Tọa độ là trọng tâm G của tam giác ABC là

A. G(2; –1; 1)

B. G(2; 1 ;1)

C. G(2; 1; –1)

D. G(–2; 1; –1)

Lời giải

Chọn A

G là trọng tâm tam giác ABC nên:

Vậy G(2; –1; 1)

Câu 2. Trong không gian với hệ tọa độ Oxyz, cho 3 điểm A(1; 0; –2), B(2; 1; –1) và C(1; –3; 3) và điểm M thỏa mãn hệ thức . Tìm tọa độ điểm M .

A. (0; –5; –6)

B. (0; –5; 2)

C. (0; –10; 12)

D. (0; –5; 4)

Lời giải

Chọn C

Ta có:

Gọi

Vậy M(0; –10; 12)

Dạng 3: Tích vô hướng, tích có hướng của hai vectơ

Phương pháp giải

1. Định nghĩa

Trong không gian Oxyz cho hai vectơ

+) Tích vô hướng của hai vectơ:

+) Tích có hướng của hai vectơ và , kí hiệu là , được xác định bởi

2. Chú ý

Tích có hướng của hai vectơ là một vectơ, tích vô hướng của hai vectơ là một số.

3. Tính chất

+) cùng phương

5. Ứng dụng của tích có hướng

+) Điều kiện đồng phẳng của ba vectơ: và đồng phẳng

+) Diện tích hình bình hành ABCD:

+) Diện tích tam giác ABC:

+) Thể tích khối hộp ABCDA’B’C’D’:

+) Thể tích tứ diện ABCD:

+) Góc giữa hai vectơ:

Bài tập vận dụng

Câu 1. Trong không gian Oxyz, cho . Phát biểu nào sau đây sai?

Lời giải

Chọn D

Ta có: không vuông góc nhau.

Câu 2. Trong không gian Oxyz, cho . Tìm tham số m để

A. m = 2

B. m = –2

C. m = 0

D. m = –1

Lời giải

Chọn B

Ta có:

Phần 2. Các bài toán về phương trình mặt cầu

Dạng 1. Xác định tọa độ tâm và bán kính mặt cầu. Nhận biết phương trình mặt cầu

Phương pháp giải

Dạng chính tắc: (x – a)² + (y – b)² + (z – c)² = R², có tâm I(a; b; c), bán kính R

Dạng khai triển: x² + y² + z² – 2ax – 2by – 2cz + d = 0 (a² + b² + c² – d > 0), có tâm I(a; b; c), bán kính

Bài tập vận dụng

Câu 1. Trong không gian với hệ tọa độ Oxyz, tọa độ tâm I và bán kính R của mặt cầu có phương trình (x + 2)² + (y – 3)² + z² = 5 là:

Lời giải

Chọn B

Mặt cầu có tâm I(–2; 3; 0) và bán kính là

Câu 2. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): x² + y² + z² – 2x + 4y – 4z – 25 = 0. Tìm tọa độ tâm I và bán kính mặt cầu (S).

Lời giải

Chọn A

Từ phương trình ta có: a = 1, b = –2, c = 2, d = –25

Suy ra (S) tâm I(1; –2; 2);

Câu 3. Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S) có phương trình (S): x² + y² + z² – 2x – 4y – 6z + 5 = 0. Tính diện tích mặt cầu (S).

A. 42π

B. 36π

C. 9π

D. 12π

Lời giải

Chọn B

Mặt cầu (S) có tâm I(1; 2; 3) và bán kính

Diện tích mặt cầu (S): S = 4πR² = 4π3² = 36π

Dạng 2. Lập phương trình mặt cầu khi biết một số yếu tố cho trước

Phương pháp giải

Xác định được tâm và bán kính, hoặc là các hệ số a,b, c, d

Mặt cầu có tâm I(a; b; c), bán kính R thì có phương trình chính tắc là:

(x – a)² + (y – b)² + (z – c)² = R²

Mặt cầu có tâm I(a; b; c) và đi qua điểm A

+) Tính bán kính

+) Viết phương trình mặt cầu.

Mặt cầu có đường kính AB

+) Tìm tọa độ tâm I (trung điểm của đoạn AB)

+) Tính bán kính

+) Viết phương trình mặt cầu.

Mặt cầu ngoại tiếp tứ diện ABCD (hoặc là: Mặt cầu đi qua 4 điểm A, B, C, D có tọa độ cho trước)

+) Gọi mặt cầu (S): x² + y² + z² – 2ax – 2by – 2cz + d = 0 (a² + b² + c² – d > 0)

+) Thay tọa độ các điểm A, B, C, D vào phương trình mặt cầu, lập được hệ 4 phương trình 4 ẩn a, b, c, d

+) Kết luận phương trình cần lập.

Mặt cầu có tâm I(a; b; c) và tiếp xúc với mặt phẳng (P): Ax + By + Cz + D = 0

+) Tính bán kính

+) Viết phương trình mặt cầu: (x – a)² + (y – b)² + (z – c)² = R²

Mặt cầu có tâm I(a; b; c) và tiếp xúc với đường thẳng (∆):

+) Xác đinh tọa độ điểm M(x₀; y₀; z₀) và vectơ chỉ phương của đường thẳng (∆)

+) Tính bán kính

+) Viết phương trình mặt cầu.

Bài tập vận dụng

Câu 1. Trong không gian với hệ tọa độ Oxyz cho mặt cầu (S) có tâm I(–1; 4; 2) và bán kính R = 9. Phương trình của mặt cầu (S) là:

A. (x + 1)² + (y – 4)² + (z – 2)² = 81

B. (x + 1)² + (y – 4)² + (z – 2)² = 9

C. (x – 1)² + (y + 4)² + (z – 2)² = 9

D. (x – 1)² + (y + 4)² + (z + 2)² = 81

Lời giải

Chọn A

Mặt cầu (S) có tâm I(–1; 4; 2) và bán kính R = 9 nên (S) có phương trình:

(x + 1)² + (y – 4)² + (z – 2)² = 81

Câu 2. Trong không gian Oxyz, phương trình mặt cầu tâm I(–1; 2; 0) và đi qua điểm A(2; –2; 0) là

A. (x + 1)² + (y – 2)² + z² = 100

B. (x + 1)² + (y – 2)² + z² = 5

C. (x + 1)² + (y – 2)² + z² = 10

D. (x + 1)² + (y – 2)² + z² = 25

Lời giải

Chọn D

Ta có: Tâm I(–1; 2; 0) và bán kính

Vậy phương trình mặt cầu có dạng: (x + 1)² + (y – 2)² + z² = 25

Câu 3. Trong không gian Oxyz, cho hai điểm A(–2; 1; 0), B(2; –1; 2). Phương trình của mặt cầu có đường kính AB là

A. x² + y² + (z – 1)² = 12

B. x² + y² + (z – 1)² = 36

C. x² + y² + (z – 1)² = 24

D. x² + y² + (z – 1)² = 6

Lời giải

Chọn D

Gọi I là trung điểm của AB khi đó

Mặt cầu đường kính AB nhận điểm I(0; 0; 1) làm tâm và bán kính có phương trình là: x² + y² + (z – 1)² = 6

Câu 4. Gọi (S) là mặt cầu đi qua 4 điểm A(2; 0; 0), B(1; 3; 0), C(–1; 0; 3), D(1; 2; 3). Tính bán kính R của (S)

B. R = 3

C. R = 6

Lời giải

Chọn D

Giả sử phương trình mặt cầu (S): x² + y² + z² – 2ax – 2by – 2cz + d = 0 (a² + b² + c² – d > 0)

Vì (S) đi qua 4 điểm A(2; 0; 0), B(1; 3; 0), C(–1; 0; 3), D(1; 2; 3) nên ta có hệ phương trình:

Câu 5. Trong không gian Oxyz cho điểm I(–1; 2; 3) và mặt phẳng (P): 4x + y – z – 1 = 0. Viết phương trình mặt cầu tâm I và tiếp xúc với mặt phẳng (P).

A. (x + 1)² + (y – 2)² + (z – 3)² = 2

B. (x + 1)² + (y – 2)² + (z – 3)² = 4

C. (x – 1)² + (y + 2)² + (z + 3)² = 2

D. (x + 1)² + (y – 2)² + (z – 3)² = 1

Lời giải

Chọn A

Gọi (S) là mặt cầu tâm I, bán kính R và (S) tiếp xúc với (P): 4x + y – z – 1 = 0

Ta có

Vậy mặt cầu (S) có phương trình: (x + 1)² + (y – 2)² + (z – 3)² = 2

Phần 3. Phương trình mặt phẳng

Dạng 1: Tìm một VTPT của mặt phẳng

Phương pháp:

Định nghĩa: Vectơ , có giá vuông góc với (P) ⇒ là 1 VTPT của (P)

Chú ý:

+) Nếu là một VTPT của mặt phẳng (P) thì cũng là một VTPT của mp (P)

+) Nếu mp (P) có phương trình Ax + By + Cz + D = 0 thì nó có một VTPT là

+) Nếu (P) có cặp không cùng phương với nhau và có giá song song hoặc nằm trên mặt phẳng (P) thì là một VTPT của (P).

Ví dụ minh họa

Ví dụ 1. Trong không gian Oxyz, cho mặt phẳng (α): 3x + 2y – 4z + 1 = 0. Vectơ nào sau đây là một vectơ pháp tuyến của mặt phẳng (α)?

Lời giải

Chọn D

Phương trình mặt phẳng (α) có dạng:

Ax + By + Cz + D = 0 với A = 3, B = 2, C = –4, D = 1

Suy ra (α) có là một vecto pháp tuyến của mặt phẳng (α).

Ví dụ 2. Trong không gian với hệ toạ độ Oxyz, cho mặt phẳng (P): 2x – 3z + 4 = 0. Vectơ nào dưới đây có giá vuông góc với mặt phẳng (P)?

Lời giải

Chọn B

Vectơ có giá vuông góc với mặt phẳng (P) vì là một vectơ pháp tuyến của (P).

Ví dụ 3. Trong không gian Oxyz, cho ba điểm A(2; –1; 3), B(4; 0; 1) và C(–10; 5; 3). Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng (ABC)?

Lời giải

Chọn A

Ta có:

⇒ (ABC) có một vectơ pháp tuyến là

Dạng 2: Viết phương trình mặt phẳng

Phương pháp:

Viết phương trình mặt phẳng khi biết một điểm và vectơ pháp tuyến của nó.

+) Mặt phẳng (α) đi qua điểm M(x₀; y₀; z₀) và nhận vectơ làm VTPT có phương trình dạng (α): A(x – x₀) + B(y – y₀) + C(z – z₀) = 0 hay (α): Ax + By + Cz + D = 0

+) Mặt phẳng (α) đi qua điểm ba điểm A(a; 0; 0), B(0; b; 0), C(0; 0; c) có phương trình theo đoạn chắn:

Viết phương trình mặt phẳng (α) đi qua 1 điểm M(x₀; y₀; z₀) và song song với 1 mặt phẳng (β): Ax + By + Cz + D = 0 cho trước.

+) VTPT của (β) là

+) Vì (α) // (β) nên VTPT của mặt phẳng (α) là

+) Phương trình mặt phẳng (α): A(x – x₀) + B(y – y₀) + C(z – z₀) = 0

Viết phương trình mặt phẳng (α) đi qua 3 điểm A, B, C không thẳng hàng.

+) Tìm tọa độ các vectơ:

+) Vectơ pháp tuyến của (α) là:

+) Điểm thuộc mặt phẳng là A (hoặc B hoặc C)

+) Viết phương trình mặt phẳng qua 1 điểm và có VTPT

Viết phương trình mặt phẳng (α) qua hai điểm A, B và vuông góc với mặt phẳng (β)

+) Tìm VTPT của (β) là

+) Tìm tọa độ vectơ

+) VTPT của mặt phẳng (α) là

+) Áp dụng cách viết phương trình mặt phẳng đi qua 1 điểm và có 1 VTPT.

Bài tập minh họa

Ví dụ 1. Trong không gian với hệ tọa độ mặt phẳng Oxyz, phương trình nào được cho dưới đây là phương trình mặt phẳng (Oyz)?

A. x = y + z

B. y – z = 0

C. y + z = 0

D. x = 0

Lời giải

Chọn D

Mặt phẳng (Oyz) đi qua O(0; 0; 0) và nhận làm vectơ pháp tuyến nên phương trình mặt phẳng (Oyz) là x = 0

Ví dụ 2. Trong không gian Oxyz, cho hai điểm A(1; 5; –2), B(3; 1; 2). Viết phương trình mặt phẳng trung trực của đoạn thẳng AB.

A. 2x + 3y + 4 = 0

B. x – 2y + 2z = 0

C. x – 2y + 2z + 8 = 0

D. x – 2y + 2z + 4 = 0

Lời giải

Chọn D

Ta có: là một VTPT của mặt phẳng trung trực đoạn thẳng AB.

Gọi I là trung điểm của AB ⇒ I(2; 3; 0).

Mặt phẳng trung trực của đoạn thẳng AB đi qua điểm I và có VTPT nên có phương trình là: 2(x – 2) – 4(y – 3) + 4(z – 0) = 0 ⇔ x – 2y + 2z + 4 = 0

Ví dụ 3. Trong không gian Oxyz, mặt phẳng chứa trục Oz và vuông góc với mặt phẳng (α): x – y + 2z – 1 = 0 có phương trình là

A. x + y = 0

B. x + 2y = 0

C. x – y = 0

D. x+ y – 1 = 0

Lời giải

Chọn A

Mặt phẳng (α): x – y + 2z – 1 = 0 có vectơ pháp tuyến

Trên trục Oz có vectơ đơn vị

Mặt phẳng chứa trục Oz và vuông góc với mặt phẳng (α) là mặt phẳng qua O và nhận làm vectơ pháp tuyến.

Do đó có phương trình –x – y = 0 ⇔ x + y = 0

Dạng 3: Điểm thuộc mặt phẳng

Phương pháp

Điểm M(x₀; y₀; z₀) ∈ (P): Ax + By + Cz + D = 0 ⇔ Ax₀ + By₀ + Cz₀ + D = 0

Ví dụ minh họa

Ví dụ 1. Trong không gian Oxyz, điểm nào dưới đây nằm trên mặt phẳng (P): 2x – y + z – 2 = 0?

A. Q(1; –2; 2)

B. P(2; –1; –1)

C. M(1; 1; –1)

D. N(1; –1; –1)

Lời giải

Chọn D

Thay toạ độ điểm Q vào phương trình mặt phẳng (P) ta được 2.1 – (–2) + 2 – 2 = 4 ≠ 0 nên Q ∉ (P)

Thay toạ độ điểm P vào phương trình mặt phẳng (P) ta được 2.2 – (–1) + (–1) – 2 = 2 ≠ 0 nên P ∉ (P)

Thay toạ độ điểm M vào phương trình mặt phẳng (P) ta được 2.1 – 1 + (–1) – 2 = –2 ≠ 0 nên M ∉ (P)

Thay toạ độ điểm N vào phương trình mặt phẳng (P) ta được 2.1 – (–1) + (–1) – 2 = 0 nên N ∈ (P)

Ví dụ 2. Trong không gian Oxyz, gọi d là giao tuyến của hai mặt phẳng (α): 2x – y + 3z – 7 = 0 và (β): x – 2y + z – 2 = 0. Đường thẳng d đi qua điểm nào dưới đây?

A. Q(2; –1; 3)

B. M(1 ; 0; –3)

C. P(–1; 0; 3)

D. N(1; –2; 1)

Lời giải

Chọn C

Điểm

Phần 4. Phương trình đường thẳng

Dạng 1: Tìm một VTCP của đường thẳng

Phương pháp

Định nghĩa: Vectơ , có giá song song hoặc trùng với d ⇒ là 1 VTCP của đường thẳng d.

Chú ý:

Nếu là một VTCP của đường thẳng d thì là một VTCP của đường thẳng d

+) Nếu ∆ có trình tham số của dạng: thì ∆ có 1 VTCP là

+) Nếu a₁a₂a₃ ≠ 0 thì được gọi là phương trình chính tắc.

+) Nếu ∆ có giá song song hoặc nằm trên mặt phẳng (P) và vuông góc với đường thẳng d thì ∆ có 1 VTCP là

Ví dụ minh họa

Ví dụ 1. Trong không gian Oxyz cho đường thẳng ∆ song song với đường thẳng d: . Một vectơ chỉ phương của ∆ là

Lời giải

Chọn A

Theo phương trình tham số của đường thẳng ∆ thì ta thấy có một vectơ chỉ phương là

Ví dụ 2. Trong không gian Oxyz, vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng d: ?

A. (2; –1; 3)

B. (2; 1; 3)

C. (1; –2; 0)

D. (1; 2; 0)

Lời giải

Chọn A

Theo phương trình chính tắc của đường thẳng d thì ta thấy d có một vectơ chỉ phương là (2; –1; 3)

Ví dụ 3. Trong không gian Oxyz, cho đường thẳng d song song với trục Oy. Đường thẳng d có một vectơ chỉ phương là

Lời giải

Chọn B

Vì đường thẳng d song song với trục Oy nên vectơ chỉ phương của d cùng phương với vectơ đơn vị

Vậy đường thẳng d có một vectơ chỉ phương là

Ví dụ 4. Trong không gian Oxyz, đường thẳng qua hai điểm M(–2; 1; 2), N(3; –1; 0) có một vectơ chỉ phương là

Lời giải

Chọn B

Đường thẳng đi qua hai điểm M(–2; 1; 2) và N(3; –1; 0) nhận làm một VTCP

Vậy cũng là một VTCP của đường thẳng đã cho.

Dạng 2: Viết phương trình của đường thẳng

Phương pháp:

Xác định một điểm cố định M(x₀; y₀; z₀) thuộc ∆

Xác định một vectơ chỉ phương của ∆

Viết phương trình đường thẳng:

+) Phương trình tham số của ∆ có dạng:

+) Phương trình chính tắc của ∆ có dạng:

Ví dụ minh họa

Ví dụ 1. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: . Phương trình chính tắc của d là

Lời giải

Chọn D

Ta có:

Do đó phương trình chính tắc của d là:

Ví dụ 2. Trong không gian với hệ tọa độ Oxyz, trục Ox có phương trình tham số là

Lời giải

Chọn B

Trục Ox đi qua O(0; 0; 0) và nhận làm vectơ chỉ phương nên có phương trình tham số là

Ví dụ 3. Trong không gian Oxyz, phương trình chính tắc của đường thẳng đi qua điểm M(2; –1; 3) và có vectơ chỉ phương là

Lời giải

Chọn D

Phương trình chính tắc của đường thẳng đi qua điểm M(x₀; y₀; z₀) và có vectơ chỉ phương với a.b.c ≠ 0 là nên phương trình đường thẳng cần tìm là

Ví dụ 4. Cho điểm A(1; 2; 3) và hai mặt phẳng (P): 2x + 2y + z + 1 = 0, (Q): 2x – y + 2z – 1 = 0. Phương trình đường thẳng d đi qua A song song với cả (P) và (Q) là

Lời giải

Chọn D

Ta có (P): 2x + 2y + z + 1 = 0 có một vectơ pháp tuyến là

(Q): 2x – y + 2z – 1 = 0 có một vectơ pháp tuyến là

Đường thẳng d có một vectơ chỉ phương là

Do đường thẳng d song song với (P) và (Q)

Nên

Mặt khác đường thẳng d đi qua A(1; 2; 3) và có vectơ chỉ phương nên phương trình chính tắc của d là

Dạng 3: Tìm điểm thuộc đường thẳng và giao điểm của đường thẳng và mặt phẳng

Phương pháp

Phương trình tham số của d:

Điểm M ∈ d ⇔ M(x₀ + a₁t; y₀ + a₂t; z₀ + a₃t)

M ∈ (P) ⇔ A(x₀ + at) + B(y₀ + bt) + C(z₀ + ct) + D = 0

Từ đó suy ra t rồi suy ra tọa độ giao điểm M.

Ví dụ minh họa

Ví dụ 1. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d:

Điểm nào sau đây không thuộc đường thẳng d .

A. M(1; –1; –5)

B. M(1; –1; 3)

C. M(3; –2; –1)

D. M(5; –3; 3)

Lời giải

Chọn B

Thử đáp án A ta được: . Suy ra M thuộc đường thẳng d.

Thử đáp án B ta được: . Suy ra M không thuộc đường thẳng d.

Thử đáp án C ta được: . Suy ra M thuộc đường thẳng d.

Thử đáp án D ta được: . Suy ra M thuộc đường thẳng d.

Ví dụ 2. Trong không gian Oxyz, cho đường thẳng d: và mặt phẳng (P): x + 2y – z – 5 = 0. Tọa độ giao điểm của d và (P) là

A. (2; 1; –1)

B. (3; –1; –2)

C. (1; 3; –2)

D. (1; 3; 2)

Lời giải

Chọn D

Xét hệ:

⇔ t = 1 ⇒ A(1; 3; 2) là tọa độ giao điểm của đường thẳng và mặt phẳng.

Ví dụ 3. Trong không gian Oxyz, giao điểm của đường thẳng d: và mặt phẳng (P): 2x – y – z – 7 = 0 có tọa độ là

A. (3; –1; 0)

B. (0; 2; –4)

C. (6; –4; 3)

D. (1; 4; –2)

Lời giải

Chọn A

Phương trình tham số của d:

Tọa độ giao điểm của d và (P) là nghiệm của hệ:

Vậy tọa độ giao điểm cần tìm là (3; –1; 0)

Phần 5. Vị trí tương đối tổng hợp

Dạng 1. Vị trí tương đối giữa 2 mặt phẳng

Phương pháp

Cho 2 mặt phẳng (P): A₁x + B₁y + C₁z + D₁ = 0 và (Q): A₂x + B₂y + C₂z + D₂ = 0

(P) có VTPT và (Q) có VTPT

+) Nếu thì (P) // (Q)

+) Nếu thì (P) ≡ (Q)

+) Nếu và không cùng phương thì (P), (Q)

+) Nếu thì (P) ⊥ (Q)

Ví dụ minh họa

Ví dụ 1. Trong không gian với hệ tọa độ Oxyz cho mặt phẳng (P): x – 2y + z – 1 = 0 và mặt phẳng (Q): 3x – 3y + 2z + 6 = 0. Mệnh đề nào dưới đây đúng?

A. (Q) cắt và không vuông góc với (P)

B. (Q) ⊥ (P)

C. (Q) song song với (P)

D. (Q) ≡ (P)

Lời giải

Chọn A

Ta có: ⇒ (P) và (Q) cắt nhau

Xét

⇒ (P) và (Q) cắt và không vuông góc nhau.

Ví dụ 2. Trong không gian với hệ tọa độ Oxyz cho mặt phẳng (P): 2x + 4y – 6z + 5 = 0 và mặt phẳng (Q): x + 2y + mz + 1 = 0. Tìm m để hai mặt phẳng (P) và (Q) song song

A. m = 3

B. m = –3

C. m = 2

D. m = –2

Lời giải

Chọn B

(P) có VTPT

(Q) có VTPT

Để 2 mặt phẳng song song thì cùng phương.

Ví dụ 3. Trong không gian với hệ tọa độ Oxyz cho mặt phẳng (P): 5x – 2y + z – 1 = 0 và mặt phẳng (Q): x – 3y + mz + 11 = 0. Tìm m để hai mặt phẳng (P) và (Q) vuông góc nhau.

A. m = –11

B. m = 1

C. m = 11

D. m = –1

Lời giải

Chọn A

(P) có VTPT

(Q) có VTPT

Để 2 mp vuông góc nhau thì

Dạng 2. Vị trí tương đối giữa mặt phẳng và đường thẳng

Phương pháp

Cho đường thẳng d qua điểm M(x₀; y₀; z₀) có vectơ chỉ phương và mặt phẳng (P): Ax + By + Cz + D = 0 có vectơ pháp tuyến

+) d // (P) nếu và không có điểm chung.

+) d ⊂ (P) nếu và có điểm chung.

+) d ⊥ (P) nếu

Sơ đồ tư duy:

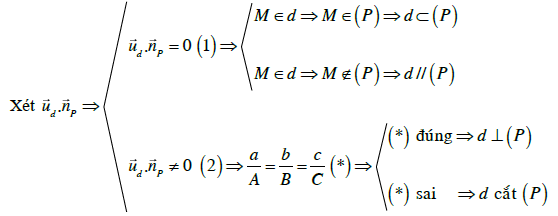
Cho đường thẳng d: và mặt phẳng (P): Ax + By + Cz + D = 0

Xét phương trình (P): A(x₀ + a₁t) + B(y₀ + a₂t) + C(z₀ + a₃t) + D = 0

+) Nếu pt (1) vô nghiệm thì d // (P)

+) Nếu pt (1) vô số nghiệm thì d ⊂ (P)

+) Nếu pt (1) có nghiệm thì t = t₀ thì d cắt (P) tại điểm M(x₀ + a₁t; y₀ + a₂t; z₀ + a₃t)

Ví dụ minh họa

Ví dụ 1. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: và mặt phẳng (P): 3x – 3y + 2z + 6 = 0. Mệnh đề nào dưới đây đúng?

A. d cắt và không vuông góc với (P)

B. d vuông góc với (P)

C. d song song với (P)

D. d nằm trong (P)

Lời giải

Chọn A

Đường thẳng d đi qua M(–1; 0; 5) có VTCP và mặt phẳng (P) có VTPT

Vì , suy ra d cắt hoặc vuông góc với (P)

Vì ⇒ không cùng phương ⇒ không vuông góc.

Vậy d cắt và không vuông góc với (P)

Ví dụ 2. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng ∆ có phương trình: . Xét mặt phẳng (P): 10x + 2y + mz + 11 = 0, m là tham số thực. Tìm tất cả các giá trị của m để mặt phẳng (P) vuông góc với đường thẳng ∆.

A. m = –2

B. m = 2

C. m = –52

D. m = 52

Lời giải

Chọn B

Đường thẳng ∆: có vectơ chỉ phương

Mặt phẳng (P): 10x + 2y + mz + 11 = 0 có vectơ pháp tuyến

Để mặt phẳng (P) vuông góc với đường thẳng ∆ thì phải cùng phương với

Dạng 3. Vị trí tương đối giữa đường thẳng và đường thẳng

Phương pháp

Cho đường thẳng d₁ qua điểm M(x₁; y₁; z₁), có vectơ chỉ phương và d₂ qua điểm M’(x₂; y₂; z₂), có vectơ chỉ phương

+) d₁ // d₂ nếu và không có điểm chung.

+) d₁ ≡ d₂ nếu và có một điểm chung.

+) d₁ cắt d₂ nếu không song song và

+) d₁ chéo d₂ nếu không song song và

Sơ đồ tư duy:

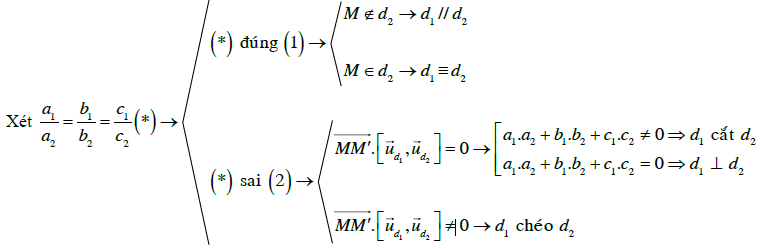
Ví dụ minh họa

Ví dụ 1. Trong không gian với hệ tọa độ Oxyz, vị trí tương đối của đường thẳng d₁: và đường thẳng d₂: là

A. Cắt nhau

B. Song song

C. Chéo nhau

D. Trùng nhau.

Lời giải

Chọn A

d₁ qua M₁(–1; 1; –1), có vectơ chỉ phương

d₂ qua M₂(–3; –2; –2), có vectơ chỉ phương

không cùng phương

Ta có:

⇒ d₁ cắt d₂

Ví dụ 2. Trong không gian với hệ tọa độ Oxyz, vị trí tương đối của d₁: và d₂: là

A. Trùng nhau

B. Cắt nhau

C. Song song

D. Chéo nhau.

Lời giải

Chọn D

d₁ qua M₁(0; 0; 4), có vectơ chỉ phương

d₂ qua M₂(3; 0; 0), có vectơ chỉ phương

không cùng phương

Ta có:

⇒ d₁ chéo d₂

Dạng 4. Vị trí tương đối mặt cầu và mặt phẳng

Phương pháp

Cho mặt cầu (S): (x – a)² + (y – b)² + (z – c)² = R² tâm I(a; b; c) bán kính R và mặt phẳng (P): Ax + By + Cz + D = 0

+) Nếu d(I, (P)) > R thì mp (P) và mặt cầu (S) không có điểm chung.

+) Nếu d(I, (P)) = R thì mặt phẳng (P) và mặt cầu (S) tiếp xúc nhau.

Khi đó (P) gọi là tiếp diện của mặt cầu (S) và điểm chung gọi là tiếp điểm.

+) Nếu d(I, (P)) < R thì mặt phẳng (P) và mặt cầu (S) cắt nhau theo giao tuyến là đường tròn có phương trình:

Trong đó bán kính đường tròn và tâm H của đường tròn là hình chiếu của tâm I mặt cầu (S) lên mặt phẳng (P).

Ví dụ minh họa

Ví dụ 1. Trong không gian với hệ tọa độ Oxyz cho mặt phẳng (P): x – 2y + z – 1 = 0 và mặt cầu (S): (x – 1)² + (y – 2)² + (z + 1)² = 4. Mệnh đề nào dưới đây đúng?

A. (P) không cắt (S)

B. (P) tiếp xúc (S)

C. (P) cắt (S)

D. (P) đi qua tâm của (S)

Lời giải

Chọn A

(S) có tâm I(1; 2; –1) và bán kính R = 2

Khoảng cách từ tâm I đến (P):

Vậy (P) không cắt (S).

Ví dụ 2. Trong không gian với hệ tọa độ Oxyz cho mặt phẳng (P): x + 3y + 4z + m = 0 và mặt cầu (S): (x – 1)² + (y – 2)² + (z – 3)² = 26. Xác định m để (P) tiếp xúc với (S)?

A. m = 7, m = –45

B. m = 7, m = 45

C. m = –7, m = 45

D. m = –7, m = –45

Lời giải

Chọn A

(S) có tâm I(1; 2; 3) và bán kính

(P) tiếp xúc với (S)

Ví dụ 3. Trong không gian với hệ tọa độ Oxyz, cho điểm I(1; 0; –2) và mặt phẳng (P) có phương trình: x + 2y – 2z + 4 = 0. Phương trình mặt cầu (S) có tâm I và tiếp xúc với (P) là

A. (x – 1)² + y² + (z + 2)² = 9

B. (x – 1)² + y² + (z + 2)² = 3

C. (x + 1)² + y² + (z – 2)² = 3

D. (x + 1)² + y² + (z – 2)² = 9

Lời giải

Chọn A

Ta có

Phương trình mặt cầu (S) có tâm I(1; 0; –2), bán kính R = 3 có dạng (S): (x – 1)² + y² + (z + 2)² = 9

Dạng 5. Vị trí tương đối mặt cầu và đường thẳng

Phương pháp

Cho đường thẳng d: qua M₀(x₀; y₀; z₀) và có vectơ chỉ phương

Mặt cầu (S): (x – a)² + (y – b)² + (z – c)² = R² có tâm I(a; b; c), bán kính R .

Gọi khoảng cách từ tâm I của mặt cầu (S) đến đường thẳng d là

+) Nếu d(I, d) > R thì d không cắt (S)

+) Nếu d(I, d) = R thì d tiếp xúc (S)

+) Nếu d(I, d) < R thì d cắt (S) tại hai điểm phân biệt A, B và AB vuông góc với đường kính (bán kính) mặt cầu. Khi đó

Ví dụ minh họa

Ví dụ 1. Trong không gian với hệ tọa độ Oxyz, đường thẳng d: và mặt cầu (S): x² + y² + z² – 2x + 4z + 1 = 0. Số điểm chung của d và (S) là

A. 3

B. 0

C. 2

D. 1

Lời giải

Chọn B

d qua M(0; 1; 2), có vectơ chỉ phương

(S) có tâm I(1; 0; –2) và

Vậy d và (S) không cắt nhau.

Ví dụ 2. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: , mặt cầu tâm I(2; 5; 3) tiếp xúc với d là

A. (S): (x – 2)² + (y – 5)² + (z – 3)² = 18

B. (S): (x – 2)² + (y – 5)² + (z – 3)² = 16

C. (S): (x – 2)² + (y – 5)² + (z – 3)² = 25

D. (S): (x – 2)² + (y – 5)² + (z – 3)² = 9

Lời giải

Chọn A

d qua M(1; 0; 2), có vectơ chỉ phương

Mặt cầu tiếp xúc với đường thẳng nên

⇒ R² = 18

Phần 6. Các bài toán về khoảng cách

Dạng 1. Khoảng cách giữa hai điểm

Phương pháp

Cho hai điểm A(x₁; y₁; z₁), B(x₂; y₂; z₂)

Ví dụ minh họa

Ví dụ 1. Trong không gian với hệ trục toạ độ Oxyz, cho điểm A(2; 2; 1). Tính độ dài đoạn thẳng OA.

A. OA = 3

B. OA = 9

C. OA = 25

D. OA = 5

Lời giải

Chọn A

Ví dụ 2. Trong không gian Oxyz, cho hai điểm A(4; 3; –2) và B(3; –5; 0). Độ dài đoạn thẳng AB là

D. 4

Lời giải

Chọn A

Với A(4; 3; –2) và B(3; –5; 0) thì , do đó

Ví dụ 3. Trong không gian với hệ tọa độ Oxyz, cho các điểm A(3; –4; 0), B(–1; 1; 3), C(3; 1; 0). Tìm tọa độ điểm D trên trục hoành sao cho AD = BC.

A. D(–2; 1; 0), D(–4; 0; 0)

B. D(0; 0; 0), D(–6; 0; 0)

C. D(6; 0; 0), D(12; 0; 0)

D. D(0; 0; 0), D(6; 0; 0)

Lời giải

Chọn D

Gọi D(x; 0; 0) ∈ Ox

Dạng 2. Khoảng cách từ điểm đến mặt phẳng, khoảng cách giữa hai mặt phẳng song song, khoảng cách giữa một đường thẳng song song với mặt phẳng tới mặt phẳng.

Phương pháp:

Trong không gian Oxyz, cho điểm M₀(x₀; y₀; z₀) và mặt phẳng (α): Ax + By + Cz + D = 0. Khi đó khoảng cách từ điểm M₀ đến mặt phẳng (α) được tính:

Đặc biệt: d(M, (Oxy)) = |z₀|; d(M, (Oxz)) = |y₀|; d(M, (Oyz)) = |x₀|

Khoảng cách giữa hai mp song song là khoảng cách từ một điểm thuộc mặt phẳng này đến mặt phẳng kia.

Chú ý: Nếu hai mặt phẳng không song song thì khoảng cách giữa chúng bằng 0.

Khoảng cách giữa đường thẳng song song với mặt phẳng tới mặt phẳng là khoảng cách từ một điểm thuộc đường thẳng đến mặt phẳng.

Chú ý: Nếu đường thẳng không song song với mặt phẳng thì khoảng cách giữa chúng bằng 0.

Ví dụ minh họa

Ví dụ 1. Trong không gian với hệ tọa độ Oxyz, cho điểm M(2; –3; 5) và mặt phẳng (α) có phương trình: 2x – y + 2z – 6 = 0. Khoảng cách từ điểm M mặt phẳng (α) là

Lời giải

Chọn B

Áp dụng công thức

Ví dụ 2. Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (α): 2x + 3y – z + 2 = 0, (β): 2x + 3y – z + 16 = 0. Khoảng cách giữa hai mặt phẳng (α) và (β) là