Toán lớp 12: Tỉ số thể tích – Kỹ thuật chuyển đỉnh và các bài tập vận dụng mới nhất 2023

Ở bài viết này, Cấp Nước Lào Cai sẽ giúp bạn đọc tổng hợp các kỹ thuật chuyển đỉnh trong hình học và ứng dụng tỉ số thể tích để giải các bài toán hình học không gian từ dễ tới khó.

Lý thuyết tỉ số thể tích khối đa diện

Chúng ta cần tìm hiểu một vài kỹ thuật chuyển đỉnh để ứng dụng vào các bài toán như sau:

1. Song song đáy

V_cũ = V_mới

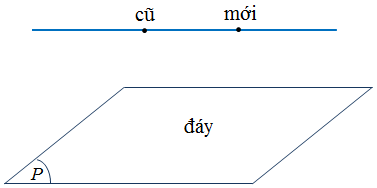
2. Cắt đáy

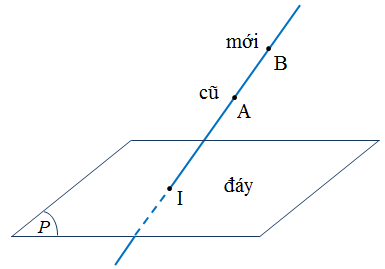
4. Kỹ thuật chuyển đáy (đường cao không đổi)

Để kỹ thuật chuyển đáy được thuận lợi, ta nên chọn hai đáy có cùng công thức tính diện tích, khi đó ta sẽ dễ dàng so sánh tỉ số hơn.

Cả hai kỹ thuật đều nhằm mục đích chuyển đa diện ban đầu về đa diện khác dễ tính thể tích hơn.

5. Tỉ số diện tích của hai tam giác

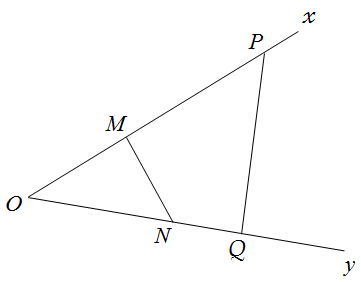
Tỉ số thể tích của khối chop

Công thức tỉ số thể tích của hình chóp tam giác

Công thức trên chỉ áp dụng cho hình chóp tam giác, do đó trong nhiều trường hợp ta cần hoạt phân chia hình chóp đã cho thành nhiều hình chóp tam giác khác nhau rồi mới áp dụng.

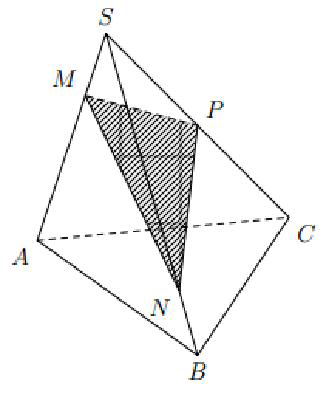
Một số trường hợp đặc biệt

Nếu (A₁B₁C₁D₁) // (ABCD) và thì

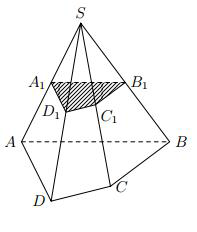
Kết quả vẫn đúng trong trường hợp đáy là n − giác.

6. Tỉ số thể tích của khối lăng trụ

Lăng trụ tam giác

Gọi V là thể tích khối lăng trụ, V₍₄₎ là thể tích khối chóp tạo thành từ 4 trong 6 đỉnh của lăng trụ,

V₍₅₎ là thể tích khối chóp tạo thành từ 5 trong 6 đỉnh của lăng trụ. Khi đó:

V₍₄₎ =

V₍₅₎ =

Ví dụ:

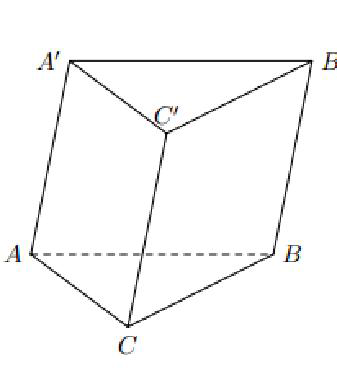
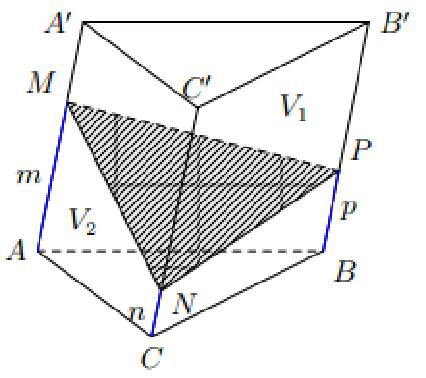
Mặt phẳng cắt các cạnh bên của lăng trụ tam giác

Gọi V₁, V₂ và V lần lượt là thể tích phần trên, phần dưới và lăng trụ. Giả sử

Khi đó:

Khi M ≡ A’, N ≡ C thì

Khối hộp

7. Tỉ số thể tích của khối hộp

Gọi V là thể tích khối hộp, V₍₄₎ là thể tích khối chóp tạo thành từ 4 trong 8 đỉnh của khối hộp. Khi đó:

V₍₄₎ (hai đường chéo của hai mặt phẳng song song) =

V₍₄₎ (trường hợp còn lại) =

Ví dụ:

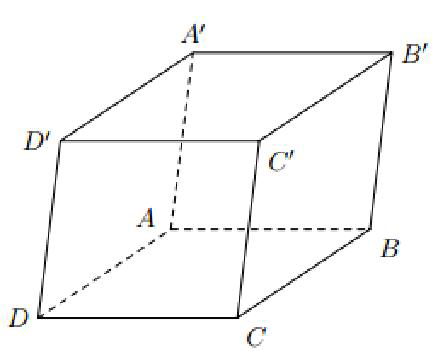
Mặt phẳng cắt các cạnh của hình hộp (chỉ quan tâm tới hai cạnh đối nhau)

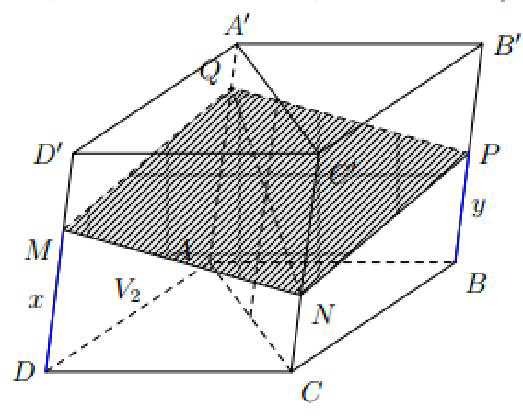
Theo từng bài toán khác nhau

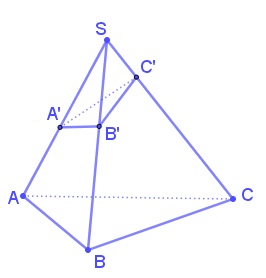
Bài toán 1: Tỉ số thể tích hình chóp tam giác

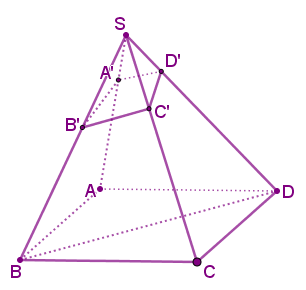
Bài toán 2: Tỉ số thể tích hình chóp tứ giác có đáy là hình bình hành.

Đặt

Khi đó:

+) a + c = b + d.

+)

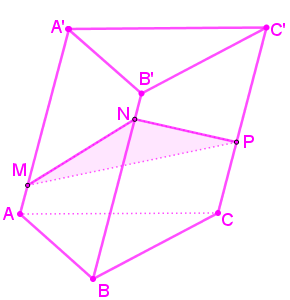
Bài toán 3: Tỉ số thể tích hình chóp lăng trụ tam giác.

Giả sử

Khi đó:

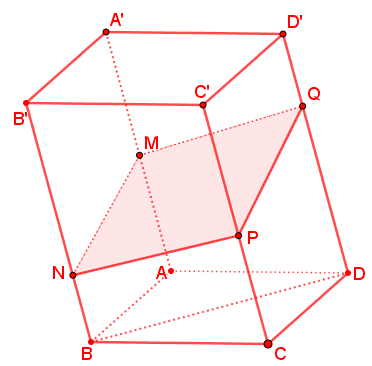
Bài toán 4: Tỉ số thể tích hình hộp

Giả sử

Khi đó

+) x + y = z + t.

+)

Kiến thức khác: Tỉ số thể tích hình chóp chung đỉnh hoặc chung đáy.

Hai hình chóp có chung đáy thì

Hai hình chóp có chung đỉnh và hai đáy nằm trên một mặt phẳng thì

Dạng 1: Tỉ số thể tích khối chóp tam giác

Câu 1: Cho hình chóp S.ABC. Gọi M, N, P lần lượt là trung điểm của SA, SB, SC. Tỉ số thể tích bằng

A. 12

B. 2

C. 8

D. 3

Lời giải

Chọn C

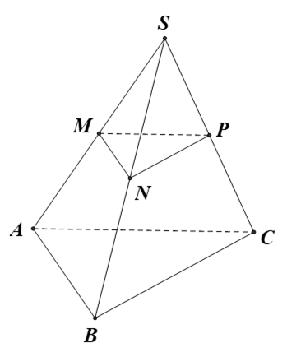
Ta có:

Câu 2: Cho tứ diện MNPQ. Gọi I; J; K lần lượt là trung điểm của các cạnh MN; MP; MQ. Tỉ số thể tích bằng

A.

B.

C.

D.

Lời giải

Chọn D

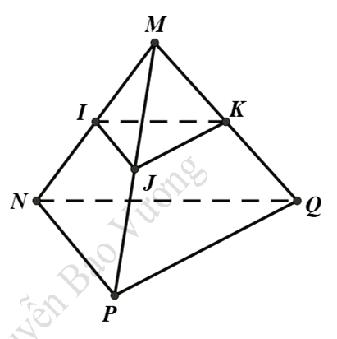
Ta có:

Câu 3: Cho hình chóp S.ABCD. Gọi A’, B’, C’, D’ theo thứ tự là trung điểm của SA, SB, SC, SD. Tính tỉ số thể tích của hai khối chóp S.A’B’C’D’ và S.ABCD .

A.

B.

C.

D.

Lời giải

Chọn C

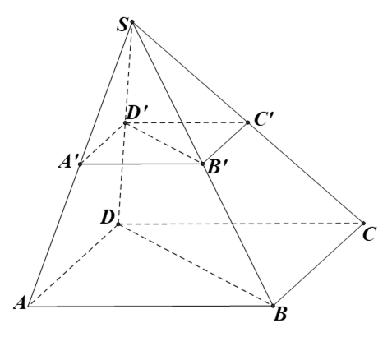
Ta có:

Và

Suy ra

Câu 4: Cho hình chóp S.ABC. Gọi M, N, P theo thứ tự là trung điểm của SA, SB, SC. Tính tỉ số thể tích của 2 khối chóp S.MNP và S.ABC bằng

A.

B.

C.

D.

Lời giải

Chọn B

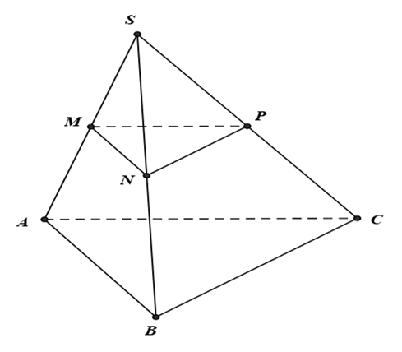
Ta có

Câu 5: Cho khối chóp S.ABC có thể tích V. Gọi B’, C’ lần lượt là trung điểm của AB, AC. Tính theo V thể tích khối chóp S.AB’C’

A.

B.

C.

D.

Lời giải

Chọn D

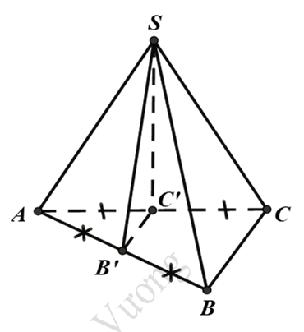
Ta có tỷ số thể tích .

Do đó hay

Câu 6: Cho hình chóp S.ABCD, gọi I, J, K, H lần lượt là trung điểm các cạnh SA, SB, SC, SD. Tính thể tích khối chóp S.ABCD biết thể tích khối chóp S.IJKH bằng 1.

A. 16

B. 8

C. 2

D. 4

Lời giải

Chọn B

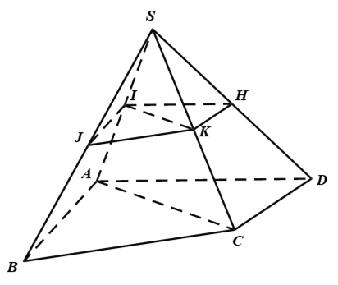
Ta có:

Do đó: V_S.ABCD = 8V_S.IJKH = 8.

Câu 7: Cho hình chóp S.ABC, trên các tia SA, SB, SC lần lượt lấy các điểm A ‘, B ‘, C ‘. Gọi V₁, V₂ lần lượt là thể tích khối chóp S.ABC và S.A’B’C’. Khẳng định nào sau đây là đúng?

A.

B.

C.

D.

Lời giải

Chọn D

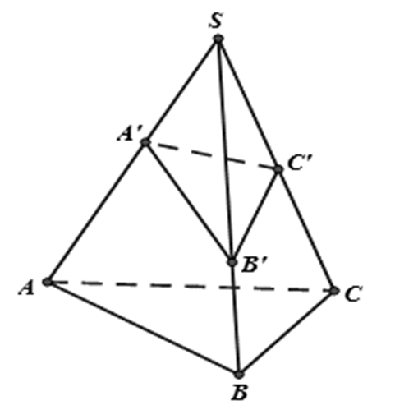
Theo công thức tỉ số thể tích ta có

Câu 8: Cho khối chóp SABC có thể tích bằng 5a³. Trên các cạnh SB, SC lần lượt lấy các điểm M và N sao cho SM = 3MB, SN = 4NC (tham khảo hình vẽ). Tính thể tích V của khối chóp AMNCB.

A.

B.

C. V = a³

D. V = 2a³

Lời giải

Chọn D

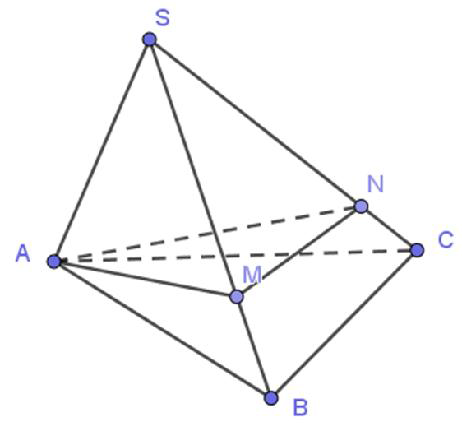
Gọi V₁ là thể tích khối chóp S.AMN và V₀ là thể tích khối chóp S.ABC.

Theo công thức tỷ lệ thể tích ta có:

V là thể tích khối chóp AMNCB ta có V + V₁ = V₀.

Vậy

Câu 9:  Nếu một hình chóp tứ giác đều có chiều cao và cạnh đáy cùng tăng lên 2 lần thì thể tích của nó tăng lên bao nhiêu lần?

A. 2 lần

B. 4 lần

C. 6 lần

D. 8 lần

Lời giải

Chọn D

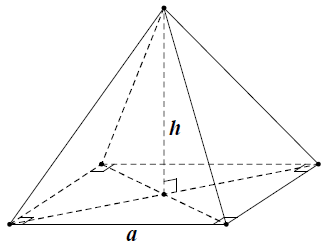
Gọi h, a lần lượt là chiều cao và cạnh đáy của hình chóp tứ giác đều.

Thể tích của khối chóp tứ giác đều là

Khi tăng chiều cao và cạnh đáy lên 2 lần thì ta được khối chóp tứ giác đều mới có thể tích là

Vậy thể tích của khối chóp tăng lên 8 lần.

Bài tập nâng cao

Câu 1: Cho tứ diện ABCD có thể tích V với M, N lần lượt là trung điểm AB, CD. Gọi V₁, V₂ lần lượt là thể tích của MNBC và MNDA. Tính tỉ lệ .

A. 1

B.

C.

D.

Lời giải

Chọn B

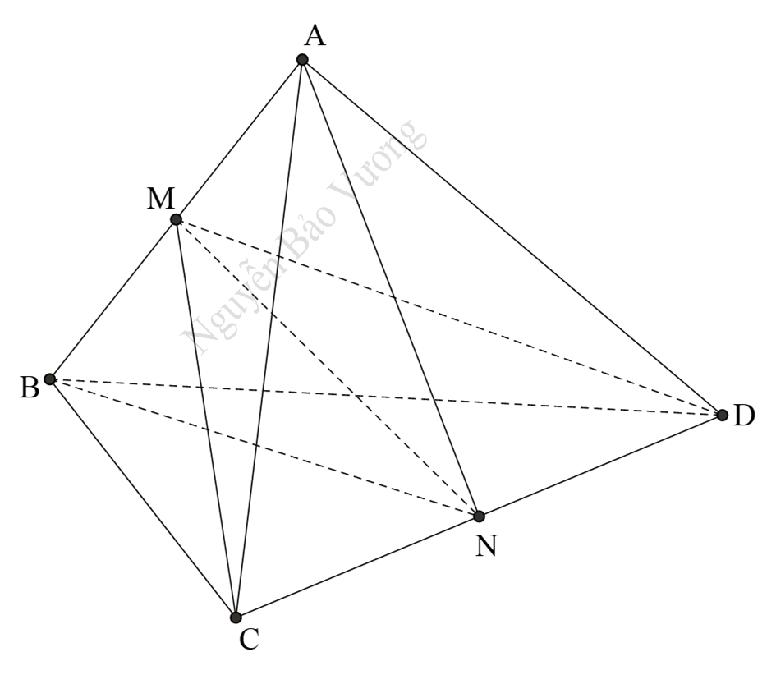
Vì M, N lần lượt là trung điểm AB, CD nên ta có:

d(A, (MCD)) = d(B, (MCD)); d(C, (NAB)) = d(D, (NAB)), do đó:

Câu 2: Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M và N là trung điểm các cạnh SA, SC, mặt phẳng (BMN) cắt cạnh SD tại P. Tỉ số bằng:

A.

B.

C.

D.

Lời giải

Chọn B

Dựng SO ∩ MN = {I}, SI ∩ SD = {P} , OE // BP;

Khi đó: I là trung điểm của MN, SO nên

Vậy

Câu 3: Cho tứ diện ABCD. Gọi B’, C’ lần lượt là trung điểm của AB và CD. Khi đó tỷ số thể tích của khối đa diện AB’C’D và khối tứ diện ABCD bằng

A.

B.

C.

D.

Lời giải

Chọn B

Ta có:

Câu 4: Cho hình chóp S.ABCD đáy là hình bình hành. Gọi M, N lần lượt là trung điểm của SA, SC. Mặt phẳng (BMN) cắt SD tại P. Tỉ số bằng:

A.

B.

C.

D.

Lời giải

Chọn B

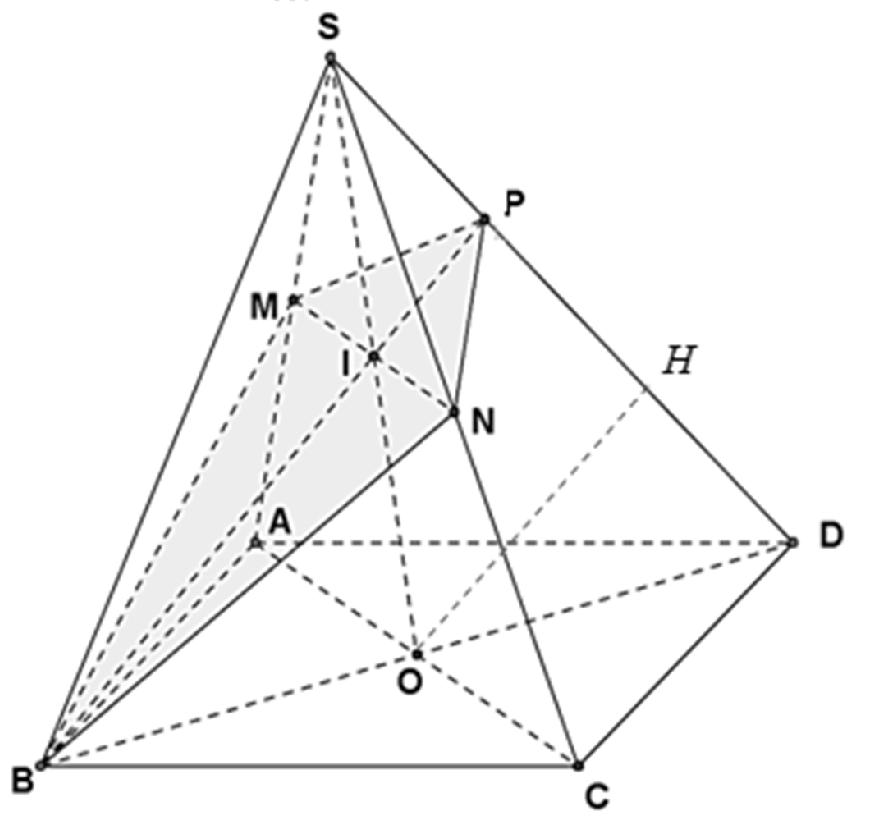
Ta có M, N là trung điểm của SA, SC nên

Cách 1: Áp dụng định lý Menelaus cho ∆SOD ta có:

Cách 2: Kẻ OH // BP, ta có O là trung điểm của BD nên H là trung điểm của PD. Ta có OH // IP mà I là trung điểm của SO nên P là trung điểm của SH.

Suy ra:

Theo công thức tỉ số thể tích ta có:

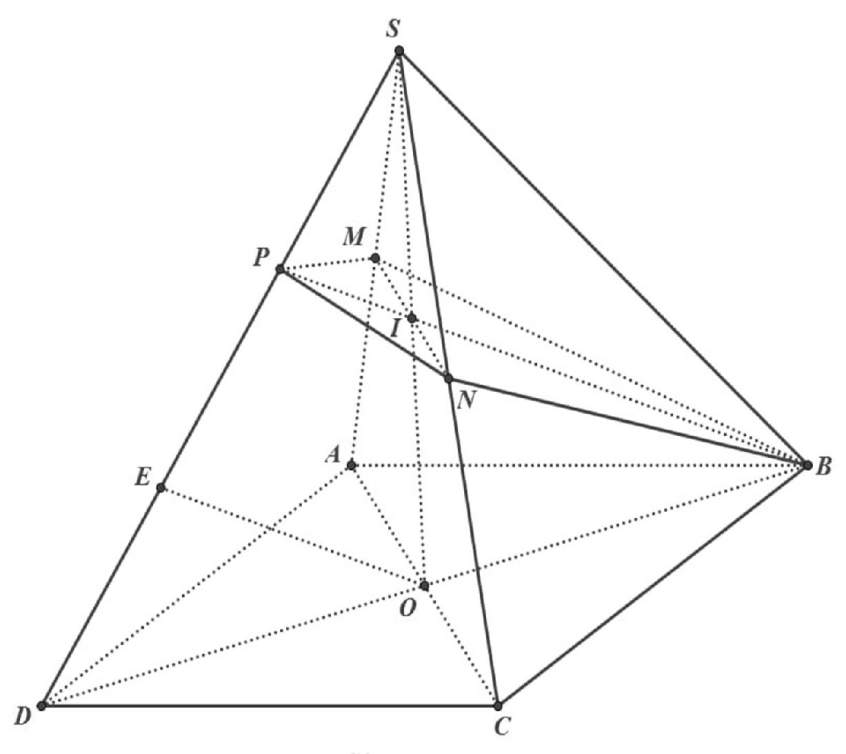
Câu 5: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi K, M lần lượt là trung điểm của các đoạn thẳng SA, SB, (α) là mặt phẳng qua K song song với AC và AM. Mặt phẳng (α) chia khối chóp S.ABCD thành hai khối đa diện. Gọi V₁ là thể tích của khối đa diện chứa đỉnh S và V₂ là thể tích khối đa diện còn lại. Tính tỉ số

A.

B.

C.

D.

Lời giải

Chọn D

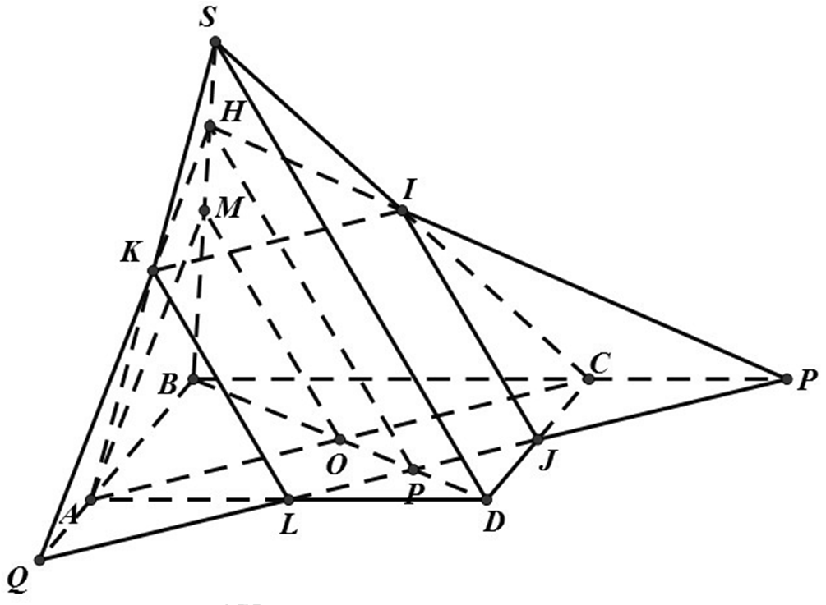
Gọi V là thể tích khối chóp S.ABCD; I, H lần lượt là trung điểm SC, SM. Do (α) // (ACM ) nên (α) cắt (SAD), (SBD), (SCD) lần lượt tại KL, HP, IJ cùng song song với OM .

Ta có . Suy ra

Tương tự:

Do đó

Vậy tỉ số

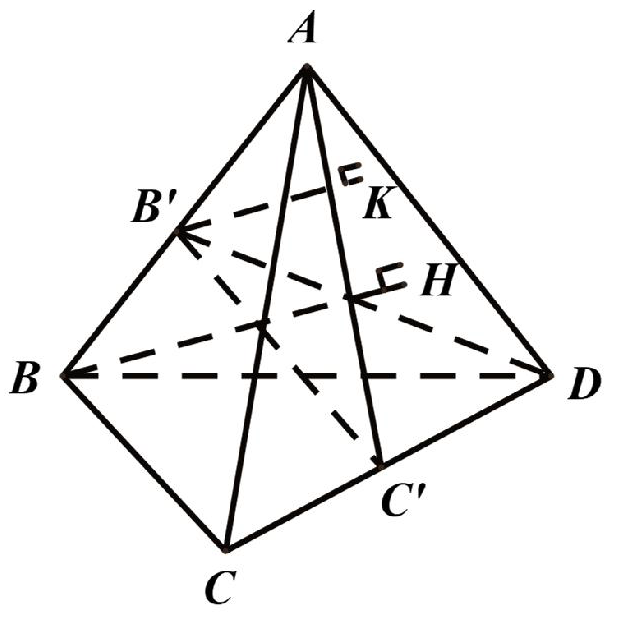
Câu 6: Cho hình chóp tứ giác đều S.ABCD. Mặt phẳng (P) qua A và vuông góc với SC cắt SB, SC, SD lần lượt tại B’, C’, D’. Biết C’ là trung điểm của SC. Gọi V₁, V₂ lần lượt là thể tích hai khối chóp S.AB’C’D’ và S.ABCD. Tính tỷ số

A.

B.

C.

D.

Lời giải

Chọn D

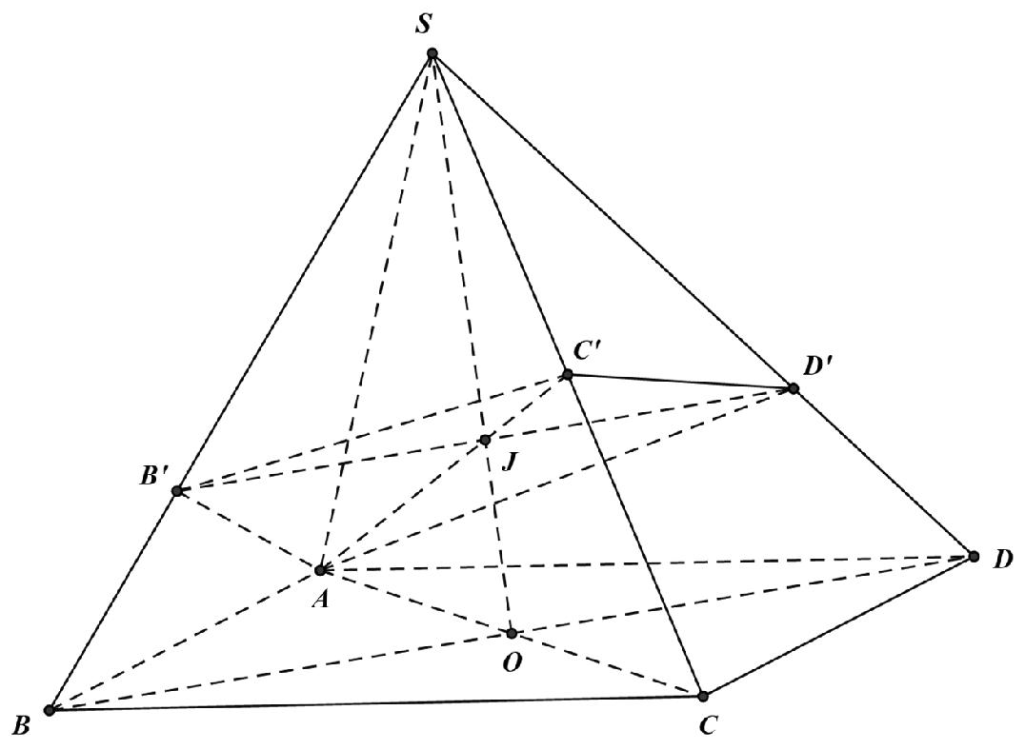
Ta có V₂ = 2․V_S.ABC = 2․V_S.ACD. Gọi O = AC ∩ BD, J = SO ∩ AC’.

Vì C’ là trung điểm của SC nên J là trọng tâm của ∆SAC.

Vì BD ⊥ (SAC) ⇒ BD ⊥ SC mà (P) qua A và vuông góc với SC nên (P) // BD.

Trong (SBD) qua J kẻ đường thẳng song song với BD cắt SB, SD lần lượt tại B’, D’.

Ta có

Khi đó

Câu 7: Cho hình chóp S.ABCD. Gọi A’, B’, C’, D’ theo thứ tự là trung điểm của SA, SB, SC, SD. Tính tỉ số thể tích của hai khối chóp S.A’B’C’D’ và S.ABCD.

A.

B.

C.

D.

Lời giải

Chọn C

Ta có:

Mà V_S.ABCD = V_S.ABC + V_S.ACD, suy ra

Dạng 2: Tỉ số khối lăng trụ

Câu 1: Cho khối lăng trụ ABC.A’B’C’ có thể tích bằng V. Tính thể tích khối đa diện BAA’C’C.

A.

B.

C.

D.

Lời giải

Chọn B

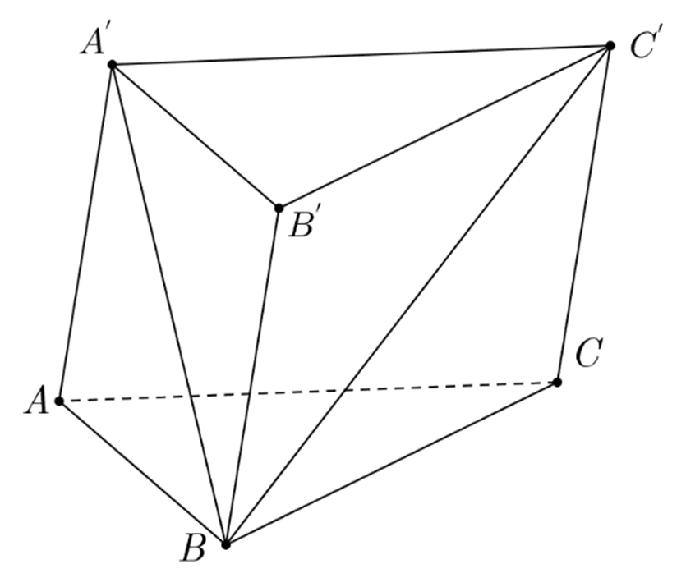
Mặt phẳng (BA’C’) chia khối lăng trụ ABC.A’B’C’ thành hai khối: B.AA’C’C và B.A’B’C’

⇒ V_B.AA’C’C = V_{ABC.A’B’C’} − V_{B.A’B’C’.}

Khối chóp B.A’B’C’ và khối lăng trụ có chung đáy và chung chiều cao

Câu 2: Cho lăng trụ ABC.A’B’C’, M là trung điểm CC’. Mặt phẳng (ABM) chia khối lăng trụ thành hai khối đa diện. Gọi V₁ là thể tích khối lăng trụ chứa đỉnh C và V₂ là thể tích khối đa diện còn lại. Tính tỉ số

A.

B.

C.

D.

Lời giải

Chọn A

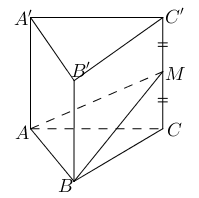
V₁ là thể tích khối lăng trụ chứa đỉnh C tức là

V₂ là thể tích khối đa diện còn lại

Khi đó ta có tỉ số

Câu 3: Khối lăng trụ ABC.A’B’C’ có thể tích bằng 6. Mặt phẳng (A’BC’) chia khối lăng trụ thành một khối chóp tam giác và một khối chóp tứ giác có thể tích lần lượt là

A. 2 và 4

B. 3 và 3

C. 4 và 2

D. 1 và 5

Lời giải

Chọn A

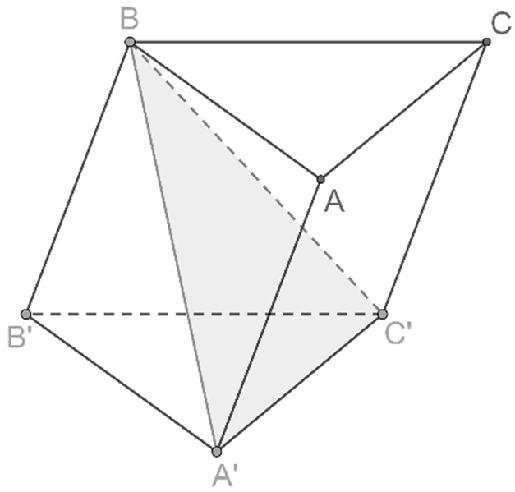
Thể tích khối lăng trụ là: V_{ABC.A’B’C’} = d (B, (A’B’C’))․S_A’B’C’ = 6.

Thể tích khối chóp tam giác B.A’B’C’ là:

Vậy thể tích khối chóp tứ giác B.ACC’A’ là: V_B.ACC’A’ = V_{ABC. A’B’C’} − V_{B. A’B’C’} = 6 – 2 = 4.

Câu 4: Cho khối lăng trụ tam giác ABC.A’B’C’ có thể tích V. Gọi M là trung điểm của cạnh CC’. Mặt phẳng (MAB) chia khối lăng trụ thành hai phần có tỉ số k ≤ 1 . Tìm k?

A.

B.

C.

D.

Lời giải

Chọn C

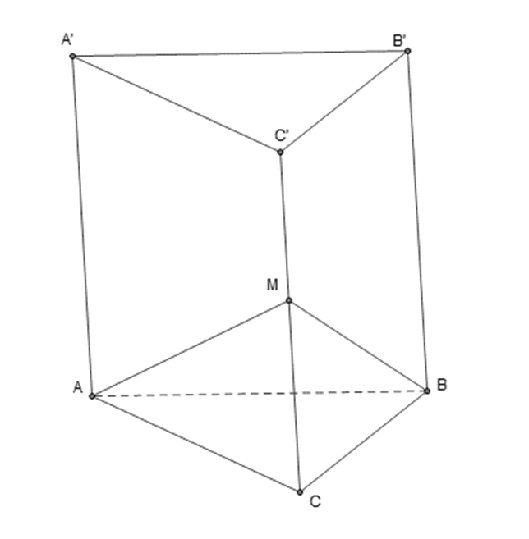
Ta có V = d(C’, (ABC))․S_ABC

Khi đó

Vậy

Câu 5: Một khối lăng trụ tứ giác đều có thể tích là 4. Nếu gấp đôi các cạnh đáy đồng thời giảm chiều cao của khối lăng trụ này hai lần thì được khối lăng trụ mới có thể tích là:

A. 8

B. 4

C. 16

D. 2

Lời giải

Chọn A

Giả sử khối lăng trụ tứ giác đều có độ dài cạnh đáy là a và chiều cao là h. Khi đó thể tích khối lăng trụ tứ giác đều được tính bởi công thức V = B․h = a²․h = 4.

Nếu gấp đôi các cạnh đáy thì diện tích đáy mới B’ = 4a². Giảm chiều cao hai lần nên chiều cao mới . Vì vậy thể tích khối lăng trụ mới sẽ là:

Câu 6:  Biết khối hộp ABCD.A’B’C’D’ có thể tích V. Nếu tăng mỗi cạnh của hình hộp đó lên gấp hai lần thì thể tích khối hộp mới là:

A. 8V

B. 4V

C. 2V

D. 16V

Lời giải

Chọn A

Ta có nếu tăng mỗi cạnh của khối hộp lên hai lần thì ta được khối hộp mới đồng dạng với khối hộp cũ theo tỉ số 2. Do đó thể tích khối hộp mới bằng 2³․V = 8V

Câu 7: Cho hình lăng trụ đứng ABC.A’B’C’ có M là trung điểm của AA’. Tỉ số thể tích bằng

A.

B.

C.

D.

Lời giải

Chọn A

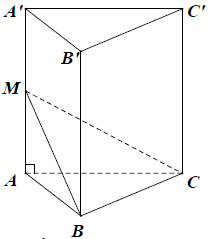
Ta có:

Câu 8: Cho lăng trụ tam giác ABC.A’B’C’ có thể tích là V. Gọi M là trung điểm cạnh AA’. Khi đó thể tích khối chóp M.BCC’B’ là

A.

B.

C.

D.

Lời giải

Chọn B

Vì AA’// (BB’C’C) nên d(M, (BB’C’C)) = d(A, (BB’C’C)) suy ra V_M.BB’C’C = V_A.BB’C’C

Mà

Vậy

Câu 9: Cho lăng trụ ABC.A’B’C’. Biết diện tích mặt bên (ABB’A’) bằng 15, khoảng cách từ điểm C đến (ABB’A’) bằng 6. Tính thể tích khối lăng trụ ABC.A’B’C’.

A. 30

B. 45

C. 60

D. 90

Lời giải

Chọn B

Ta có

Mà

Câu 10: Cho khối lăng trụ ABC.A’B’C’ có thể tích bằngV. Tính thể tích khối đa diện ABCB’C’.

A.

B.

C.

D.

Lời giải

Chọn D

Gọi chiều cao của lăng trụ là h, S_ABC = S_A’B’C’ = S. Khi đó V = S․h.

Ta có

Câu 11: Cho hình hộp ABCD.A’B’C ‘D’ có I là giao điểm của AC và BD. Gọi V₁ và V₂ lần lượt là thể tích của các khối ABCD.A’B’C’D’ và I.A’B’C’. Tính tỉ số

A.

B.

C.

D.

Lời giải

Chọn A

Ta có: V₁ = AA’․S_{A’B’C’D ‘}

Dạng 3: Ứng dụng tỉ số thể tích để tính thể tích

Câu 1: Cho tứ diện ABCD có các cạnh AB, AC và AD đôi một vuông góc với nhau; AB = 6a, AC = 7a và AD = 4a. Gọi M, N, P tương ứng là trung điểm các cạnh BC, CD, DB. Tính thể tích V của tứ diện AMNP.

A.

B.

C.

D.

Lời giải

Chọn D

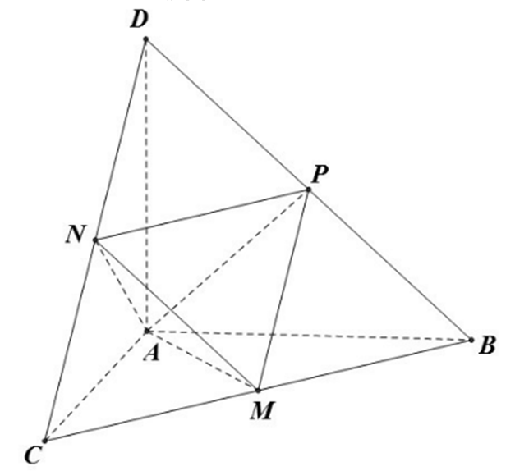
Ta có

Ta nhận thấy

Câu 2: Cho hình chóp S.ABCD, gọi I, J, K, H lần lượt là trung điểm các cạnh SA, SB, SC, SD. Tính thể tích khối chóp S.ABCD biết thể tích khối chóp S.IJKH bằng 1.

A. 16

B. 8

C. 2

D. 4

Lời giải

Chọn B

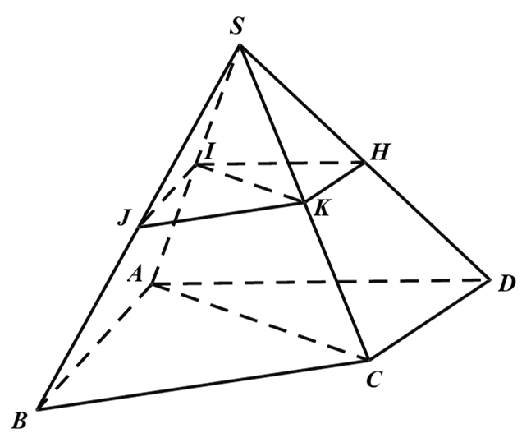
Ta có:

Do đó: V_S.ABCD = 8V_S.IJKH = 8.

Câu 3: Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh 2a. Mặt bên tạo với đáy góc 60^°. Gọi K là hình chiếu vuông góc của O trên SD. Tính theo a thể tích khối tứ diện DKAC.

A.

B.

C.

D.

Lời giải

Chọn A

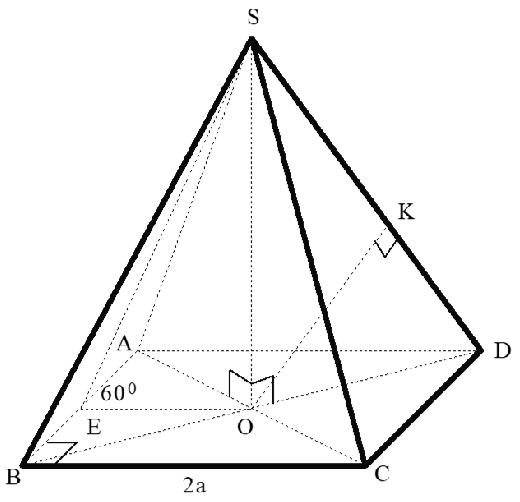
Gọi E là trung điểm của AB, O là tâm của hình vuông ABCD.

⇒ OE ⊥ AB, SO ⊥ AB

⇒ AB ⊥ (SOE).

⇒ Góc giữa mặt bên (SAB) và mặt đáy (ABCD) là

∆SOD có đường cao OK

Vậy

Câu 4: Cho khối chóp S.ABCD có thể tích bằng 32. Gọi M, N, P, Q lần lượt là trung điểm SA, SB, SC, SD. Thể tích khối chóp S.MNPQ bằng

A. 16

B. 8

C. 4

D. 2

Lời giải

Chọn C

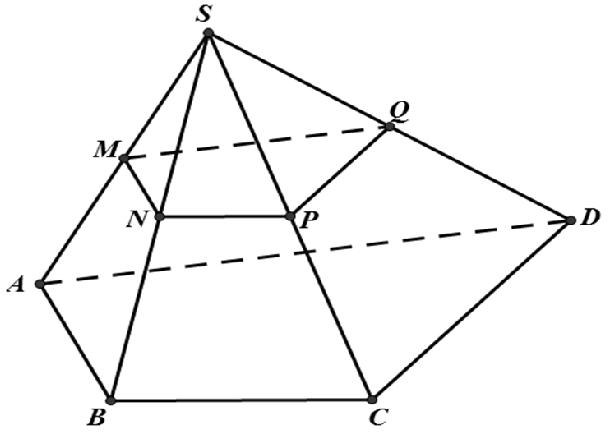
Ta có

Do đó

Vậy V_S.MNPQ = 4.

Câu 5: Cho hình chóp S.ABCD có đáy ABCD là hình thoi. Gọi D’ là trung điểm SD, mặt phẳng chứa BD’ và song song với AC lần lượt cắt các cạnh SA, SC tại A’ và C’. Biết thể tích khối chóp

S.A’BC’D’ bằng 1, tính thể tích V của khối chóp S.ABCD.

A.

B.

C.

D.

Lời giải

Chọn D

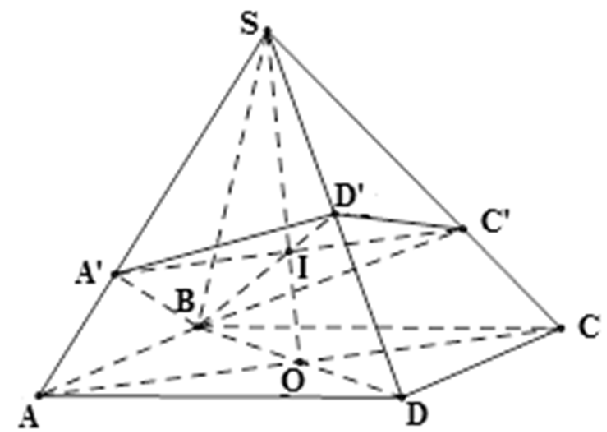
Gọi O là tâm hình bình hành đáy và {I} = SO ∩ BD’.

Mặt phẳng được nói đến đi qua I và song song AC nên cắt (SAC) theo giao tuyến là đường thẳng A’C’ qua I và song song AC (với A’ ∈ SA, C’ ∈ SC).

I là trọng tâm tam giác SBD nên

Ta có:

Câu 6:  Cho tứ diện ABCD có thể tích bằng 1. Gọi M, N, P lần lượt là trọng tâm của tam giác ABC, ACD, ABD. Tính thể tích của tứ diện AMNP.

A.

B.

C.

D.

Lời giải

Chọn D

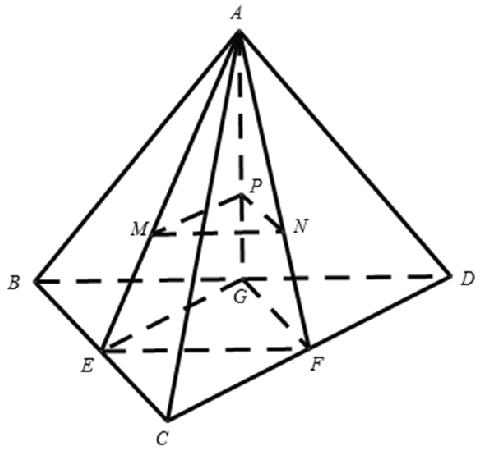
Gọi E, F, G lần lượt là trung điểm của BC, CD và DB

Ta có

Câu 7: Cho khối chóp S.ABCD có thể tích bằng 18, đáy ABCD là hình bình hành. Điểm M thuộc cạnh SD sao cho SM = 2MD. Mặt phẳng (ABM) cắt đường thẳng SC tại N. Thể tích khối chóp S.ABNM bằng

A 6

B 10

C 12

D 8

Lời giải

Chọn B

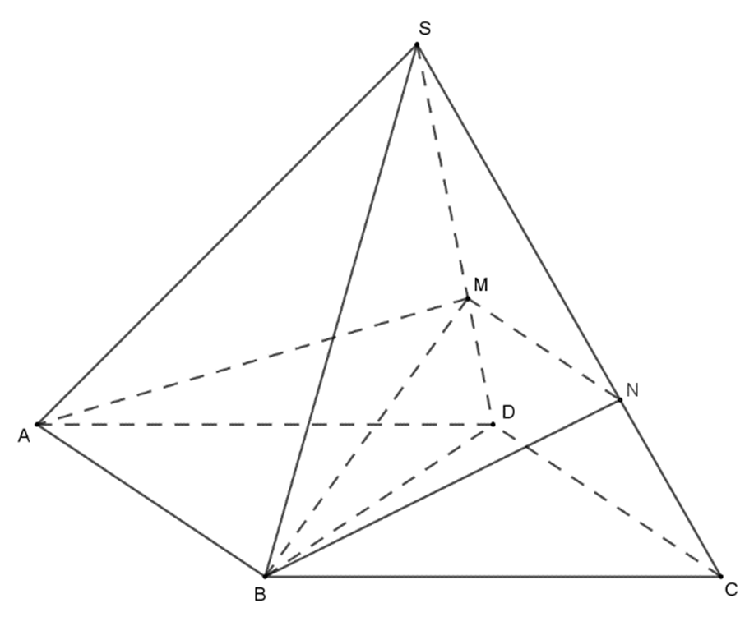
Mặt phẳng (MAB) và mặt phẳng (SCD) có chung điểm M và lần lượt chứa hai đường thẳng song song AB và CD nên MN // AB // CD.

Vì ABCD là hình bình hành nên

Ta có:

Chú ý: Có thể áp dụng công thức tỉ số thế tích và tính như sau:

Ta có: