Bạn đang xem bài viết Tổng quan lý thuyết và một số dạng bài tập phổ biến. Hi vọng sẽ là đáp án bạn ưng ý. Cùng theo dõi nhé!
Bài viết giúp các bạn học sinh nắm vững lý thuyết số phức, 8 dạng bài tập phổ biến và một số tài liệu hay nhất cho chuyên đề này. Phần lý thuyết được đánh giá là không quá khó, do đó bạn có thể đi nhanh nhưng cần nắm vững một số khái niệm cốt lõi như: phần thực, phần ảo, các phép cộng trừ nhân chia giữa hai hay nhiều số phức.
Tổng quan số phức
Số phức được sử dụng nhiều trong khoa học, kỹ thuật, điện cơ, cơ học lượng tử,… Tuy nhiên bài viết sau đây, chúng ta sẽ gói gọn tìm hiểu lý thuyết cơ bản được hiểu theo toán học chương trình 12 và một số dạng toán xuất hiện trong các kì thi quan trọng.
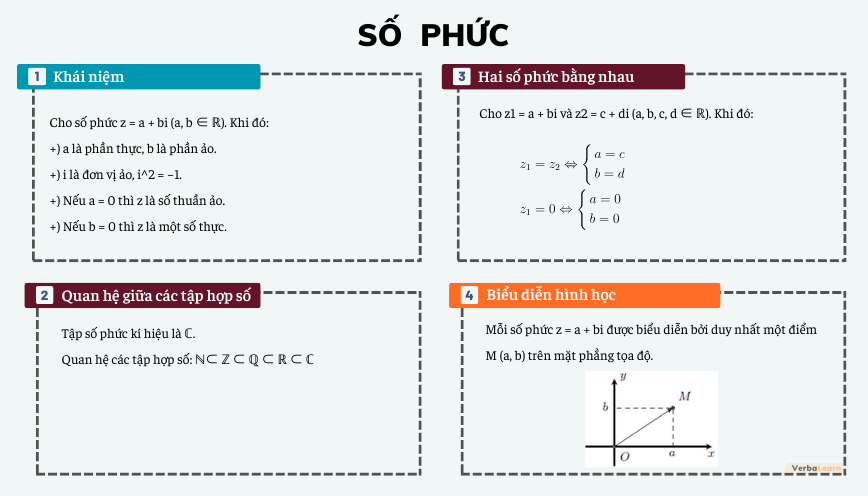
1. Khái niệm
Cho số phức z = a + bi (a, b ∈ ℝ). Khi đó:
+) a là phần thực, b là phần ảo.
+) i là đơn vị ảo, i2 = −1.
+) Nếu a = 0 thì z là số thuần ảo.
+) Nếu b = 0 thì z là một số thực.
2. Quan hệ giữa các tập hợp số
Tập số phức kí hiệu là ℂ.
Quan hệ các tập hợp số: ℕ⊂ ℤ ⊂ ℚ ⊂ ℝ ⊂ ℂ
3. Hai số phức bằng nhau
Cho z1 = a + bi và z2 = c + di (a, b, c, d ∈ ℝ). Khi đó:
4. Biểu diễn hình học của số phức
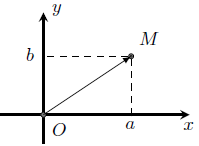Biểu diễn hình học của số phức
Mỗi số phức z = a + bi được biểu diễn bởi duy nhất một điểm
M (a, b) trên mặt phẳng tọa độ.
5. Mô-đun số phức
5.1. Khái niệm Mô-đun số phức
Độ dài của véc–tơ 
được gọi là mô-đun của số phức z và kí hiệu là |z|.
Từ định nghĩa, suy ra 
hay 
5.2. Tính chất
+) |z| ≥ 0, ∀z ∈ ℂ; |z| = 0 ⇔ z = 0.
+) |z.z’| = |z|. |z’|.
+) 
+) ||z| − |z’|| ≤ |z ± z’| ≤ |z| + |z’|.
6. Số phức liên hợp
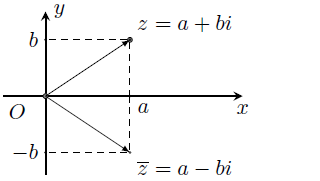Số phức liên hợp
Cho số phức z = a + bi (a, b ∈ ℝ).
Ta gọi a − bi là số phức liên hợp của z và kí hiệu là 
.
Vậy 
hay 
Chú ý: 
7. Phép toán trên số phức
7.1. Cộng, trừ hai số phức
Ta cộng (trừ) phần thực theo phần thực, phần ảo theo phần ảo.
(a + bi) + (c + di) = (a + c) + (b + d) i.
(a + bi) −(c + di) = (a − c) + (b − d) i.
7.2. Phép nhân hai số phức
Ta nhân phân phối, tương tự nhân hai đa thức. Lưu ý: i2 = −1.
(a + bi)(c + di) = (ac − bd) + (ad + bc) i
7.3. Phép chia hai số phức
Cho hai số phức z1 = a + bi và z2 = c + di. Thực hiện phép chia 
, ta nhân thêm 
ở tử và mẫu.
Số phức nghịch đảo của z là 
Lũy thừa của đơn vị ảo:
i2 = −1.
i3 = −i
in = 1 nếu n chia hết cho 4.
in = i nếu n chia 4 dư 1
in = −1 nếu n chia 4 dư 2
in = −i nếu n chia 4 dư 3
8. Phương trình bậc hai với hệ số thực
Xét phương trình ax2 + bx + c = 0, với a, b, c ∈ ℝ và a ≠ 0. Đặt ∆ = b2 – 4ac, khi đó:
Nếu ∆ ≥ 0 thì phương trình có nghiệm 
Nếu ∆ < 0 thì phương trình có nghiệm 
Định lý Viet: 
và 
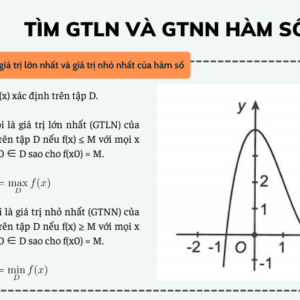
Các dạng bài tập số phức
Dạng 1. Xác định các đại lượng liên quan đến số phức
Phương pháp giải
Biến đổi số phức z về dạng A + Bi
Khi đó:
+) Phần thực là A
+) Phần ảo là B
+) Số phức liên hợp là 
+) Mô-đun bằng 
Bài tập vận dụng
Câu 1. Xác định phần thực và phần ảo của số phức z, biết:
a) z = (2 + 3i) + (5 – 3i)
b) z = (3 + 2i)2
c) 
Hướng dẫn giải
a) z = (2 + 3i) + (5 – 3i) = (2 + 5) + (3 – 3)i =7. Phần thực là 7, phần ảo là 0.
b) z = (3+ 2i)2 = 9 + 12i + 4i2 = 9 + 12i – 4 = 5 + 12i. Phần thực là 5, phần ảo là 12.
c) 
. Phần thực là 5, phần ảo là –2.
Câu 2. Tìm nghịch đảo của số phức z = 2 – 3i.
Hướng dẫn giải
Nghịch đảo của z là 
.
Ta có 
Câu 3. Tìm phần thực và phần ảo của số phức 
Hướng dẫn giải
Vậy số phức z có phần thực bằng 2 và phần ảo bằng 2.
Câu 4. Cho z1 = 3 + i và z2 = 2 – 3i. Tính:
a) |z1|
b) |z2|
c) |z1 + z1z2|
Hướng dẫn giải
a) 
b) 
c) z1 +z1z2 = 3 + i + (3 + i) (2 – 3i) = 10 = 12 – 6i. Suy ra 
Câu 5. Tính mô-đun của số phức sau:
a) 
b) 
c) 
Hướng dẫn giải
a) Áp dụng tính chất mô-đun của một tích, ta được: 
b) Áp dụng tính chất mô-đun của một thương, ta được: 
c) Áp dụng tính chất mô-đun của một thương, ta được: 
Câu 6. Cho Số phức z thỏa 
. Tính mô-đun của số phức ω = (3 + i)z.
Hướng dẫn giải
ω = (3 + i)z ⇒ |ω| = |(3 + i)z| = |3+ i| . |z| = 
Vậy |ω| = 
Câu 7. Cho Số phức z = m + (3m + 2)i , m là số thực âm, thỏa mãn |z| = 2. Tìm phần ảo của z.
Hướng dẫn giải
Vì m là số thực âm nên chọn 
, suy ra 
Dạng 2. Số phức bằng nhau
Phương pháp giải
Bài tập vận dụng
Câu 1. Tìm các số thực x,y thỏa mãn 3x + 2yi = 3y + 2 + (1 − x)i . Tìm x, y.
Hướng dẫn giải
Điều kiện đã cho tương đương với 
Câu 2. Cho số phức z = m2 – 4 + (m − 2)i. Tìm tất cả các giá trị thực của tham số m để z = 0.
Hướng dẫn giải
Điều kiện đã cho tương đương với: 
Dạng 3. Điểm biểu diễn số phức
Phương pháp giải
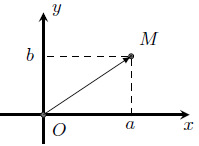
Mỗi số phức z = a + bị được biểu diễn bởi duy nhất một điểm
M(a, b) trên mặt phẳng tọa độ.
Bài tập vận dụng
Câu 1. Gọi M là điểm biểu diễn số phức z = i(1 + 2i)2. Tìm tọa độ của điểm M.
Hướng dẫn giải
Ta có z = i(1 + 2i)2 = i(1+ 4i + 4i2) = i(−3 + 4i) = – 4 – 3i ⇒ M (−4; −3).
Câu 2. Cho số phức z =1– 2i. Tìm tọa độ điểm biểu diễn của Số phức ω = iz.
Hướng dẫn giải
ω = iz = i(1 – 2i) = 2 + i. Suy ra, điểm biểu diễn có tọa độ là (2; 1)
Câu 3. Biểu diễn trên mặt phẳng tọa độ các số phức sau: 4 − 3i, 3 + 2i, −5, 5i.
Hướng dẫn giải
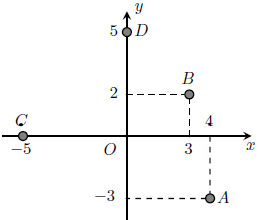
Điểm A(4; −3) biểu diễn số phức 4 – 3i.
Điểm B(3; 2) biểu diễn số phức 3 + 2i.
Điểm C(−5; 0) biểu diễn số phức –5
Điểm D(0; 5) biểu diễn số phức 5i
Câu 4. Trong mặt phẳng tọa độ Oxy, gọi M là điểm biểu diễn số phức z = 3 – 4i, N là điểm biểu diễn cho số phức 
. Tính diện tích của tam giác OMN.
Hướng dẫn giải
Ta có M (3; −4) và 
Dễ thấy tam giác OMN vuông tại N nên 
Câu 5. Cho số phức z thỏa mãn 
và điểm A trong hình vẽ bên là điểm biểu diễn của z. Tìm điểm biểu diễn số phức 
trong hình vẽ bên, biết đó là một trong bốn điểm M, N, P, Q.
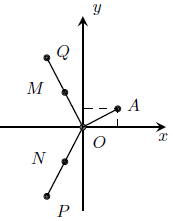
Hướng dẫn giải
Do điểm A là điểm biểu diễn của z nằm trong góc phần tư thứ nhất của mặt phẳng Oxy nên gọi z = a + bi, với a, b > 0.
Ta có: 
. Do ω có phần thực và ảo đều âm nên điểm biểu diễn ω chỉ có thể là điểm P hoặc N.
Mặt khác: 
, nên điểm biểu diễn của số phức ω là điểm P.
Dạng 4. Lũy thừa với đơn vị ảo
Phương pháp giải
Các công thức biến đổi:
+) i2 = −1.
+) i3 = −i.
+) in = 1 nếu n chia hết cho 4.
+) in = i nếu n chia 4 dư 1.
+) in = −1 nếu n chia 4 dư 2
+) in = −i nếu n chia 4 dư 3
Tổng n số hạng đầu của một cấp số cộng:
hoặc 
, với u1 là số hạng đầu, d là công sai.
Tổng n số hạng đầu của một cấp số nhân:
, với u1 là số hạng đầu, q là công bội (q ≠ 1).
Bài tập vận dụng
Câu 1. Xác định số phức z, biết:
a) z = i2017+ i 2018 + i2019
b) z = (1 + i)15
Hướng dẫn giải
a) z = i2016․i + i2016․i2 + i2016․i3= i + i2 + i3 = –1
b) z = [(1 + i)2]7․(1 + i) = (2i)7․(1 + i) = 27․I7 (1 + i) = 27․(−i)․(1 + i) = 27 – 27․i
Câu 2. Tìm phần thực và phần ảo của số phức
Hướng dẫn giải
Vậy số phức z có phần thực bằng 0 và phần ảo bằng −1
Câu 3. Tìm mô-đun của số phức z = 1 + i + i2 + i3 + … + i100
Hướng dẫn giải
z được biểu diễn qua tổng của một cấp số nhân gồm 101 số hạng với u1 =1 và q= i.
Dạng 5. Phương trình với hệ số phức
Phương pháp giải
Trong chương trình, ta chỉ xét phương trình dạng này với ẩn z bậc nhất.
Ta giải tương tự như giải phương trình bậc nhất trên tập số thực;
Thực hiện các biến đổi đưa về dạng z = A + Bi
Bài tập vận dụng
Câu 1. Cho Số phức z thỏa mãn 
(1). Tìm môđun của số phức ω = z + 1 + i
Hướng dẫn giải
(1) ⇔ (2 + i)z + (3 + i) = 7 + 8i ⇔ (2 + i)z = (7 + 8i) – (3 + i) = 4 + 7i ⇔ 
Do đó: ω = (3 + 2i) + 1 + i = 4 + 3i. Suy ra: 
Câu 2. Tìm phần thực và phần ảo của số phức z thỏa (1 + i)2 (2 – i)z = 8 + i + (1 + 2i)z.
Hướng dẫn giải
(1 + i)2 (2 − i)․z = 8 + i + (1 + 2i)․z ⇔ 2i(2 – i)․z = 8 + i + (1 + 2i)․z
⇔ [2i(2 – i) – (1 + 2i)]․z = 8 + i ⇔ (1 + 2i)․z = 8 + i
⇔ 
Vậy số phức z có phần thực bằng 2 và phần ảo bằng –3.
Câu 3. Xác định số phức z thỏa 
Hướng dẫn giải
Dạng 6. Phương trình bậc hai với hệ số thực và một số phương trình quy về bậc hai
Phương pháp giải
Xét phương trình ax2 + bx + c = 0, với a, b, c ∈ ℝ và a ≠ 0. Đặt ∆ = b2 – 4ac, khi đó:
Nếu ∆ ≥ 0 thì phương trình có nghiệm 
Nếu ∆ < 0 thì phương trình có nghiệm 
Định lý Viet: 
và 
Bài tập vận dụng
Câu 1. Giải phương trình z2 – 3z + 10 = 0 trên tập số phức.
Hướng dẫn giải
∆ = (–3)2 – 4 × 1 × 10 = –31 = 31․i2;
Phương trình đã cho có hai nghiệm phức 
và 
Câu 2. Giải phương trình x2 + 4x + 5 = 0 trên tập số phức.
Hướng dẫn giải
∆’ = 22 – 1 × 5 = −1 = i2
Phương trình đã cho có hai nghiệm phức: x1 = −2 – i và x2 = −2 + i
Câu 3. Gọi z1 và z2 lần lượt là hai nghiệm của phương trình z2 – 2z + 5 = 0. Tính F = |z1| + |z2|.
Hướng dẫn giải
Giải phương trình z2 – 2z + 5 = 0 ta được hai nghiệm là z1 =1 + 2i và z2 = 1– 2i
Khi đó F = |z1| + |z2| = |1 + 2i| + |1 – 2i| = 
Câu 4. Giải phương trình z4 + 5z2 + 4 = 0 trên tập số phức.
Hướng dẫn giải
Đặt t = z2 thì phương trình thành t2 + 5t + 4 = 0 ⇔ 
Với t = −1 thì z2 = −1 ⇔ z = ±i
Với t = −4 thì z2 = −4 ⇔ z = ±2i
Vậy phương trình có bốn nghiệm là z = ±i và z = ±2i.
Dạng 7. Xác định số phức bằng cách giải hệ phương trình
Phương pháp giải
Gọi z = a + bi, Với a, b ∈ ℝ
+) Nếu đề bài cho dạng hai số phức bằng nhau, ta áp dụng một trong hai công thức sau:
+) Nếu đề bài cho phương trình ẩn z và kèm theo một trong các ẩn 
Ta thay z = a + bi vào điều kiện đề cho, đưa về “hai số phức bằng nhau”. Chú ý:
+) Nếu đề cho 2 thỏa hai điều kiện riêng biệt thì từ 2 điều kiện đó, ta tìm được hệ phương trình liên quan đến a, b. Giải tìm a, b.
Bài tập vận dụng
Câu 1. Tìm các số thực x, y biết (2x + 3y + 1) + (−x + 2y)․i = (3x −2y + 2) + (4x – y −3)․i.
Hướng dẫn giải
(2x + 3y + 1) + (−x + 2y)․i = (3x – 2y + 2) + (4x − y − 3)․i
Câu 2. Giải phương trình sau: 
(*)
Hướng dẫn giải
Giả sử z = a + bi với a, b ∈ ℝ. Khi đó:
(*) ⇔ a + bi + 2(a − bi) = 2 – 4i ⇔ 3a − bi = 2 – 4i ⇔ 
Vậy 
Câu 3. Cho Số phức z = a + bi, (a, b ∈ ℝ) thỏa mãn z + 1 + 3i – |z|i = 0. Tính S = a + 3b.
Hướng dẫn giải
Giả sử z = a + bi (a, b ∈ ℝ ). Thay vào z + 1 + 3i – |z|i =0 ta được
Suy ra: S = a + 3b = −5.
Câu 4. Tìm số phức z thỏa mãn: 
và z2 là số thuần ảo
Hướng dẫn giải
Giả sử z = a + bi (a, b ∈ ℝ), ta có:
và z2 = a2 – b2 + abi
Yêu cầu bài toán thỏa mãn khi và chỉ khi: 
Vậy các số phức cần tìm là: 1 + i; 1 – i; –1 + i; –1 – i
Câu 5. Xét số phức z thỏa mãn 
. Tính |z|
Hướng dẫn giải
Giả sử z = x + yi, với x, y ∈ ℝ. Ta có:
Suy ra z = 1 + i. Do đó:
Dạng 8. Biểu diễn hình học của số phức
Phương pháp giải
Trong mặt phẳng toạ độ Oxy, giả sử:
- M (x; y) là điểm biểu diễn của z = x + yi (x, y ∈ ℝ).
- N (x’; y’) là điểm biểu diễn của z’ = x’ + y’i (x’, y’ ∈ ℝ)
- I (a; b) là điểm biểu diễn của z0 = a + bi cho trước (a, b ∈ ℝ).
Khi đó, ta có các kết quả sau:
(khoảng cách từ điểm M đến gốc tọa độ O)
(khoảng cách giữa M và N)
|z – z0| ≤ R ⇔ (x − a)2 + (y – b)2 ≤ R2: hình tròn tâm I(a; b), bán kính R.
|z – z0| = R ⇔ (x − a)2 + (y – b)2 = R2: đường tròn tâm I(a; b), bán kính R.
Bài tập vận dụng
Câu 1. Trên mặt phẳng tọa độ, tìm tập hợp điểm biểu diễn các Số phức thỏa mãn điều kiện:
a) Phần thực của z bằng 3
b) Phần ảo của z bằng –5
Hướng dẫn giải
a) Số phức z có phần thực bằng 3 được biểu diễn bởi điểm M(3; b).
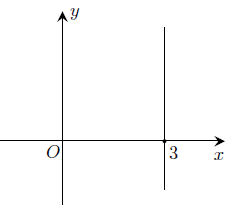
Vậy tập hợp các điểm biểu diễn số phức z là đường thẳng x = 3
b) Số phức z có phần ảo bằng −5 được biểu diễn bởi điểm M(a; −5).
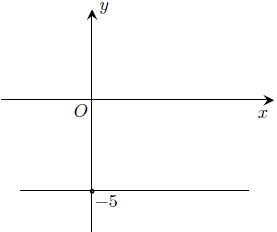
Vậy tập hợp các điểm biểu diễn số phức z là đường thẳng y = −5
Câu 2. Trên mặt phẳng tọa độ, tìm tập hợp điểm biểu diễn các số phức thỏa mãn:
a) Phần thực thuộc khoảng (–2; 3)
b) Phần ảo thuộc đoạn [–3; 3].
Hướng dẫn giải
a) Số phức z có phần thực thuộc khoảng (−2; 3) được biểu diễn bởi điểm M (a; b) với a ∈ −2; 3).
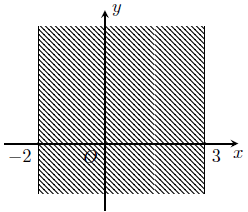
Vậy tập hợp các điểm biểu diễn số phức z là phần mặt phẳng giới hạn bởi hai đường thẳng x = −2 và x = 3
b) Số phức z có phần ảo thuộc khoảng [–3; 3] được biểu diễn bởi điểm M(a; b) với b ∈ [–3; 3]
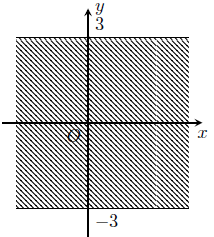
Vậy tập hợp các điểm biểu diễn số phức z là phần mặt phẳng giới hạn bởi hai đường thẳng y = −3 và y = 3, kể cả các điểm nằm trên hai đường thẳng này.
Câu 3. Tìm tập hợp điểm M thỏa: 
Hướng dẫn giải
Gọi M(x; y) là điểm biểu diễn số phức z = x + yi, với x, y ∈ ℝ
Vậy tập hợp điểm M là đường thẳng 
hoặc đường thẳng 
Câu 4. Tìm tập hợp điểm biểu diễn số phức z thỏa mãn |z – 1+ i| =1.
Hướng dẫn giải Gọi M (x, y) là điểm biểu diễn số phức z = x + yi, với x, y ∈ ℝ. Từ giả thiết ta có:
|z – 1 + i|=1 ⇔|(x −1) + (y + 1)i| = 1 ⇔ (x – 1)2 + (y + 1)2 = 1;
Vậy, tập hợp điểm M thuộc đường tròn tâm I(1; −1), bán kính bằng R = 1.
Câu 5. Cho các số phức z thỏa mãn |zi – (2 +i)| = 2. Biết rằng tập hợp các điểm biểu diễn các số phức z là một đường tròn. Tính bán kính r của đường tròn đó.
Hướng dẫn giải
Gọi M(x, y) là điểm biểu diễn số phức z = x + yi, Với x, y ∈ ℝ. Từ giả thiết ta có:
|zi – (2 + i)| = 2 ⇔ |−y − 2 + (x − 1)i| = 2 ⇔ (x – 1)2 + (y + 2)2 = 4
Vậy, tập hợp điểm M thuộc đường tròn tâm I(1; −2), bán kính bằng R = 2.
Câu 6. Cho các số phức z thỏa mãn 
. Biết rằng tập hợp các điểm biểu diễn các số phức z là một đường tròn. Xác định tâm của đường tròn đó.
Hướng dẫn giải
Gọi M (x, y) là điểm biểu diễn số phức z = x + yi, với x, y ∈ ℝ. Từ giả thiết ta có:
|x + yi – 1|+ |x − yi − 1| = 2
Vậy, tập hợp điểm M thuộc đường tròn tâm I(1; 0), bán kính bằng R = 1.
Dạng 9. Max – min của mô-đun số phức
Phương pháp giải
Tính toán mô-đun theo một ẩn, sau đó dùng khảo sát hàm số.
a) Dùng bất đẳng thức
Cauchy: Với a1, a2, …, an là các số thực không âm, ta luôn có:
Dấu “=” xảy ra khi a1 = a2 = … = an.
Bunhiacopxki: (a1b1 + a2b2) ≤ (a12 + a22)( b12 + b22). Dấu “=” xảy ra khi 
||z1| – |z2|| ≤ |z1 + z2| ≤ |z1| + |z2|.
b) Dùng hình học
+) Cho ∆: ax + by + c = 0 và điểm M(x0; y0). Điểm H ∈ ∆ sao cho MH nhỏ nhất thì H là hình chiếu vuông góc của M trên ∆.
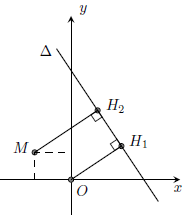
Tọa độ H1 = ∆ ⋂ OH1; H2 = ∆ ⋂ MH2
+) Cho (C) có tâm I(a; b), bán kính R và điểm M (x0; y0). Xét điểm H ∈ (C).
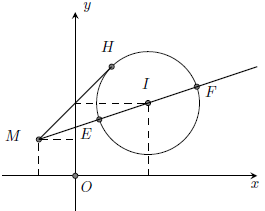
Khi đó:
MHmin khi H trùng E. Suy ra: ME = |IM – R|
MHmax khi H trùng F. Suy ra MF = |IM +R|
Bài tập vận dụng
Câu 1. Trong tất cả các số z có dạng z = (a – 3) + (2 – a)i với a là số thực, hãy tìm số phức z có mô-đun nhỏ nhất?
Hướng dẫn giải
Dấu “=” xảy ra khi 
Vậy 
Câu 2. Xét tất cả các số phức z thỏa mãn |z + 2 – 2i| = |z – 4i|. Tìm mô-đun nhỏ nhất của số phức ω = iz +1.
Hướng dẫn giải
Xét các số phức z = x + yi, với x, y ∈ ℝ có điểm biểu diễn là M(x, y). Khi đó:
+) |z + 2 – 2i| = |z – 4i| = |x + 2 + (y − 2)i| = |x + (y – 4)i| ⇔ x + y = 2 ⇔ y = 2 – x
+) ω = iz + 1 = 1 – y + xi
+) 
. Dấu bằng xảy ra khi 
Câu 3. Cho số phức z thỏa mãn |z – 3 + 4i| = 4. Tìm giá trị lớn nhất và nhỏ nhất của |z|.
Hướng dẫn giải
Ta có |z – 3 + 4i| = 4 nên tập hợp điểm M biểu diễn ở thuộc đường trong tâm I(3; −4), bán kính R = 4.
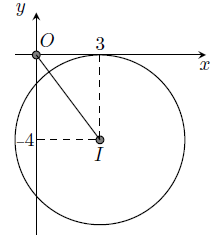
Ta có: |z| = OM. Bài toán trở thành “Tìm điểm M ∈ (C) sao cho OMmin“.
Tính 
.
Vậy 
Câu 4. Trong các số phức z thỏa mãn điều kiện 
, tìm số phức có mô-đun nhỏ nhất.
Hướng dẫn giải
Xét các số phức z = x + yi, với x, y ∈ ℝ có điểm biểu diễn là M (x, y).
Từ điều kiện , suy ra M thuộc đường tròn (C) có tâm I(2; −3), bán kính R = 
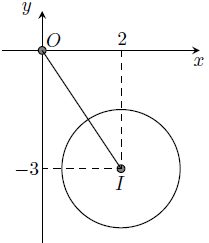
Ta có: |z| = OM. Bài toán trở thành “Tìm điểm M ∈ (C) sao cho OMmin“.
Phương trình 
M = OI ∩ (C), với xM < 2. Suy ra, tọa độ 
Câu 5. Với hai số phức z1, z2 thỏa mãn z1 + z2 = 8 + 6i và |z1 – z2| = 2, tìm giá trị lớn nhất K của biểu thức P = |z1| + |z2|.
Hướng dẫn giải
Xét hình bình hành OACB như hình vẽ
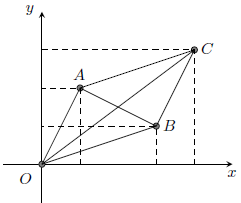
Điểm A, B lần lượt biểu diễn cho số phức z1, z2. Khi đó:
OA = |z1|, OB = |z2|, OC = |z1 + z2|, AB = |z1 – z2|
Ta luôn có:
|z1 + z2|2 + |z1 − z2|2 = 2 (|z1|2 + |z2|2)
Từ giả thiết: |z1 − z2| = 2; |z1 + z2| = 10. Suy ra: |z1|2 + |z2|2 = 52
Từ đó, ta có: 
Dấu bằng xảy ra khi 
hoặc 
.
Vậy 
Câu 6. Xét các số phức z thỏa mãn |z – 1 − i| + |z − 7 – 4i| = 
. Gọi a, b lần lượt là giá trị lớn nhất và nhỏ nhất của |z – 5 + 2i|. Tính a + b.
Hướng dẫn giải
Trong mặt phẳng tọa độ, xét các điểm A(1; 1), B(7; 4) và I(5; −2). Gọi M (x; y), với x, y ∈ ℝ là điểm biểu diễn số phức z = x + yi.
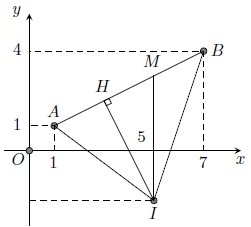
Khi đó: 
. Suy ra tập hợp điểm M biểu diễn số phức z thuộc đoạn AB
Theo hình vẽ: |z – 5 + 2i| = IM.
Vậy 
.
Bạn đang xem bài viết Tổng quan lý thuyết và một số dạng bài tập phổ biến xem thêm các bài viết khác về chủ đề Toán lớp 12. Chúc bạn 1 ngày vui vẻ!
