Toán lớp 10: Các dạng đặc trưng và cách giải mới nhất 2023

Bạn đang xem bài viết Các dạng đặc trưng và cách giải. Hi vọng sẽ là đáp án bạn ưng ý. Cùng theo dõi nhé!

Để giải được bất phương trình chứa căn thức chúng ta cần vận dụng nhiều kỹ năng như biến đổi căn thức, xét dấu đa thức, … Và đây là một trong những dạng toán có khá nhiều biến thể mà các bạn học sinh cần lưu ý.

Trong bài viết này, Cấp Nước Lào Cai sẽ giúp bạn đọc tìm hiểu chi tiết một số dạng bất phương trình căn thức thường gặp và cách giải có logic nhất. Từ đó bạn sẽ không cảm thấy khó khăn ở phần này nữa và việc giải quyết các bài toán cũng nhanh chóng và chính xác hơn.

Tóm tắt

Biến đổi phương trình và bất phương trình chứa căn

$\sqrt {f\left( x \right)} = g\left( x \right){\text{ }}\left( 1 \right)$ . Ta có: $\left( 1 \right) \Leftrightarrow \left\{ \begin{gathered} f\left( x \right) \geqslant 0 \hfill \\ g\left( x \right) \geqslant 0 \hfill \\ f\left( x \right) = {g^2}\left( x \right) \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} g\left( x \right) \geqslant 0 \hfill \\ f\left( x \right) = {g^2}\left( x \right) \hfill \\ \end{gathered} \right.$

$\sqrt {f\left( x \right)} < g\left( x \right){\text{ }}\left( 2 \right)$ . Ta có: $\left( 2 \right) \Leftrightarrow \left\{ \begin{gathered} f\left( x \right) \geqslant 0 \hfill \\ g\left( x \right) \geqslant 0 \hfill \\ f\left( x \right) < {g^2}\left( x \right) \hfill \\ \end{gathered} \right.$

$\left( 3 \right) \Leftrightarrow \left[ \begin{gathered} \left\{ \begin{gathered} f\left( x \right) \geqslant 0 \hfill \\ g\left( x \right) < 0 \hfill \\ \end{gathered} \right. \hfill \\ \left\{ \begin{gathered} g\left( x \right) \geqslant 0 \hfill \\ f\left( x \right) > {g^2}\left( x \right) \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \right.$ . Ta có: $\\[\left( 3 \right) \Leftrightarrow \left[ \begin{gathered} \left\{ \begin{gathered} f\left( x \right) \geqslant 0 \hfill \\ g\left( x \right) < 0 \hfill \\ \end{gathered} \right. \hfill \\ \left\{ \begin{gathered} g\left( x \right) \geqslant 0 \hfill \\ f\left( x \right) > {g^2}\left( x \right) \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \right.\]$

Phân dạng bài tập

Dạng 1. Phương trình và bất phương trình chứa căn thức cơ bản

Câu 1. Giải các phương trình sau:

a) $\sqrt {6 - 4x + {x^2}} = x + 4$

b) $\sqrt {x + 5} - \sqrt {x - 3} = 2$

c) $\sqrt {3x + 4} + \sqrt {x + 4} = 2\sqrt x$

Hướng dẫn giải

a) Xét phương trình:

$\begin{gathered} \sqrt {6 - 4x + {x^2}} = x + 4 \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} 6 - 4x + {x^2} \geqslant 0 \hfill \\ x + 4 \geqslant 0 \hfill \\ 6 - 4x + {x^2} = {\left( {x + 4} \right)^2} \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} x \geqslant - 4 \hfill \\ 6 - 4x + {x^2} = {x^2} + 8x + 16 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} x \geqslant - 4 \hfill \\ x = - \frac{5}{6} \hfill \\ \end{gathered} \right. \Leftrightarrow x = - \frac{5}{6} \hfill \\ \end{gathered}$

b) Xét phương trình:

$\begin{gathered} \sqrt {x + 5} - \sqrt {x - 3} = 2 \hfill \\ \hfill \\ \Leftrightarrow \sqrt {x + 5} = 2 + \sqrt {x - 3} \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} x + 5 \geqslant 0 \hfill \\ x - 3 \geqslant 0 \hfill \\ x + 5 = 4 + x - 3 + 4\sqrt {x - 3} \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} x \geqslant 3 \hfill \\ 1 = \sqrt {x - 3} \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} x \geqslant 3 \hfill \\ x - 3 = 1 \hfill \\ \end{gathered} \right. \Leftrightarrow x = 4 \hfill \\ \end{gathered}$

c) Xét phương trình:

$\begin{gathered} \sqrt {3x + 4} + \sqrt {x + 4} = 2\sqrt x \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} 3x + 4 \geqslant 0 \hfill \\ x + 4 \geqslant 0 \hfill \\ x \geqslant 0 \hfill \\ 3x + 4 + x + 4 + 2\sqrt {\left( {3x + 4} \right)\left( {x + 4} \right)} = 4x \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} x \geqslant 0{\text{ }}\left( 1 \right) \hfill \\ 4 + \sqrt {\left( {3x + 4} \right)\left( {x + 4} \right)} = 0{\text{ }}\left( 2 \right) \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$

Rõ ràng VT (2) > 0, ∀x ≥ 0. Vậy hệ (1) (2) vô nghiệm.

Suy ra phương trình đã cho vô nghiệm.

Câu 2. Giải các phương trình sau:

a) $3{x^2} + 15x + 2\sqrt {{x^2} + 5x + 1} = 2$

b) $\sqrt {{x^2} + x + 4} + \sqrt {{x^2} + x + 1} = \sqrt {2{x^2} + 2x + 9}$

c) $\frac{4}{{x + \sqrt {{x^2} + x} }} - \frac{1}{{x - \sqrt {{x^2} + x} }} = \frac{3}{x}$

d) $\sqrt {x + 2\sqrt {x - 1} } + \sqrt {x - 2\sqrt {x - 1} } = 2$

e) $\sqrt {x + 3 - 4\sqrt {x - 1} } + \sqrt {x + 8 - 6\sqrt {x - 1} } = 1$

f) $\sqrt[3]{{x + 1}} - \sqrt[3]{{x - 1}} = \sqrt[6]{{{x^2} - 1}}$

Hướng dẫn giải

a) Xét phương trình:

$3{x^2} + 15x + 2\sqrt {{x^2} + 5x + 1} = 2$ (1)

Đặt y = x² + 5x, khi đó (1) có dạng:

$\begin{gathered} 3y + 2\sqrt {y + 1} = 2 \hfill \\ \hfill \\ \Leftrightarrow 2\sqrt {y + 1} = 2 - 3y \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} y + 1 \geqslant 0 \hfill \\ 2 - 3y \geqslant 0 \hfill \\ 4\left( {y + 1} \right) = {\left( {2 - 3y} \right)^2} \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} y \leqslant \frac{2}{3} \hfill \\ 4y + 4 = 4 - 12y + 9{y^2} \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} y \leqslant \frac{2}{3} \hfill \\ 9{y^2} - 16y = 0 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} y \leqslant \frac{2}{3} \hfill \\ \left[ \begin{gathered} y = 0 \hfill \\ y = \frac{{16}}{9} \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \right. \Leftrightarrow y = 0 \hfill \\ \end{gathered}$

Từ đó trở về biến cũ ta có:

${x^2} + 5x = 0 \Leftrightarrow \left[ \begin{gathered} x = 0 \hfill \\ x = - 5 \hfill \\ \end{gathered} \right.$

b) Xét phương trình:

$\sqrt {{x^2} + x + 4} + \sqrt {{x^2} + x + 1} = \sqrt {2{x^2} + 2x + 9}$ (1)

Đặt y = x² + x + 1, khi đó (1) có dạng:

$\begin{gathered} \sqrt {y + 3} + \sqrt y = \sqrt {2y + 7} \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} y \geqslant 0 \hfill \\ y + 3 + y + 2\sqrt {y\left( {y + 3} \right)} = 2y + 7 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} y \geqslant 0 \hfill \\ \sqrt {y\left( {y + 3} \right)} = 2 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} y \geqslant 0 \hfill \\ {y^2} + 3y - 4 \geqslant 0 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} y \geqslant 0 \hfill \\ \left[ \begin{gathered} y = 1 \hfill \\ y = - 4 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \right. \Leftrightarrow y = 1 \hfill \\ \end{gathered}$

Từ đó trở về biến cũ ta có:

${x^2} + x + 1 = 1 \Leftrightarrow {x^2} + x = 0 \Leftrightarrow \left[ \begin{gathered} x = 0 \hfill \\ x = - 1 \hfill \\ \end{gathered} \right.$

c) Xét phương trình:

$\frac{4}{{x + \sqrt {{x^2} + x} }} - \frac{1}{{x - \sqrt {{x^2} + x} }} = \frac{3}{x}$ (1)

$\begin{gathered} \Leftrightarrow \frac{{4\left( {\sqrt {{x^2} + x} - x} \right)}}{x} - \frac{{\sqrt {{x^2} + x} + x}}{x} = \frac{3}{x} \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} x \ne 0 \hfill \\ 5\sqrt {{x^2} + x} - 3x = 3 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} x \ne 0 \hfill \\ 5\sqrt {{x^2} + x} = 3 + 3x \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} x \ne 0 \hfill \\ 3x + 3 \geqslant 0 \hfill \\ 25\left( {{x^2} + x} \right) = 9{x^2} + 18x + 9 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} x \ne 0 \hfill \\ x \geqslant - 1 \hfill \\ 16{x^2} + 7x - 9 = 0 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} x \ne 0 \hfill \\ x \geqslant - 1 \hfill \\ \left[ \begin{gathered} x = - 1 \hfill \\ x = \frac{9}{{16}} \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$

Vậy nghiệm của phương trình đã cho là x = –1 và x = $\frac{9}{{16}}$

d) Xét phương trình:

$\sqrt {x + 2\sqrt {x - 1} } + \sqrt {x - 2\sqrt {x - 1} } = 2$ (1)

Ta có:

$\begin{gathered} \left( 1 \right) \Leftrightarrow \sqrt {{{\left( {\sqrt {x - 1} + 1} \right)}^2}} + \sqrt {{{\left( {\sqrt {x - 1} - 1} \right)}^2}} = 2 \hfill \\ \hfill \\ \Leftrightarrow \sqrt {x - 1} + 1 + \left| {\sqrt {x - 1} - 1} \right| = 2{\text{ }}\left( 2 \right) \hfill \\ \end{gathered}$

+) Nếu x ≥ 2, khi đó $\sqrt {x - 1} - 1 \geqslant 0$ . Vậy:

$\begin{gathered} \left( 2 \right) \Leftrightarrow \sqrt {x - 1} + 1 + \sqrt {x - 1} - 1 = 2 \hfill \\ \hfill \\ \Leftrightarrow \sqrt {x - 1} = 1 \Leftrightarrow x = 2 \hfill \\ \end{gathered}$

+) Nếu 1 ≤ x < 2, khi đó $\sqrt {x - 1} - 1 < 0$ . Vậy:

$\begin{gathered} \left( 2 \right) \Leftrightarrow \sqrt {x - 1} + 1 + 1 - \sqrt {x - 1} = 2 \hfill \\ \hfill \\ \Leftrightarrow 2 = 2 \Leftrightarrow 1 \leqslant x < 2 \hfill \\ \end{gathered}$

Vậy nghiệm của phương trình đã cho là 1 ≤ x ≤ 2

e) Xét phương trình:

$\sqrt {x + 3 - 4\sqrt {x - 1} } + \sqrt {x + 8 - 6\sqrt {x - 1} } = 1$ (1)

Ta có:

$\begin{gathered} \left( 1 \right) \Leftrightarrow \sqrt {{{\left( {\sqrt {x - 1} - 2} \right)}^2}} + \sqrt {{{\left( {\sqrt {x - 1} - 3} \right)}^2}} = 1 \hfill \\ \hfill \\ \Leftrightarrow \left| {\sqrt {x - 1} - 2} \right| + \left| {\sqrt {x - 1} - 3} \right| = 1{\text{ }}\left( 2 \right) \hfill \\ \end{gathered}$

+) Nếu x ≥ 10, khi đó $\sqrt {x - 1} - 3 \geqslant 0$ . Vậy:

$\begin{gathered} \left( 2 \right) \Leftrightarrow \sqrt {x - 1} - 2 + \sqrt {x - 1} - 3 = 1 \hfill \\ \hfill \\ \Leftrightarrow \sqrt {x - 1} = 3 \Leftrightarrow x = 10 \hfill \\ \end{gathered}$

+) Nếu x ≤ 5, khi đó $\sqrt {x - 1} - 2 \leqslant 0$ . Vậy:

$\begin{gathered} \left( 2 \right) \Leftrightarrow 2 - \sqrt {x - 1} + 3 - \sqrt {x - 1} = 1 \hfill \\ \hfill \\ \Leftrightarrow \sqrt {x - 1} = 2 \Leftrightarrow x = 5 \hfill \\ \end{gathered}$

+) Nếu 5 < x < 9, khi đó $2 < \sqrt {x - 1} < 3$ . Vậy:

$\begin{gathered} \left( 2 \right) \Leftrightarrow \sqrt {x - 1} - 2 + 3 - \sqrt {x - 1} = 1 \hfill \\ \hfill \\ \Leftrightarrow 1 = 1 \Leftrightarrow 5 < x < 9 \hfill \\ \end{gathered}$

Vậy nghiệm của phương trình đã cho là 5 ≤ x ≤ 10

f) Xét phương trình:

$\sqrt[3]{{x + 1}} - \sqrt[3]{{x - 1}} = \sqrt[6]{{{x^2} - 1}}$ (1)

Điều kiện là: ${x^2} - 1 \geqslant 0 \Leftrightarrow \left[ \begin{gathered} x \geqslant 1 \hfill \\ x \leqslant - 1 \hfill \\ \end{gathered} \right.$

Do nếu x₀ ≥ 1 là nghiệm của (1) thì –x₀ cũng là nghiệm của (1)

Vì thế tạm xét (1) với x ≥ 1

Khi x = 1, thì VP (1) = 0; VT (1) ≠ 0 ⇒ x = 1 không phải là nghiệm

Khi x > 1, thì $\sqrt[6]{{{x^2} - 1}} > 0$

Vậy $\left( 1 \right) \Leftrightarrow \sqrt[6]{{\frac{{{{\left( {x + 1} \right)}^2}}}{{{x^2} - 1}}}} - \sqrt[6]{{\frac{{{{\left( {x - 1} \right)}^2}}}{{{x^2} - 1}}}} = 1$

$\Leftrightarrow \sqrt[6]{{\frac{{{{\left( {x + 1} \right)}^2}}}{{{x^2} - 1}}}} - \sqrt[6]{{\frac{{{{\left( {x - 1} \right)}^2}}}{{{x^2} - 1}}}} - 1 = 0\left( 2 \right)$

Đặt $y = \sqrt[6]{{\frac{{x + 1}}{{x - 1}}}} > 0$ , thì (2) có dạng:

$\begin{gathered} y - \frac{1}{y} - 1 = 0 \hfill \\ \hfill \\ \Leftrightarrow {y^2} - y - 1 = 0 \hfill \\ \hfill \\ \Leftrightarrow y = \frac{{1 + \sqrt 5 }}{2}\left( {{\text{do }}y > 0} \right) \hfill \\ \hfill \\ \Leftrightarrow \sqrt[6]{{\frac{{x + 1}}{{x - 1}}}} = \frac{{1 + \sqrt 5 }}{2} \hfill \\ \hfill \\ \Leftrightarrow \frac{{x + 1}}{{x - 1}} = {k^6}{\text{ }}\left( {k = \frac{{1 + \sqrt 5 }}{2}} \right) \hfill \\ \hfill \\ \Leftrightarrow 1 + \frac{2}{{x - 1}} = {k^6} \Leftrightarrow \frac{2}{{x - 1}} = {k^6} - 1 \hfill \\ \hfill \\ \Leftrightarrow x = \frac{{{k^6} + 1}}{{{k^6} - 1}} \hfill \\ \end{gathered}$

Vậy phương trình đã cho có hai nghiệm là $x = \pm \frac{{{k^6} + 1}}{{{k^6} - 1}}$ với $k = \frac{{1 + \sqrt 5 }}{2}$

Câu 3. Giải các bất phương trình sau:

a) $\sqrt {{x^2} + 3x + 3} < 2x + 1$

b) $\sqrt {8 + 2x - {x^2}} < 6 - 3x$

c) $\sqrt {x + 3} + \sqrt {x + 2} - \sqrt {2x + 4} > 0$

d) $\sqrt {3{x^2} + 5x + 7} - \sqrt {3{x^2} + 5x + 2} > 1$

Hướng dẫn giải

a) Xét bất phương trình:

$\begin{gathered} \sqrt {{x^2} + 3x + 3} < 2x + 1 \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} {x^2} + 3x + 3 \geqslant 0{\text{ }}\left( 1 \right) \hfill \\ 2x + 1 \geqslant 0{\text{ }}\left( 2 \right) \hfill \\ {x^2} + 3x + 3 < {\left( {2x + 1} \right)^2}{\text{ }}\left( 3 \right) \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$

Do x² + 3x + 3 > 0, ∀x (vì ∆ = 9 – 12 < 0) nên

$\left( 1 \right)\left( 2 \right)\left( 3 \right)\left\{ \begin{gathered} x \geqslant - \frac{1}{2} \hfill \\ 3{x^2} + x - 2 > 0 \hfill \\ \end{gathered} \right. \Leftrightarrow x > \frac{2}{3}$

b) Xét bất phương trình:

$\sqrt {8 + 2x - {x^2}} < 6 - 3x$ (1)

Ta có:

$\begin{gathered} \left( 1 \right) \Leftrightarrow \left[ \begin{gathered} \left\{ \begin{gathered} 8 + 2x - {x^2} \geqslant 0 \hfill \\ 6 - 3x < 0 \hfill \\ \end{gathered} \right. \hfill \\ \left\{ \begin{gathered} 8 + 2x - {x^2} \geqslant 0 \hfill \\ 6 - 3x \geqslant 0 \hfill \\ 8 + 2x - {x^2} > {\left( {6 - 3x} \right)^2} \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left[ \begin{gathered} \left\{ \begin{gathered} - 2 \leqslant x \leqslant 4 \hfill \\ x > 2 \hfill \\ \end{gathered} \right. \hfill \\ \left\{ \begin{gathered} x \leqslant 2 \hfill \\ 5{x^2} - 19x + 14 < 0 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left[ \begin{gathered} 2 < x \leqslant 4 \hfill \\ 1 < x \leqslant 2 \hfill \\ \end{gathered} \right. \Leftrightarrow 1 < x \leqslant 4 \hfill \\ \end{gathered}$

c) Xét bất phương trình:

$\begin{gathered} \sqrt {x + 3} + \sqrt {x + 2} - \sqrt {2x + 4} > 0 \hfill \\ \hfill \\ \Leftrightarrow \sqrt {x + 3} + \sqrt {x + 2} > \sqrt {2x + 4} \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} x \geqslant - 2 \hfill \\ x + 3 + x + 2 + 2\sqrt {\left( {x + 3} \right)\left( {x + 2} \right)} > 2x + 4 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} x \geqslant - 2 \hfill \\ 1 + 2\sqrt {\left( {x + 3} \right)\left( {x + 2} \right)} > 0 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow x \geqslant - 2 \hfill \\ \end{gathered}$

d) Xét bất phương trình:

$\sqrt {3{x^2} + 5x + 7} - \sqrt {3{x^2} + 5x + 2} > 1$ (1)

Đặt y = 3x² + 5x + 2, khi đó từ (1) có:

$\begin{gathered} \sqrt {y + 2} - \sqrt y > 1 \hfill \\ \hfill \\ \Leftrightarrow \sqrt {y + 2} > 1 + \sqrt y \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} y \geqslant 0 \hfill \\ y + 2 > 1 + y + 2\sqrt y \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} y \geqslant 0 \hfill \\ 1 > 2\sqrt y \hfill \\ \end{gathered} \right. \Leftrightarrow 0 \leqslant y \leqslant \frac{1}{4} \hfill \\ \end{gathered}$

Trở về biến cũ, ta có hệ sau:

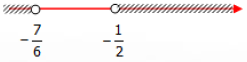
$\left\{ \begin{gathered} 3{x^2} + 5x + 2 \geqslant 0 \hfill \\ 3{x^2} + 5x + 2 \leqslant \frac{1}{4} \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} 3{x^2} + 5x + 2 \geqslant 0 \hfill \\ 12{x^2} + 20x + 7 \leqslant 0 \hfill \\ \end{gathered} \right.$

Biểu diễn trên trục số ta có:

Từ đó suy ra nghiệm cần tìm là: $- \frac{7}{6} \leqslant x \leqslant - 1$

Câu 4. Giải các bất phương trình sau:

a) $\frac{{1 - \sqrt {1 - 4{x^2}} }}{x} < 3$

b) $\frac{{1 - \sqrt {21 - 4x + {x^2}} }}{{x + 1}} \geqslant 0$

c) $\sqrt {2x + 4} - 2\sqrt {2 - x} > \frac{{12x - 8}}{{\sqrt {9{x^2} + 16} }}$

Hướng dẫn giải

a) Xét bất phương trình:

$\frac{{1 - \sqrt {1 - 4{x^2}} }}{x} < 3$ (1)

Chú ý x ≠ 0 và dùng phép nhân liên hợp ta có:

$\begin{gathered} \left( 1 \right) \Leftrightarrow \left\{ \begin{gathered} x \ne 0 \hfill \\ \frac{{\left( {1 - \sqrt {1 - 4{x^2}} } \right)\left( {1 + \sqrt {1 - 4{x^2}} } \right)}}{{x\left( {1 + \sqrt {1 - 4{x^2}} } \right)}} < 3 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} x \ne 0 \hfill \\ \frac{{4{x^2}}}{{x\left( {1 + \sqrt {1 - 4{x^2}} } \right)}} < 3 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} x \ne 0 \hfill \\ \frac{{4x}}{{1 + \sqrt {1 - 4{x^2}} }} < 3 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} x \ne 0 \hfill \\ 4x < 3\left( {1 + \sqrt {1 - 4{x^2}} } \right) \hfill \\ \end{gathered} \right.{\text{ }}\left( {{\text{do }}1 + \sqrt {1 - 4{x^2}} > 0} \right) \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} x \ne 0 \hfill \\ 4x - 3 < 3\sqrt {1 - 4{x^2}} \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$

$\begin{gathered} \Leftrightarrow \left[ \begin{gathered} \left\{ \begin{gathered} x \ne 0 \hfill \\ 1 - 4{x^2} \geqslant 0 \hfill \\ 4x - 3 < 0 \hfill \\ \end{gathered} \right. \hfill \\ \left\{ \begin{gathered} x \ne 0 \hfill \\ 4x - 3 \geqslant 0 \hfill \\ 9\left( {1 - 4{x^2}} \right) > {\left( {4x - 3} \right)^2} \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left[ \begin{gathered} \left\{ \begin{gathered} - \frac{1}{2} \leqslant x \leqslant \frac{1}{2} \hfill \\ x \ne 0 \hfill \\ \end{gathered} \right. \hfill \\ \left\{ \begin{gathered} x \geqslant \frac{3}{4} \hfill \\ 13{x^2} - 6x < 0 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} x \geqslant \frac{3}{4} \hfill \\ 0 < x < \frac{6}{{13}} \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$

Vì hệ $\left\{ \begin{gathered} x \geqslant \frac{3}{4} \hfill \\ 0 < x < \frac{6}{{13}} \hfill \\ \end{gathered} \right.$ vô nghiệm, nên suy ra nghiệm của (1) là $- \frac{1}{2} \leqslant x \leqslant \frac{1}{2}$ và x ≠ 0

b) Xét bất phương trình:

$\frac{{1 - \sqrt {21 - 4x + {x^2}} }}{{x + 1}} \geqslant 0$ (1)

$\Leftrightarrow \frac{{1 - 21 + 4x - {x^2}}}{{\left( {x + 1} \right)\left( {\sqrt {21 - 4x + {x^2}} + 1} \right)}} \geqslant 0$ (2)

Chú ý rằng x² – 4x + 21 > 0, ∀x ∈ ℝ (do ∆’ = 4 – 21 < 0)

Vì lẽ đó và do $1 + \sqrt {21 - 4x + {x^2}} > 0{\text{ }}\forall x \in \mathbb{R}$ , ta có:

$\begin{gathered} \left( 2 \right) \Leftrightarrow \frac{{ - {x^2} + 4x - 20}}{{x + 1}} \geqslant 0 \hfill \\ \hfill \\ \Leftrightarrow \frac{{{x^2} - 4x + 20}}{{x + 1}} \leqslant 0{\text{ }}\left( 3 \right) \hfill \\ \end{gathered}$

Lại do: x² – 4x + 20 > 0, ∀x ∈ ℝ (do ∆’ = 4 – 20 < 0), nên (3) ⇔ x + 1 < 0 ⇔ x < –1

c) Xét bất phương trình:

$\sqrt {2x + 4} - 2\sqrt {2 - x} > \frac{{12x - 8}}{{\sqrt {9{x^2} + 16} }}$ (1)

Thực hiện phép nhân liên hợp ta có:

$\begin{gathered} \frac{{\left( {2x + 4} \right) - 4\left( {2 - x} \right)}}{{\sqrt {2x + 4} + 2\sqrt {2 - x} }} > \frac{{2\left( {6x - 4} \right)}}{{\sqrt {9{x^2} + 16} }} \hfill \\ \hfill \\ \Leftrightarrow \frac{{6x - 4}}{{\sqrt {2x + 4} + 2\sqrt {2 - x} }} > \frac{{2\left( {6x - 4} \right)}}{{\sqrt {9{x^2} + 16} }} \hfill \\ \hfill \\ \Leftrightarrow \left( {3x - 2} \right)\left[ {\sqrt {9{x^2} + 16} - 2\left( {\sqrt {2x + 4} + 2\sqrt {2 - x} } \right)} \right] > 0 \hfill \\ \hfill \\ \Leftrightarrow \left( {3x - 2} \right)\left( {9{x^2} + 8x - 32 - 16\sqrt {8 - 2{x^2}} } \right) > 0 \hfill \\ \hfill \\ \Leftrightarrow \left( {3x - 2} \right)\left( {x - 2\sqrt {8 - 2{x^2}} } \right)\left( {8 + x + 2\sqrt {8 - 2{x^2}} } \right) > 0 \hfill \\ \hfill \\ \Leftrightarrow \left( {3x - 2} \right)\left( {x - 2\sqrt {8 - 2{x^2}} } \right) > 0 \hfill \\ \hfill \\ \Leftrightarrow \left[ \begin{gathered} \left\{ \begin{gathered} 3x - 2 > 0 \hfill \\ x - 2\sqrt {8 - 2{x^2}} > 0 \hfill \\ \end{gathered} \right. \hfill \\ \left\{ \begin{gathered} 3x - 2 < 0 \hfill \\ x - 2\sqrt {8 - 2{x^2}} < 0 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$

Giải hệ trên ta có:

$\left[ \begin{gathered} x > \frac{{\sqrt {32} }}{3} \hfill \\ 2 \leqslant x < \frac{2}{3} \hfill \\ \end{gathered} \right.$

Nhận xét:

Trong 3 Câu trên chúng ta đều sử dụng phương pháp nhân liên hợp để đơn giản quá trình giải.

Câu 5. Giải các bất phương trình sau:

a) $\sqrt {5 + x} - \sqrt { - x - 3} < - 1 + \sqrt {\left( {5 + x} \right)\left( { - x - 3} \right)}$

b) $\sqrt[3]{{2 - x}} + \sqrt {x - 1} > 1$

c) $\sqrt {{x^2} - 8x + 15} + \sqrt {{x^2} + 2x - 15} > \sqrt {4{x^2} - 18x + 18}$

Hướng dẫn giải

a) Xét bất phương trình:

$\begin{gathered} \sqrt {5 + x} - \sqrt { - x - 3} < - 1 + \sqrt {\left( {5 + x} \right)\left( { - x - 3} \right)} {\text{ }}\left( 1 \right) \hfill \\ \hfill \\ \Leftrightarrow \sqrt {5 + x} - \sqrt { - x - 3} + 1 - \sqrt {\left( {5 + x} \right)\left( { - x - 3} \right)} < 0 \hfill \\ \hfill \\ \Leftrightarrow \left( {\sqrt {5 + x} + 1} \right)\left( {1 - \sqrt { - x - 3} } \right) < 0{\text{ }}\left( 2 \right) \hfill \\ \end{gathered}$

Do 5 + x ≥ 0 khi x ≥ –5 (lúc đó $1 + \sqrt {5 + x} > 0$ ), nên

$\begin{gathered} \left( 2 \right) \Leftrightarrow \left\{ \begin{gathered} x \geqslant - 5 \hfill \\ 1 - \sqrt { - 3 - x} < 0 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} x \geqslant - 5 \hfill \\ \sqrt { - 3 - x} > 1 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} x \geqslant - 5 \hfill \\ - 3 - x > 1 \hfill \\ \end{gathered} \right. \Leftrightarrow - 5 \leqslant x < - 4 \hfill \\ \end{gathered}$

Đó là nghiệm của (1).

b) Xét bất phương trình:

$\sqrt[3]{{2 - x}} + \sqrt {x - 1} > 1$ (1)

Điều kiện x ≥ 1. Đặt:

$y = \sqrt[3]{{2 - x}} \Leftrightarrow {y^3} = 2 - x \Leftrightarrow x = 2 - {y^3}$

Khi đó (1) có dạng:

$y + \sqrt {1 - {y^3}} > 1 \Leftrightarrow \sqrt {1 - {y^3}} > 1 - y{\text{ }}\left( 2 \right)$

Do x ≥ 1, nên $y = \sqrt[3]{{2 - x}} \leqslant 1$ . Vì thế:

$\begin{gathered} \left( 2 \right) \Leftrightarrow \left\{ \begin{gathered} y \leqslant 1 \hfill \\ 1 - {y^3} > 1 - 2y + {y^2} \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} y \leqslant 1 \hfill \\ {y^3} + {y^2} - 2y < 0 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} y \leqslant 1 \hfill \\ y\left( {{y^2} + y - 2} \right) \leqslant 0 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} 0 \leqslant y \leqslant 1 \hfill \\ y \leqslant - 2 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$

Trở về biến cũ ta có:

$\left[ \begin{gathered} 0 \leqslant \sqrt[3]{{2 - x}} \leqslant 1 \hfill \\ \sqrt[3]{{2 - x}} \leqslant - 2 \hfill \\ \end{gathered} \right. \Leftrightarrow \left[ \begin{gathered} 0 \leqslant 2 - x \leqslant 1 \hfill \\ 2 - x \leqslant - 8 \hfill \\ \end{gathered} \right. \Leftrightarrow \left[ \begin{gathered} 1 \leqslant x \leqslant 2 \hfill \\ x \geqslant 10 \hfill \\ \end{gathered} \right.$

Vậy nghiệm của (1) là 1 ≤ x ≤ 2 và x ≥ 10.

c) Xét bất phương trình:

$\sqrt {{x^2} - 8x + 15} + \sqrt {{x^2} + 2x - 15} > \sqrt {4{x^2} - 18x + 18} {\text{ }}\left( 1 \right)$

Ta có:

$\left( 1 \right) \Leftrightarrow \sqrt {\left( {x - 3} \right)\left( {x - 5} \right)} + \sqrt {\left( {x - 3} \right)\left( {x + 5} \right)}$ $> \sqrt {\left( {x - 3} \right)\left( {4x - 6} \right)} {\text{ }}\left( 2 \right)$

Miền xác định của (1) là $\left\{ \begin{gathered} \left( {x - 3} \right)\left( {x - 5} \right) \geqslant 0 \hfill \\ \left( {x - 3} \right)\left( {x + 5} \right) \geqslant 0 \hfill \\ \left( {x - 3} \right)\left( {4x - 6} \right) \geqslant 0 \hfill \\ \end{gathered} \right. \Leftrightarrow \left[ \begin{gathered} x \leqslant - 5 \hfill \\ x = 3 \hfill \\ x \geqslant 5 \hfill \\ \end{gathered} \right.$

+) Nếu x = 3 thì VT (2) = VP (2) = 0 ⇒ x = 3 loại

+) Nếu x > 5, khi đó $x - 3 > 0 \Rightarrow \sqrt {x - 3} > 0$ và

$\begin{gathered} \left( 2 \right) \Leftrightarrow \sqrt {x - 5} + \sqrt {x + 5} > \sqrt {4x - 6} \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} x \geqslant 5 \hfill \\ 2x + 2\sqrt {{x^2} - 25} > 4x - 6 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} x \geqslant 5 \hfill \\ \sqrt {{x^2} - 25} > x - 3 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \left( {{\text{do }}x \geqslant 5 \Rightarrow x - 3 > 0} \right) \hfill \\ \end{gathered}$

Từ đó ta có:

$\begin{gathered} \left( 2 \right) \Leftrightarrow \left\{ \begin{gathered} x \geqslant 5 \hfill \\ {x^2} - 25 > {x^2} - 6x + 9 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} x \geqslant 5 \hfill \\ 6x > 34 \hfill \\ \end{gathered} \right. \Leftrightarrow x > \frac{{17}}{3} \hfill \\ \end{gathered}$

+) Nếu x < –5, khi đó viết lại (2) dưới dạng:

$\sqrt {\left( {x - 3} \right)\left( {x - 5} \right)} + \sqrt {\left( {x - 3} \right)\left( {x + 5} \right)} > \sqrt {\left( {x - 3} \right)\left( {4x - 6} \right)} {\text{ }}\left( 3 \right)$

Vì $x < - 5 \Rightarrow 3 - x > 0 \Rightarrow \sqrt {3 - x} > 0$ và

$\begin{gathered} \left( 3 \right) \Leftrightarrow \sqrt {5 - x} + \sqrt { - x - 5} > \sqrt {6 - 4x} \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} x < - 5 \hfill \\ \sqrt {{x^2} - 25} > 3 - x \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} x < - 5 \hfill \\ x > \frac{{17}}{3} \hfill \\ \end{gathered} \right.{\text{ }}\left( {{\text{VN}}} \right) \hfill \\ \end{gathered}$

Vậy nghiệm của hệ phương trình đã cho là $x > \frac{{17}}{3}$

Dạng 2. Quy phương trình chứa căn thức về hệ phương trình không chứa căn thức

Câu 1. Giải phương trình sau:

$\sqrt[3]{{x - 2}} + \sqrt[3]{{x + 3}} = \sqrt[3]{{2x + 1}}{\text{ }}\left( 1 \right)$

Hướng dẫn giải

Đặt $u = \sqrt[3]{{x - 2}};{\text{ }}v = \sqrt[3]{{x + 3}}$ , khi đó (1) có hệ sau:

$\begin{gathered} \left\{ \begin{gathered} u + v = \sqrt[3]{{{u^3} + {v^3}}}{\text{ }}\left( 2 \right) \hfill \\ {u^3} - {v^3} = - 5{\text{ }}\left( 3 \right) \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} {u^3} + 3uv\left( {u + v} \right) + {v^3} = {u^3} + {v^3} \hfill \\ {u^3} - {v^3} = - 5 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} uv\left( {u + v} \right) = 0 \hfill \\ {u^3} - {v^3} = - 5 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left[ \begin{gathered} \left\{ \begin{gathered} u = 0 \hfill \\ v = \sqrt[3]{5} \hfill \\ \end{gathered} \right. \hfill \\ \left\{ \begin{gathered} u = 0 \hfill \\ v = - \sqrt[3]{5} \hfill \\ \end{gathered} \right. \hfill \\ \left\{ \begin{gathered} u + v = 0 \hfill \\ {u^3} - {v^3} = - 5 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \right. \Leftrightarrow \left[ \begin{gathered} \left\{ \begin{gathered} x - 2 = 0 \hfill \\ x + 3 = 5 \hfill \\ \end{gathered} \right. \hfill \\ \left\{ \begin{gathered} x + 3 = 0 \hfill \\ x - 2 = - 5 \hfill \\ \end{gathered} \right. \hfill \\ {u^3} = - {v^3} = - \frac{5}{2} \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left[ \begin{gathered} x = 2 \hfill \\ x = - 3 \hfill \\ x - 2 = - \frac{5}{2} \hfill \\ \end{gathered} \right. \Leftrightarrow \left[ \begin{gathered} x = 2 \hfill \\ x = - 3 \hfill \\ x = - \frac{1}{2} \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$

Vậy (1) có các nghiệm x = 2; x = –3; x = $- \frac{1}{2}$

Câu 2. Giải phương trình sau:

$2\left( {{x^2} + 2} \right) = 5\sqrt {{x^3} + 1} {\text{ }}\left( 1 \right)$

Hướng dẫn giải

Viết lại (1) dưới dạng tương đương sau:

$2\left( {{x^2} + 2} \right) = 5\sqrt {x + 1} \cdot \sqrt {{x^2} - x + 1} {\text{ }}\left( 2 \right)$

Đặt $u = \sqrt {x + 1} ;{\text{ }}v = \sqrt {{x^2} - x + 1}$ , với điều kiện x ≥ –1

Khi đó ta có: x² + 2 = u² + v²

Vậy từ (2) có:

$\begin{gathered} 2\left( {{u^2} + {v^2}} \right) = 5uv \hfill \\ \hfill \\ \Leftrightarrow 2{u^2} + 2{v^2} - 5uv = 0 \hfill \\ \hfill \\ \Leftrightarrow \left( {2u - v} \right)\left( {2v - u} \right) = 0 \hfill \\ \hfill \\ \Leftrightarrow \left[ \begin{gathered} u = 2v \hfill \\ v = 2u \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} \sqrt {{x^2} - x + 1} = 2\sqrt {x + 1} \hfill \\ \sqrt {x + 1} = 2\sqrt {{x^2} - x + 1} \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left[ \begin{gathered} \left\{ \begin{gathered} {x^2} - 5x - 3 = 0 \hfill \\ x \geqslant - 1 \hfill \\ \end{gathered} \right. \hfill \\ \left\{ \begin{gathered} 4{x^2} - 5x + 3 = 0 \hfill \\ x \geqslant - 1 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \right. \Leftrightarrow \left[ \begin{gathered} x = \frac{{5 \pm \sqrt {37} }}{2} \hfill \\ {\text{VN}} \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$

Vậy nghiệm của (1) là $x = \frac{{5 \pm \sqrt {37} }}{2}$

Chú ý:

Tương tự ta có bài toán giải phương trình:

$2\left( {{x^2} - 3x + 2} \right) = 3\sqrt {{x^3} + 8}$

Bằng cách đặt $u = \sqrt {{x^2} - 2x + 4} \geqslant 0$ ; $v = \sqrt {x + 2} \geqslant 0$

Khi đó x² – 3x + 2 = u² – v²

Vậy ta dẫn đến:

$\begin{gathered} 2\left( {{u^2} - {v^2}} \right) = 3uv \hfill \\ \hfill \\ \Leftrightarrow \left( {u - 2v} \right)\left( {v + 2u} \right) = 0 \hfill \\ \hfill \\ \Leftrightarrow u = 2v\left( {{\text{do }}2u + v > 0} \right) \hfill \\ \hfill \\ \Rightarrow \sqrt {{x^2} - 2x + 4} = 2\sqrt {x + 2} \Leftrightarrow \left[ \begin{gathered} x = 3 + \sqrt {13} \hfill \\ x = 3 - \sqrt {13} \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$

Câu 3. Giải phương trình sau:

${\left( {\sqrt {{x^2} + 1} - x} \right)^5} + {\left( {\sqrt {{x^2} + 1} + x} \right)^5} = 123{\text{ }}\left( 1 \right)$

Hướng dẫn giải

Đặt $u = \sqrt {{x^2} + 1} - x;{\text{ }}v = \sqrt {{x^2} + 1} + x$

Từ (1) suy ra hệ: $\left\{ \begin{gathered} {u^5} + {v^5} = 123{\text{ }}\left( 2 \right) \hfill \\ uv = 1{\text{ }}\left( 3 \right) \hfill \\ \end{gathered} \right.$

Ta có: u⁵ + v⁵

= (u³ + v³)(u² + v²) – u²v²(u + v) (do uv = 1)

= (u³ + v³)(u² + v²) – (u + v)

= [(u + v)³ – 3uv(u + v)][(u + v)² – 2uv] – (u + v)

Vì thế

$\left( 2 \right)\left( 3 \right) \Leftrightarrow \left\{ \begin{gathered} {\left( {u + v} \right)^5} - 5{\left( {u + v} \right)^3} + 5\left( {u + v} \right) - 123 = 0{\text{ }}\left( 4 \right) \hfill \\ uv = 1{\text{ }}\left( 5 \right) \hfill \\ \end{gathered} \right.$

Đặt t = u + v, khi đó:

(4) ⇔ t⁵ – 5t³ + 5t – 123 = 0

⇔ (t – 3)(t⁴ + 3t³ + 4t² +12t + 41) = 0 (6)

Mặt khác $t = u + v = 2\sqrt {{x^2} + 1} > 0$ , do đó từ (6) có

(4) ⇔ t – 3 = 0 ⇔ t = 3

Vậy $\left( 4 \right)\left( 5 \right) \Leftrightarrow \left\{ \begin{gathered} u + v = 3 \hfill \\ uv = 1 \hfill \\ \end{gathered} \right.$

$\Leftrightarrow 2\sqrt {{x^2} + 1} = 3 \Leftrightarrow {x^2} = \frac{5}{4} \Leftrightarrow x = \pm \frac{{\sqrt 5 }}{2}$

Đó chính là nghiệm của (1).

Dạng 3. Sử dụng phương trình tương đương hoặc hệ quả để giải phương trình chứa căn thức

Câu 1. Giải phương trình sau:

$\sqrt[3]{{x - 2}} + \sqrt[3]{{x + 3}} = \sqrt[3]{{2x + 1}}{\text{ }}\left( 1 \right)$

Hướng dẫn giải

Ta có:

$\begin{gathered} \left( 1 \right) \Leftrightarrow \left( {x - 2} \right) + \left( {x + 3} \right) \hfill \\ \hfill \\ \begin{array}{*{20}{c}} {}&{ + {\text{ }}3\left( {\sqrt[3]{{x - 2}} + \sqrt[3]{{x + 3}}} \right)\sqrt[3]{{\left( {x - 2} \right)\left( {x + 3} \right)}} = 2x + 1} \end{array} \hfill \\ \hfill \\ \Leftrightarrow \sqrt[3]{{\left( {x - 2} \right)\left( {x + 3} \right)}}\left( {\sqrt[3]{{x - 2}} + \sqrt[3]{{x + 3}}} \right) = 0 \hfill \\ \hfill \\ \Leftrightarrow \left[ \begin{gathered} x - 2 = 0 \hfill \\ x + 3 = 0 \hfill \\ \sqrt[3]{{x - 2}} + \sqrt[3]{{x + 3}} = 0 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left[ \begin{gathered} x = 2 \hfill \\ x = - 3 \hfill \\ x - 2 = - \left( {x + 3} \right) \hfill \\ \end{gathered} \right. \Leftrightarrow \left[ \begin{gathered} x = 2 \hfill \\ x = - 3 \hfill \\ x = - \frac{1}{2} \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$

Vậy (1) có 3 nghiệm x = 2; x = –3; x = $- \frac{1}{2}$

Chú ý: Trong Câu này ta đã sử dụng phép biến đổi tương đương để giải (1).

Câu 2. Giải phương trình sau:

$\sqrt[3]{{2x - 1}} + \sqrt[3]{{x - 1}} = \sqrt[3]{{3x + 1}}{\text{ }}\left( 1 \right)$

Hướng dẫn giải

Ta có:

$\begin{gathered} \left( 1 \right) \Leftrightarrow \left( {2x - 1} \right) + \left( {x - 1} \right) \hfill \\ \hfill \\ \begin{array}{*{20}{c}} {}&{ + {\text{ }}3\sqrt[3]{{\left( {2x - 1} \right)\left( {x - 1} \right)}}\left( {\sqrt[3]{{2x - 1}} + \sqrt[3]{{x - 1}}} \right) = 3x + 1} \end{array} \hfill \\ \hfill \\ \Leftrightarrow \sqrt[3]{{\left( {2x - 1} \right)\left( {x - 1} \right)}}\left( {\sqrt[3]{{2x - 1}} + \sqrt[3]{{x - 1}}} \right) = 1{\text{ }}\left( 2 \right) \hfill \\ \end{gathered}$

Thay (1) vào (2), ta được phương trình hệ quả sau đây:

$\sqrt[3]{{\left( {2x - 1} \right)\left( {x - 1} \right)}} \cdot \sqrt[3]{{3x + 1}} = 1{\text{ }}\left( 3 \right)$

Bây giờ (3) ⇔ (2x − 1)(x − 1)(3x + 1) = 1

(4) ⇔ 6x³ − 7x² = 0 ⇔ x = 0 ∨ x = $\frac{7}{6}$

Do (3) là hệ quả của (1), nên thay x = 0 vào (1), ta có:

$\left\{ \begin{gathered} {\text{VT}}\left( 1 \right) = \sqrt[3]{{ - 1}} + \sqrt[3]{{ - 1}} = - 2 \hfill \\ {\text{VP}}\left( 1 \right) = \sqrt[3]{1} = 1 \hfill \\ \end{gathered} \right.$

Vậy x = 0 bị loại.

Thay x = $\frac{7}{6}$ vào (1), ta có:

$\left\{ \begin{gathered} {\text{VT}}\left( 1 \right) = \sqrt[3]{{\frac{8}{6}}} + \sqrt[3]{{\frac{1}{6}}} = \frac{3}{{\sqrt[3]{6}}} \hfill \\ \hfill \\ {\text{VP}}\left( 1 \right) = \sqrt[3]{{\frac{{27}}{6}}} = \frac{3}{{\sqrt[3]{6}}} \hfill \\ \end{gathered} \right.$

Vậy x = $\frac{7}{6}$ là nghiệm duy nhất của (1)

Chú ý: Trong Câu này:

(1) ⇔ (2)

(2) ⇒ (3)

(3) ⇔ (4)

Vậy (1) ⇒ (4). Do (4) là hệ quả của (1), nên sau khi có nghiệm x = 0; x = $\frac{7}{6}$ của (4), ta cần có phép thử lại.

Đây cũng là Câu chứng tỏ rằng, nếu sử dụng phương trình hệ quả mà không có phép thử lại, thì sẽ có thể dẫn đến việc thừa nghiệm.

Câu 3. Giải phương trình sau:

$\sqrt {2x + 3} + \sqrt {x + 1} = 3x + 2\sqrt {2{x^2} + 5x + 3} - 16{\text{ }}\left( 1 \right)$

Hướng dẫn giải

Đặt $u = \sqrt {2x + 3} + \sqrt {x + 1} \geqslant 1$

Ta có: ${u^2} = 3x + 4 + 2\sqrt {2{x^2} + 5x + 3}$ với u ≥ 0 (2)

Thay (1) vào (2) và dẫn đến phương trình hệ quả sau:

u² – 20 = u

⇔ u² – u – 20 = 0

⇔ u = 5 ∨ u = –4

⇔ u = 5 (do u ≥ 0)

Vậy (1) dẫn đến phương trình hệ quả sau:

$\begin{gathered} \sqrt {2x + 3} + \sqrt {x + 1} \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} x \geqslant - 1 \hfill \\ 3x + 4 + 2\sqrt {2{x^2} + 5x + 3} = 25 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} x \geqslant - 1 \hfill \\ \sqrt {2{x^2} + 5x + 3} = 21 - 3x \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} - 1 \leqslant x \leqslant 7 \hfill \\ {x^2} - 146x + 429 = 0 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} - 1 \leqslant x \leqslant 7 \hfill \\ \left[ \begin{gathered} x = 3 \hfill \\ x = 143 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \right. \Leftrightarrow x = 3 \hfill \\ \end{gathered}$

Thử lại x = 3 vào (1) thấy đúng, vậy (1) có nghiệm duy nhất x = 3.

Dạng 4. Hệ phương trình chứa căn thức

Câu 1. Giải các hệ phương trình sau:

a) $\left\{ \begin{gathered} \sqrt {x + y} + \sqrt {2x + y + 2} = 7 \hfill \\ 3x + 2y = 23 \hfill \\ \end{gathered} \right.$

b) $\left\{ \begin{gathered} x + y + \sqrt {x + y} = 20 \hfill \\ {x^2} + {y^2} = 136 \hfill \\ \end{gathered} \right.$

Hướng dẫn giải

a) Từ $\left\{ \begin{gathered} \sqrt {x + y} + \sqrt {2x + y + 2} = 7{\text{ }}\left( 1 \right) \hfill \\ 3x + 2y = 23{\text{ }}\left( 2 \right) \hfill \\ \end{gathered} \right.$

Ta có $\left( 1 \right)\left( 2 \right) \Leftrightarrow \left\{ \begin{gathered} \sqrt {x + y} + \sqrt {2x + y + 2} = 7{\text{ }}\left( 3 \right) \hfill \\ \left( {x + y} \right) + \left( {2x + y + 2} \right) = 25{\text{ }}\left( 4 \right) \hfill \\ \end{gathered} \right.$

Đặt $u = \sqrt {x + y} \geqslant 0;{\text{ }}v\sqrt {2x + y + 2} \geqslant 0$

Khi đó từ (3) (4) có hệ:

$\begin{gathered} \left\{ \begin{gathered} u + v = 7 \hfill \\ {\left( {u + v} \right)^2} - 2uv = 25 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} u + v = 7 \hfill \\ uv = 12 \hfill \\ \end{gathered} \right. \Leftrightarrow \left[ \begin{gathered} \left\{ \begin{gathered} u = 4 \hfill \\ v = 3 \hfill \\ \end{gathered} \right. \hfill \\ \left\{ \begin{gathered} u = 3 \hfill \\ v = 4 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left[ \begin{gathered} \left\{ \begin{gathered} x + y = 16 \hfill \\ 2x + y + 2 = 9 \hfill \\ \end{gathered} \right. \hfill \\ \left\{ \begin{gathered} x + y = 9 \hfill \\ 2x + y + 2 = 16 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \right. \Leftrightarrow \left[ \begin{gathered} x = - 9;y = 25 \hfill \\ x = 5;y = 4 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$

Vậy (1) (2) có hai nghiệm (–9, 25); (5, 4)

b) Từ $\left\{ \begin{gathered} x + y + \sqrt {x + y} = 20{\text{ }}\left( 1 \right) \hfill \\ {x^2} + {y^2} = 136{\text{ }}\left( 2 \right) \hfill \\ \end{gathered} \right.$

$\begin{gathered} \left( 1 \right) \Leftrightarrow {\left( {\sqrt {x + y} } \right)^2} + \sqrt {x + y} - 20 = 0 \hfill \\ \hfill \\ \Leftrightarrow \sqrt {x + y} = 4{\text{ }}\left( {{\text{do }}\sqrt {x + y} \geqslant 0} \right) \hfill \\ \hfill \\ \Leftrightarrow x + y = 16 \hfill \\ \end{gathered}$

Vậy $\left( 1 \right)\left( 2 \right) \Leftrightarrow \left\{ \begin{gathered} x + y = 16 \hfill \\ {x^2} + {y^2} = 136 \hfill \\ \end{gathered} \right.$

$\Leftrightarrow \left\{ \begin{gathered} x + y = 16 \hfill \\ {\left( {x + y} \right)^2} - 2xy = 136 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} x + y = 16 \hfill \\ xy = 60 \hfill \\ \end{gathered} \right.$

Vậy hệ (1) (2) có hai nghiệm (10, 6) và (6, 10).

Câu 2. Giải hệ phương trình sau:

$\left\{ \begin{gathered} \sqrt {\frac{{20y}}{x}} = \sqrt {x + y} + \sqrt {x - y} {\text{ }}\left( 1 \right) \hfill \\ \hfill \\ \sqrt {\frac{{16x}}{{5y}}} = \sqrt {x + y} + \sqrt {x - y} {\text{ }}\left( 2 \right) \hfill \\ \end{gathered} \right.$

Hướng dẫn giải

Điều kiện: $\left\{ \begin{gathered} x + y \geqslant 0 \hfill \\ x - y \geqslant 0 \hfill \\ x + y \geqslant x - y \hfill \\ xy > 0 \hfill \\ \end{gathered} \right. \Leftrightarrow x \geqslant y > 0$ . Khi đó:

$\begin{gathered} \left( 1 \right)\left( 2 \right) \Leftrightarrow \left\{ \begin{gathered} \sqrt {\frac{{20y}}{x}} = \sqrt {x + y} + \sqrt {x - y} \hfill \\ \hfill \\ 8 = \left( {x + y} \right) - \left( {x - y} \right) \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} \sqrt {\frac{{80}}{x}} = \sqrt {x + 4} + \sqrt {x - 4} \hfill \\ \hfill \\ y = 4;{\text{ }}x \geqslant 4 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} \frac{{80}}{x} = 2x + 2\sqrt {{x^2} - 16} \hfill \\ \hfill \\ y = 4;{\text{ }}x \geqslant 4 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} \frac{{40}}{x} - x = \sqrt {{x^2} - 16} \hfill \\ \hfill \\ y = 4;{\text{ }}x \geqslant 4 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} y = 4 \hfill \\ 4 \leqslant x \leqslant \sqrt {40} \hfill \\ \frac{{1600}}{{{x^2}}} + {x^2} - 80 = {x^2} - 16 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} y = 4 \hfill \\ 4 \leqslant x \leqslant \sqrt {40} \hfill \\ {x^2} = 25 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} y = 4 \hfill \\ x = 5 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$

Vậy nghiệm của hệ (1) (2) là (5, 4)

Câu 3. Giải hệ phương trình sau:

$\left\{ \begin{gathered} \sqrt {x + y} + \sqrt {x - y} = 4{\text{ }}\left( 1 \right) \hfill \\ {x^2} + {y^2} = 128{\text{ }}\left( 2 \right) \hfill \\ \end{gathered} \right.$

Hướng dẫn giải

Đặt $u = \sqrt {x + y} \geqslant 0;{\text{ }}v = \sqrt {x - y} \geqslant 0$

Ta có:

$\begin{gathered} \left\{ \begin{gathered} x + y = {u^2} \hfill \\ x - y = {v^2} \hfill \\ \end{gathered} \right. \Rightarrow \left[ \begin{gathered} x = \frac{1}{2}\left( {{u^2} + {v^2}} \right) \hfill \\ y = \frac{1}{2}\left( {{u^2} - {v^2}} \right) \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Rightarrow {x^2} + {y^2} = \frac{{{u^4} + {v^4}}}{2} \hfill \\ \end{gathered}$

Vậy từ (1) (2) ta có: $\left\{ \begin{gathered} u + v = 4{\text{ }}\left( 3 \right) \hfill \\ {u^4} + {v^4} = 256{\text{ }}\left( 4 \right) \hfill \\ \end{gathered} \right.$

Dễ thấy

$\begin{gathered} \left( 3 \right)\left( 4 \right) \Leftrightarrow \left[ \begin{gathered} u = 4;v = 0 \hfill \\ u = 0;v = 4 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left[ \begin{gathered} \left\{ \begin{gathered} x + y = 16 \hfill \\ x - y = 0 \hfill \\ \end{gathered} \right. \hfill \\ \left\{ \begin{gathered} x + y = 0 \hfill \\ x - y = 16 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \right. \Leftrightarrow \left[ \begin{gathered} x = 8;y = 8 \hfill \\ x = 8;y = - 8 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$

Vậy hệ (1) (2) có các nghiệm (8, 8); (8, –8)

Câu 4. Giải hệ phương trình sau:

$\left\{ \begin{gathered} \sqrt {{x^2} + x + y + 1} + x + \sqrt {{y^2} + x + y + 1} + y = 18{\text{ }}\left( 1 \right) \hfill \\ \sqrt {{x^2} + x + y + 1} - x + \sqrt {{y^2} + x + y + 1} - y = 18{\text{ }}\left( 2 \right) \hfill \\ \end{gathered} \right.$

Hướng dẫn giải

$\begin{gathered} \Leftrightarrow \left\{ \begin{gathered} \sqrt {{x^2} + x + y + 1} + \sqrt {{y^2} + x + y + 1} = 10 \hfill \\ x + y = 8 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} \sqrt {{x^2} + 9} + \sqrt {{y^2} + 9} = 10 \hfill \\ x + y = 8 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} {x^2} + {y^2} + 2xy = 64{\text{ }}\left( 3 \right) \hfill \\ {x^2} + {y^2} + 18 + 2\sqrt {{{\left( {xy} \right)}^2} + 9\left( {{x^2} + {y^2}} \right) + 81} = 100{\text{ }}\left( 4 \right) \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$

Từ (3) (4) suy ra:

$\begin{gathered} 2\sqrt {{{\left( {xy} \right)}^2} + 9\left( {64 - 2xy} \right) + 81} = 82 - 64 + 2xy \hfill \\ \hfill \\ \Leftrightarrow 2\sqrt {{{\left( {xy} \right)}^2} + 9\left( {64 - 2xy} \right) + 81} = 18 + 2xy{\text{ }}\left( 5 \right) \hfill \\ \end{gathered}$

Đặt xy = t, từ (5) có:

$\begin{gathered} \sqrt {{t^2} - 18t + 657} = 9 + t \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} t \geqslant - 9 \hfill \\ {t^2} - 18t + 657 = 81 + 18t + {t^2} \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} t \geqslant - 9 \hfill \\ t = 16 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$

Vậy đi đến hệ $\left\{ \begin{gathered} x + y = 8 \hfill \\ xy = 16 \hfill \\ \end{gathered} \right. \Leftrightarrow x = y = 4$

Vì thế nghiệm của (1) (2) là (4, 4)

Câu 5. Giải hệ phương trình sau:

$\left\{ \begin{gathered} \sqrt x + \sqrt y = 5{\text{ }}\left( 1 \right) \hfill \\ \sqrt {x + 5} + \sqrt {y + 5} = 8{\text{ }}\left( 2 \right) \hfill \\ \end{gathered} \right.$

Hướng dẫn giải

Điều kiện x ≥ 0, y ≥ 0. Ta có:

$\begin{gathered} \left( 1 \right)\left( 2 \right) \Leftrightarrow \left\{ \begin{gathered} \left( {\sqrt {x + 5} + \sqrt x } \right) + \left( {\sqrt {y + 5} + \sqrt y } \right) = 13 \hfill \\ \left( {\sqrt {x + 5} - \sqrt x } \right) + \left( {\sqrt {y + 5} - \sqrt y } \right) = 3 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} \left( {\sqrt {x + 5} + \sqrt x } \right) + \left( {\sqrt {y + 5} + \sqrt y } \right) = 13 \hfill \\ \frac{5}{{\sqrt {x + 5} + \sqrt x }} + \frac{5}{{\sqrt {y + 5} + \sqrt y }} = 3 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$

Đặt $u = \sqrt {x + 5} + \sqrt x ;{\text{ }}v = \sqrt {y + 5} + \sqrt y$ ta có hệ:

$\begin{gathered} \left\{ \begin{gathered} u + v = 13 \hfill \\ \frac{5}{u} + \frac{5}{v} = 3 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} u + v = 13 \hfill \\ uv = \frac{{65}}{{13}} \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} u = \frac{\begin{gathered} \hfill \\ 13 + \sqrt {\frac{{247}}{3}} \hfill \\ \end{gathered} }{2};v = \frac{\begin{gathered} \hfill \\ 13 - \sqrt {\frac{{247}}{3}} \hfill \\ \end{gathered} }{2} \hfill \\ u = \frac{\begin{gathered} \hfill \\ 13 - \sqrt {\frac{{247}}{3}} \hfill \\ \end{gathered} }{\begin{gathered} 2 \hfill \\ \hfill \\ \end{gathered} };v = \frac{\begin{gathered} \hfill \\ 13 + \sqrt {\frac{{247}}{3}} \hfill \\ \end{gathered} }{2} \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$

Chú ý: Ta phải có $u \geqslant \sqrt 5 ,v \geqslant \sqrt 5$ , nhưng $\frac{\begin{gathered} \hfill \\ 13 - \sqrt {\frac{{247}}{3}} \hfill \\ \end{gathered} }{2} < \sqrt 5$

Vậy hệ (1) (2) vô nghiệm

Câu 6. Giải hệ phương trình sau:

$\left\{ \begin{gathered} \sqrt {x + 1} + \sqrt {2 - y} = \sqrt 3 {\text{ }}\left( 1 \right) \hfill \\ \sqrt {2 - x} + \sqrt {y - 1} = \sqrt 3 {\text{ }}\left( 2 \right) \hfill \\ \end{gathered} \right.$

Hướng dẫn giải

Điều kiện −1 ≤ x ≤ 2, −1 ≤ y ≤ 2

Viết lại hệ (1) (2) dưới dạng tương đương sau:

$\begin{gathered} \left\{ \begin{gathered} \sqrt {x + 1} + \sqrt {2 - y} = \sqrt 3 \hfill \\ \left( {\sqrt {x + 1} - \sqrt {y + 1} } \right) - \left( {\sqrt {2 - x} - \sqrt {2 - y} } \right) = 0 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} \sqrt {x + 1} + \sqrt {2 - y} = \sqrt 3 \hfill \\ \frac{{x - y}}{{\sqrt {x + 1} - \sqrt {y + 1} }} + \frac{{x - y}}{{\sqrt {2 - x} - \sqrt {2 - y} }} = 0 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} \sqrt {x + 1} + \sqrt {2 - y} = \sqrt 3 \hfill \\ \left( {x - y} \right)\left[ {\frac{1}{{\sqrt {x + 1} - \sqrt {y + 1} }} + \frac{1}{{\sqrt {2 - x} - \sqrt {2 - y} }}} \right] = 0 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} - 1 \leqslant x \leqslant 2;{\text{ }} - 1 \leqslant y \leqslant 2 \hfill \\ x = y \hfill \\ \sqrt {x + 1} + \sqrt {2 - y} = \sqrt 3 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} - 1 \leqslant x \leqslant 2;{\text{ }} - 1 \leqslant y \leqslant 2 \hfill \\ x = y \hfill \\ 3 + 2\sqrt {\left( {x + 1} \right)\left( {2 - x} \right)} = 3 \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} y = x;{\text{ }} - 1 \leqslant x \leqslant 2 \hfill \\ \left[ \begin{gathered} x = - 1 \hfill \\ x = 2 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$

Vậy (1) (2) có hai nghiệm (–1, –1); (2, 2)

Dạng 5. Sử dụng phương pháp chiêu biến thiên hàm số để giải phương trình và bất phương trình chứa căn thức

Câu 1. Giải phương trình sau:

${x^5} + {x^3} - \sqrt {1 - 3x} + 4 = 0{\text{ }}\left( 1 \right)$

Hướng dẫn giải

Đặt $f\left( x \right) = {x^5} + {x^3} - \sqrt {1 - 3x} + 4$ , với $x \leqslant \frac{1}{3}$

Khi đó (1) có dạng f(x) = 0, với miền xác định $x \leqslant \frac{1}{3}$

Ta có: $f'\left( x \right) = 5{x^4} + 3{x^2} + \frac{3}{{2\sqrt {1 - 3x} }} > 0,{\text{ }}\forall x < \frac{1}{3}$

Vậy f(x) là hàm số đồng biến khi $x < \frac{1}{3}$

Ta có f(–1) = 0. Vậy x = –1 là nghiệm duy nhất của (1).

Câu 2. Giải phương trình sau:

$\sqrt {{x^2} + 15} = 3x - 2 + \sqrt {{x^2} + 8} {\text{ }}\left( 1 \right)$

Hướng dẫn giải

Viết lại (1) dưới dạng

$f\left( x \right) = 3x - 2 + \sqrt {{x^2} + 8} - \sqrt {{x^2} + 15} {\text{ }}\left( 2 \right)$

Hàm số f(x) xác định với mọi x thuộc ℝ. Xét hai khả năng sau:

+) Nếu $x \leqslant \frac{2}{3} \Rightarrow 3x - 2 \leqslant 0$ . Mặt khác:

$\sqrt {{x^2} + 8} - \sqrt {{x^2} + 15} < 0$

Vậy f(x) < 0 khi $x \leqslant \frac{2}{3} \Rightarrow x \leqslant \frac{2}{3}$ sẽ không thể là nghiệm của (2)

+) Nếu $x > \frac{2}{3}$ . Khi đó ta có:

$\begin{gathered} f'\left( x \right) = 3 + x\left[ {\frac{1}{{\sqrt {{x^2} + 8} }} - \frac{1}{{\sqrt {{x^2} + 15} }}} \right] > 0 \hfill \\ \hfill \\ \left( {{\text{do }}x > \frac{2}{3}} \right) \hfill \\ \end{gathered}$

Vậy f(x) là hàm đồng biến khi $x > \frac{2}{3}$ . Mặt khác f(1) = 0

Vậy x = 1 là nghiệm duy nhất của (1)

Câu 3. Giải bất phương trình sau:

$\sqrt {x + 9} > 5 - \sqrt {2x + 4} {\text{ }}\left( 1 \right)$

Hướng dẫn giải

Viết lại (1) dưới dạng

$f\left( x \right) = \sqrt {x + 9} + \sqrt {2x + 4} > 5{\text{ }}\left( 2 \right)$

Ta có: $f'\left( x \right) = \frac{1}{{2\sqrt {x + 9} }} + \frac{1}{{\sqrt {2x + 4} }} > 0,{\text{ }}\forall x > - 2$

Vậy f(x) là hàm đồng biến khi x ≥ −2, mặt khác ta có f(0) = 5.

Từ đó suy ra nghiệm của (2) là x > 0.

Câu 4. Giải phương trình sau:

$\sqrt {\left( {x + 2} \right)\left( {2x - 1} \right)} - 3\sqrt {x + 6} = 4 - \sqrt {\left( {x + 6} \right)\left( {2x - 1} \right)} - 3\sqrt {x + 2} {\text{ }}\left( 1 \right)$

Hướng dẫn giải

Viết lại (1) dưới dạng tương đương:

$f\left( x \right) = \sqrt {\left( {x + 2} \right)\left( {2x - 1} \right)} - 3\sqrt {x + 6}$ $+ \sqrt {\left( {x + 6} \right)\left( {2x - 1} \right)} - 3\sqrt {x + 2} = 4$

với miền xác định x ≥ $\frac{1}{2}$

$\Leftrightarrow f\left( x \right) = \left( {\sqrt {x + 6} + \sqrt {x + 2} } \right)\left( {\sqrt {2x - 1} - 3} \right) = 4{\text{ }}\left( 2 \right)$

Từ (2) suy ra $\sqrt {2x - 1} - 3 \geqslant 0$

Vậy mọi nghiệm (nếu có) của (1) đều lớn hơn hoặc bằng 5. Vì thế xét f(x) với x ≥ 5

Ta có $\sqrt {x + 6} + \sqrt {x + 2}$ và $\sqrt {2x - 1} - 3$ là các hàm đồng biến > 0 khi x ≥ 5

Vậy f(x) là hàm đồng biến khi x ≥ 5, mặt khác:

$f\left( 7 \right) = \left( {\sqrt {13} + 3} \right)\left( {\sqrt {13} - 3} \right) = 4$

Do đó x = 7 là nghiệm duy nhất của (1)

Câu 5. Giải hệ phương trình sau:

$\left\{ \begin{gathered} \sqrt x + \sqrt {2 - y} = \sqrt 2 {\text{ }}\left( 1 \right) \hfill \\ \sqrt y + \sqrt {2 - x} = \sqrt 2 {\text{ }}\left( 2 \right) \hfill \\ \end{gathered} \right.$

Hướng dẫn giải

Ta có:

$\left( 1 \right)\left( 2 \right) \Leftrightarrow \left\{ \begin{gathered} \sqrt x + \sqrt {2 - y} = \sqrt 2 {\text{ }}\left( 3 \right) \hfill \\ \sqrt x - \sqrt {2 - x} = \sqrt y - \sqrt {2 - y} {\text{ }}\left( 4 \right) \hfill \\ \end{gathered} \right.$