Bạn đang xem bài viết Lý thuyết, cách vẽ đồ thị & dạng toán thường gặp. Hi vọng sẽ là đáp án bạn ưng ý. Cùng theo dõi nhé!
Tiếp theo bài học hàm số bậc nhất, ở bài viết này Cấp Nước Lào Cai sẽ giúp bạn đọc tìm hiểu chi tiết lý thuyết và một số dạng bài tập đặc trưng của hàm số bậc 2. Một số kiến thức mà bạn đọc cần phải nắm chắc trong bài viết này như: Dạng đặc trưng hàm số bậc 2, đồ thị, phương trình hoành độ giao điểm.
Lý thuyết hàm số bậc hai
Định nghĩa
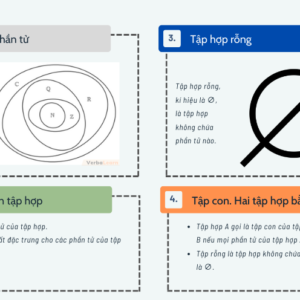
Hàm số bậc hai được cho bởi công thức y = ax2 + bx + c (a ≠ 0). Tập xác định của hàm số này là D = ℝ.
Đồ thị
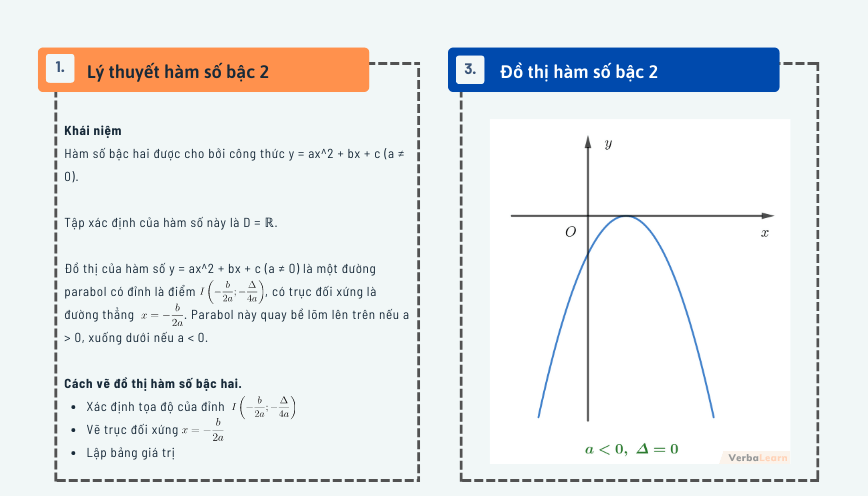
Đồ thị của hàm số y = ax2 + bx + c (a ≠ 0)là một đường parabol có đỉnh là điểm , có trục đối xứng là đường thẳng
. Parabol này quay bề lõm lên trên nếu a > 0, xuống dưới nếu a < 0.
Cách vẽ đồ thị hàm số bậc hai
– Xác định tọa độ của đỉnh
– Vẽ trục đối xứng
– Lập bảng giá trị

Đồ thị của hàm số y = ax2 + bx + c (a ≠ 0) cắt trục tung tại điểm (0; c).
Đồ thị của hàm số y = ax2 + bx + c (a ≠ 0) cắt trục hoành (nếu có) tại điểm có tọa độ (x0; 0) với x0 là nghiệm của phương trình ax2 + bx + c = 0.
– Vẽ Parabol
Khi vẽ cần chú ý đến dấu của hệ số a (a > 0 bề lõm quay lên trên, a < 0 bề lõm quay xuống dưới).
Sự biến thiên
Dựa vào đồ thị của hàm số y = ax2 + bx + c (a ≠ 0), Ta có: bảng biến thiên của nó trong hai trường hợp a > 0 và a < 0 như sau
– Với a > 0
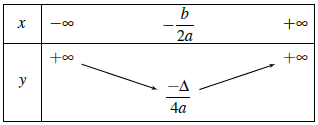
– Với a < 0
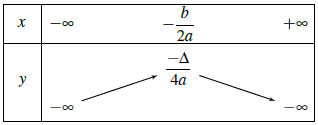
Định lý
Nếu a > 0 thì hàm số y = ax2 + bx + c nghịch biến trên khoảng , đồng biến trên khoảng
Nếu a < 0 thì hàm số y = ax2 + bx + c đồng biến trên khoảng , nghịch biến trên khoảng
Phương trình hoành độ giao điểm
Cho hàm số y = f(x) có đồ thị là (C1) và hàm số y = g(x) có đồ thị là (C2).
Khi đó, nếu M(x; y) là giao điểm của (C1) và (C2) thì tọa độ của M là nghiệm của hệ phương trình:
Phương trình (*) được gọi là phương trình hoành độ giao điểm của hai đồ thị (C1) và (C2). Và nếu giao điểm M có mang những đặc điểm, tính chất nào đó thì phương trình (*) cũng sẽ tồn tại những đặc điểm tương ứng với các đặc tính đó. Từ đây suy ra, để giải một bài toán về tính chất giao điểm của hai đồ thị (C1) và (C2), Ta có: thể tiến hành theo các bước sau:
– Lập phương trình hoành độ giao điểm của hai đồ thị (C1) và (C2) (tức là phương trình (*)).
– Biến đổi phương trình về dạng bậc hai đơn giản.
– Dựa vào điều kiện ban đầu của bài toán để chuyển về điều kiện cho phương trình hoành độ giao điểm.
Định lý Vi-ét
Cho phương trình bậc hai ax2 + bx + c = 0 (a ≠ 0).
– Nếu phương trình bậc hai có hai nghiệm x1 và x2 thì ta có:
– Phương trình có hai nghiệm trái dấu khi và chỉ khi P < 0.
– Phương trình có hai nghiệm dương phân biệt khi và chỉ khi:
– Phương trình có hai nghiệm âm phân biệt khi và chỉ khi:
– Phương trình có hai nghiệm phân biệt khác x0 khi và chỉ khi:
Công thức
Đồ thị của hàm số y = ax2 + bx + c (a ≠ 0) là một đường parabol có đỉnh là điểm
Đồ thị của hàm số y = ax2 + bx + c (a ≠ 0) cắt trục tung tại điểm (0; c) (lấy x = 0 thế vào hàm số).
Đồ thị của hàm số y = ax2 + bx + c (a ≠ 0) cắt trục hoành (nếu có) tại điểm có tọa độ (x0; 0) với x0 là nghiệm của phương trình: ax2 + bx + c = 0 (1). Số nghiệm của phương trình (1) là số giao điểm của đồ thị với trục hoành.
Phân dạng bài tập
Dạng 1. Vẽ đồ thị và lập bảng biến thiên của hàm số bậc hai
Phương pháp giải
Vẽ đồ thị của hàm số bậc hai ta thực hiện theo bốn bước như trên.
Để lập bảng biến thiên của hàm số bậc hai ta cần xem xét dấu của hệ số a, tính tọa độ của đỉnh và điền vào bảng thích hợp.
Bài tập vận dụng
Câu 1. Lập bảng biến thiên và vẽ đồ thị của hàm số y = x2 − 2x.
Hướng dẫn giải
Ta có: a = 1, b = −2, c = 0.
Suy ra tọa độ đỉnh là I(1; −1).
Vậy bảng biến thiên là
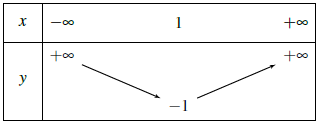
Do đó hàm số nghịch biến trên khoảng (−∞; 1) và đồng biến trên khoảng (1; +∞).
Vẽ đồ thị: Ta có đỉnh là I(1; −1) và trục đối xứng là x = 1.
Bảng giá trị
![]()
Ta có: đồ thị của hàm số y = x2 − 2x là
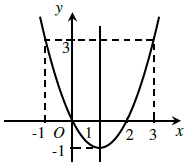
Câu 2. Lập bảng biến thiên và vẽ đồ thị của hàm số
Hướng dẫn giải
Ta có: a = , b = 2, c = −2. Suy ra tọa độ đỉnh là I(2; 0).
Vậy bảng biến thiên là
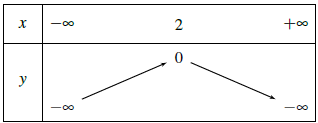
Do đó hàm số đồng biến trên khoảng (−∞; 2) và nghịch biến trên khoảng (2; +∞).
Vẽ đồ thị: Ta có đỉnh là I(2; 0) và trục đối xứng là x = 2.
Bảng giá trị
![]()
Ta có: đồ thị của hàm số là
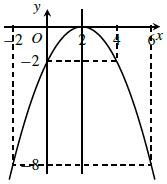
Câu 3. Lập bảng biến thiên và vẽ đồ thị của hàm số y = −3x2 + 2x − 1.
Hướng dẫn giải
Ta có: a = −3, b = 2, c = −1. Suy ra tọa độ đỉnh là
Vậy bảng biến thiên là
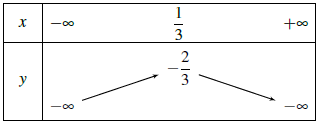
Do đó hàm số đồng biến trên khoảng và nghịch biến trên khoảng
Vẽ đồ thị: Ta có đỉnh là và trục đối xứng là
Bảng giá trị

Ta có: đồ thị của hàm số y = −3x2 + 2x − 1 là
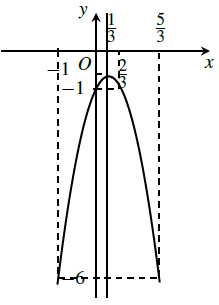
Câu 4. Lập bảng biến thiên và vẽ đồ thị của các hàm số sau:
a) y = −x2 + 2x + 3.
b) y = −x2 + 2x − 2.
c) y = 3x2 − 2x + 1.
d) y = −3x2 + 2x − 1.
Hướng dẫn giải
a) Đồ thị
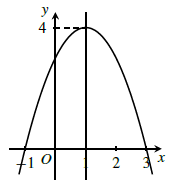
b) Đồ thị
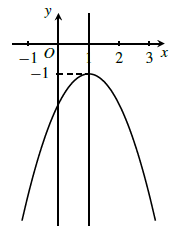
c) Đồ thị
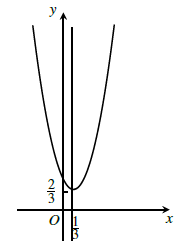
d) Đồ thị
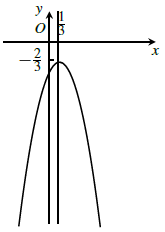
Câu 5. Cho hàm số y = −x2 + 2x + 3.
a) Lập bảng biến thiên và vẽ đồ thị (P) của hàm số.
b) Tìm các giá trị của x để y > 0 và y < 0.
Hướng dẫn giải
a) Đồ thị
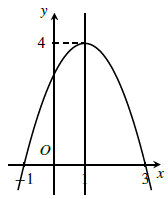
b) Để y > 0 thì x ∈ (−1; 3) và y < 0 thì x ∈ (−∞; −1) ∪ (3; +∞).
Câu 6. Cho hàm số y = x2 − 4x + 3.
a) Lập bảng biến thiên và vẽ đồ thị (P) của hàm số.
b) Tìm các giá trị của x để y > 0 và y < 0.
Hướng dẫn giải
a) Đồ thị
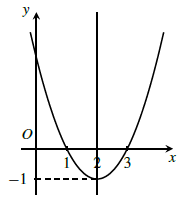
b) Để y > 0 thì x ∈ (−∞; 1) ∪ (3; +∞) và y < 0 thì x ∈ (1; 3).
Dạng 2. Tìm tọa độ của đỉnh và các giao điểm của parabol với các trục tọa độ. Tọa độ giao điểm giữa parabol (P) và một đường thẳng
Phương pháp giải
– Dựa vào các công thức cần nhớ để tìm tọa độ của đỉnh, giao điểm của parabol với các trục tọa độ. Tuy nhiên, khi tìm tọa độ của đỉnh I thì ta chỉ cần tìm hoành độ . Rồi sau đó thế x0 vào hàm số ban đầu để tìm
là tung độ của đỉnh I.
– Dựa vào phương trình hoành độ giao điểm để xác định giao điểm của parabol (P) với đường thẳng.
Bài tập vận dụng
Câu 1. Cho hàm số y = x2 − 4x + 3 có đồ thị là parabol (P). Tìm tọa độ của đỉnh, giao điểm của đồ thị với trục tung và trục hoành.
Hướng dẫn giải
Từ đề ta có: a = 1, b = −4, c = 3. Vậy hoành độ của đỉnh I là:
Vậy đỉnh I(2; −1).
Giao điểm của (P) và trục Oy: Cho x = 0 ⇒ y = 3. Vậy (P) cắt trục Oy tại điểm A(0; 3).
Giao điểm của (P) với trục Ox: Xét phương trình: x2 − 4x + 3 = 0 ⇔ x = 1 ∨ x = 3.
Vậy (P) cắt trục Ox tại hai điểm B(1; 0) và C(3; 0).
Câu 2. Cho hàm số y = −x2 − 3x + 1 có đồ thị là parabol (P). Tìm tọa độ của đỉnh, giao điểm của đồ thị với trục tung và trục hoành.
Hướng dẫn giải
Từ đề ta có: a = −1, b = −3, c = 1. Vậy hoành độ của đỉnh I là:
Vậy đỉnh .
Giao điểm của (P) và trục Oy: Cho x = 0 ⇒ y = 1. Vậy (P) cắt trục Oy tại điểm A(0; 1).
Giao điểm của (P) với trục Ox: Xét phương trình:
Vậy (P) cắt trục Ox tại hai điểm
Câu 3. Cho hàm số y = −x2 + x + 2 có đồ thị (P) và đường thẳng d: 4x + y − 3 = 0. Tìm giao điểm của đồ thị (P) và đường thẳng d.
Hướng dẫn giải
Đường thẳng d: y = −4x + 3. Xét phương trình hoành độ giao điểm:
Vậy đồ thị (P) và đường thẳng d cắt nhau tại hai điểm: A(0; 1) và B(5; 11).
Câu 4. Cho hàm số y = −x2 − x + 2 có đồ thị (P) và đường thẳng d: x – y + 3 = 0. Tìm giao điểm của đồ thị (P) và đường thẳng d.
Hướng dẫn giải
Đường thẳng d: y = x + 3. Xét phương trình hoành độ giao điểm:
−x2 − x + 2 = x + 3
⇔ x2 + 2x + 1 = 0
⇔ x = −1 ⇒ y = 2.
Vậy (P) và d tiếp xúc với nhau tại điểm A(−1; 2).
Câu 5. Tìm tọa độ đỉnh, giao điểm với trục tung, trục hoành (nếu có) của các parabol sau:
a) y = x2 + 4x − 1.
b)
Hướng dẫn giải
a) Tọa độ đỉnh I(−2; −5); giao điểm của parabol (P) với trục tung và trục hoành lần lượt là:
b) Tọa độ đỉnh I(2; −2); giao điểm của parabol (P) với trục tung là: A(0; −4); đồ thị không cắt trục hoành.
Câu 6. Tìm giao điểm của parabol (P) và đường thẳng d trong các trường hợp sau:
a) y = −x2 và y = x − 2.
b) và y = −3x + 3.
c) y = x2 − x − 3 và y = x − 4.
d) y = x2 + 6x + 4 và y = −x + 1.
Hướng dẫn giải
a) Số giao điểm của (P) và d là số nghiệm của phương trình:
Vậy (P) và d cắt nhau tại 2 điểm A(1; −1) và B(–2; –4).
b) (P) và d không cắt nhau.
c) (P) và d tiếp xúc với nhau tại A(1; −3).
d) (P) và d không cắt nhau.
Câu 7. Cho parabol (P): y = x2 − 4x + 3. Dùng (P) tìm tập hợp các giá trị của x để y ≤ 0.
Hướng dẫn giải
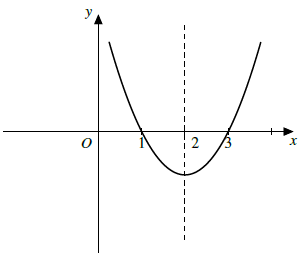
Từ hình vẽ ta có: 1 ≤ x ≤ 3.
Dạng 3. Dựa vào đồ thị biện luận theo m số giao điểm của parabol (P) và đường thẳng
Phương pháp giải
– Sử dụng đồ thị để biện luận số nghiệm của phương trình.
– Sử dụng phương trình hoành độ giao điểm để đưa bài toán tìm giao điểm về bài toán biện luận số nghiệm của phương trình.
Bài tập vận dụng
Câu 1. Cho parabol (P): y = x2 − x − 2. Dùng đồ thị (P), biện luận theo m số nghiệm của phương trình: x2 – x − (m − 2) = 0.
Hướng dẫn giải
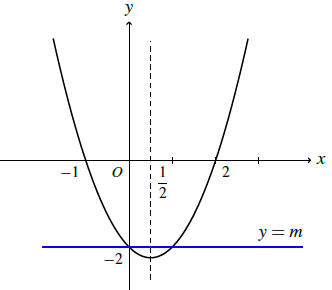
Xét phương trình: x2 – x − (m − 2) = 0 ⇔ x2 − x − 2 = m (1).
Nghiệm số của phương trình là hoành độ giao điểm của 2 đường parabol (P): y = x2 − x − 2 và đường thẳng ∆: y = m. Theo đồ thị ta có kết quả:
m < : (∆) và (P) không có điểm chung ⇒ phương trình (1) vô nghiệm.
m = : (∆) tiếp xúc với (P) ⇒ phương trình (1) có nghiệm kép.
m > : (∆) cắt (P) tại 2 điểm ⇒ phương trình (1) có 2 nghiệm phân biệt.
Câu 2. Cho parabol (P): y = x(2 − x) + 3 và đường thẳng d: y = −x + m. Định m để:
a) d cắt (P) tại hai điểm phân biệt.
b) d và (P) tiếp xúc.
c) d và (P) không có điểm chung.
Hướng dẫn giải
Phương trình hoành độ giao điểm của d và (P):
x(2 − x) + 3 = −x + m ⇔ x2 − 3x + m − 3 = 0 (1).
∆ = 9 − 4(m − 3) = −4m + 21
a) d cắt (P) tại hai điểm phân biệt ⇔ phương trình (1) có 2 nghiệm phân biệt:
⇔ ∆ = −4m + 21 > 0 ⇔ m <
b) d và (P) tiếp xúc ⇔ phương trình (1) có nghiệm kép:
⇔ ∆ = −4m + 21 = 0 ⇔ m =
c) d và (P) không có điểm chung ⇔ phương trình (1) vô nghiệm:
⇔ ∆ = −4m + 21 < 0 ⇔ m >
Câu 3. Cho hàm số: y = x2 − 2x − 3 có đồ thị là parabol (P) và đường thẳng d: y = 4x + m. Biện luận theo m số giao điểm của d và (P).
Hướng dẫn giải
HD: Sử dụng phương trình hoành độ giao điểm để đưa bài toán về biện luận theo m số nghiệm của phương trình.
Đáp số:
m > −12: d cắt (P) tại hai điểm phân biệt;
m = −12: d tiếp xúc với (P);
m < −12: d và (P) không có điểm chung.
Câu 4. Cho parabol và đường thẳng y = x + m. Với giá trị nào của m thì parabol và đường thẳng cắt nhau tại hai điểm phân biệt?
Hướng dẫn giải
m < 1 thì parabol và đường thẳng cắt nhau tại hai điểm phân biệt.
Câu 5. Cho parabol . Tìm giá trị của m và n để đường thẳng y = mx + n đi qua điểm (0; −1) và tiếp xúc với parabol.
Hướng dẫn giải
Đáp số: và
Câu 6. Cho hai parabol y = −x2 + 2x + 3 và . Tìm m để đường thẳng y = m cắt cả hai parabol.
Hướng dẫn giải
HD: Vẽ hai parabol trên 1 hệ trục tọa độ.
Đáp số: −5 ≤ m ≤ 4.
Dạng 4. Xác định hàm số bậc hai khi biết các yếu tố liên quan
Phương pháp giải
Ta thực hiện theo các bước sau.
Bước 1: Giả sử parabol (P): y = ax2 + bx + c với a ≠ 0.
Bước 2: Dựa vào giả thiết đề bài để xác định a, b, c.
Một số giả thiết thường gặp ở bước này và cách xử lí.
– Parabol đi qua điểm
– Parabol có trục đối xứng
– Parabol có đỉnh
– Parabol có giá trị nhỏ nhất (hoặc giá trị lớn nhất) bằng hoặc
Bước 3: Kết luận.
Bài tập vận dụng
Câu 1. Xác định parabol y = ax2 + bx + 3, biết rằng parabol đi qua hai điểm A(1; 2) và B(−2; 11).
Hướng dẫn giải
Parabol (P): y = ax2 + bx + 3 (a ≠ 0). Ta có: c = 3.
Vì (P) đi qua A(1; 2) nên 2 = a + b + 3 ⇔ a + b = −1 (1).
Vì (P) đi qua B(−2; 11) nên 11 = 4a − 2b + 3 ⇔ 4a − 2b = 8 (2).
Từ (1) và (2) ta có:
Vậy parabol (P): y = x2 − 2x + 3.
Câu 2. Cho parabol (P): y = −x2 + bx + c. Xác định b, c biết (P) đi qua điểm M(−2; 4) và có trục đối xứng x = −2.
Hướng dẫn giải
Parabol (P): y = −x2 + bx + c. Ta có: a = −1.
Vì (P) có trục đối xứng x = −2 nên
Vì M(−2; 4) ∈ (P) nên
4 = −(−2)2 + b.(−2) + c
⇔ 4 = −4 − 2b + c
⇔ −2b + c = 8.
Mà b = −4 nên 8 + c = 8 ⇔ c = 0.
Vậy (P): y = −x2 − 4x.
Câu 3. Cho parabol (P): y = ax2 − 2x + c. Xác định parabol (P) biết (P) có đỉnh I(1; −3).
Hướng dẫn giải
Parabol (P): y = ax2 − 2x + c. Ta có: b = −2.
Cách 1: Vì (P) có đỉnh I(1; −3) nên (P) có trục đối xứng x = 1.
Khi đó:
Hơn nữa, vì đỉnh I(1; −3) ∈ (P) nên −3 = 1⋅12 − 2⋅1 + c ⇔ c = −2.
Vậy (P): y = x2 − 2x − 2.
Cách 2: Vì (P) có đỉnh I(1; −3) nên
Vậy (P): y = x2 − 2x − 2.
Câu 4. Cho parabol (P): y = ax2 + bx + c. Xác định a, b, c biết (P) có giá trị nhỏ nhất bằng −5 và đi qua hai điểm M(1; −1), N(0; 4).
Hướng dẫn giải
Parabol (P): y = ax2 + bx + c (a ≠ 0).
Vì M(1; −1) ∈ (P) nên −1 = a + b + c (1).
Vì N(0; 4) ∈ (P) nên 4 = c (2).
Vì (P) có giá trị nhỏ nhất bằng −5 nên
Từ (1), (2) và (3), ta có:
Vậy (P1): y = x2 − 6x + 4 và (P2): y = 25x2 − 30x + 4.
Câu 5. Cho hàm số y = x2 − mx + m + 1 với m ∈ ℝ. Xác định m để đồ thị hàm số là parabol có đỉnh nằm trên đường thẳng y = x sao cho hoành độ đỉnh không âm.
Hướng dẫn giải
Với giá trị m cố định, gọi I(x0; y0) là đỉnh của parabol (x0 ≥ 0).
Khi đó:
Suy ra:
Vì đỉnh I nằm trên đường thẳng y = x nên y0 = x0
Vì x0 ≥ 0 nên m ≥ 0, do đó
Câu 6. Cho parabol (P): y = ax2 + bx + 4. Xác định a, b biết:
a) (P) đi qua hai điểm M(−1; 7) và N(−4; 4).
b) (P) có trục đối xứng x = 3 và đi qua điểm A(2; −4).
c) (P) có tung độ đỉnh bằng và cắt trục hoành tại điểm có hoành độ bằng 4.
Hướng dẫn giải
a) Thay tọa độ điểm M, N vào (P) ta có hệ phương trình
b) (P) có trục đối xứng x = 3 nên b = −6a.
Mà A(2; −4) ∈ (P) nên
−4 = 4a + 2b + 4
⇔ −8a = −8
⇔ a = 1.
Suy ra b = −6.
c) Hoành độ đỉnh
(P) cắt Ox tại điểm có tọa độ (4; 0) nên
Với b = 1 thì a = .
Với b = thì a =
.
Câu 7. Cho parabol (P): y = −x2 + bx + c. Xác định b, c biết:
a) (P) có đỉnh I(1; 4).
b) (P) đối xứng qua trục tung và có giá trị lớn nhất bằng 3.
c) (P) có hoành độ đỉnh bằng tung độ đỉnh và đi qua gốc tọa độ O.
Hướng dẫn giải
a) Vì (P) có đỉnh I(1; 4) nên
b) Vì (P) đối xứng qua trục tung nên
Mà (P) có giá trị lớn nhất bằng 3 nên
b2 − 4ac = −12a ⇔ 4c = 12 ⇔ c = 3.
c) Vì (P) đi qua gốc tọa độ O nên c = 0.
Mà hoành độ đỉnh bằng tung độ đỉnh nên
Câu 8. Cho parabol (P): y = ax2 + 3x + c. Xác định a, c biết:
a) (P) có hoành độ đỉnh bằng −1 và cắt trục tung tại điểm có tung độ bằng 4.
b) (P) có tung độ đỉnh gấp 2 lần hoành độ đỉnh và đi qua điểm A(1; 4).
c) (P) đạt giá trị nhỏ nhất bằng và đi qua gốc tọa độ O.
Hướng dẫn giải
a) Vì (P) cắt trục tung tại điểm (0; 4) nên c = 4.
Mà (P) có hoành độ đỉnh bằng −1 nên
b) Vì A(1; 4) ∈ (P) nên
a + 3 + c = 4 ⇔ a + c = 1 ⇔ a = 1 − c (1).
Mà (P) có tung độ đỉnh gấp 2 lần hoành độ đỉnh nên
Thay (1) vào (2) ta có:
c) Vì O ∈ (P) nên c = 0.
Mà (P) đạt giá trị nhỏ nhất bằng nên
Câu 9. Xác định parabol (P) biết:
a) (P) đi qua ba điểm A(1; 7), B(0; 5) và C(4; 1). (−x2 + 3x + 5)
b) (P) có trục đối xứng x = 3 và đi qua hai điểm M(−1; 0), N(0; 7).
c) (P) có đỉnh nằm trên trục hoành và đi qua hai điểm H(−2; 1), K(0; 9).
Hướng dẫn giải
a) (P) đi qua ba điểm A(1; 7), B(0; 5) và C(4; 1) nên ta có hệ phương trình:
b) (P) có trục đối xứng x = 3 nên b = −6a.
Mà (P) đi qua hai điểm M(−1; 0), N(0; 7) nên
Suy ra: b = 6.
c) Vì (P) có đỉnh nằm trên trục hoành nên
Mà (P) đi qua H(−2; 1), K(0; 9) nên
Do đó ta có:
Câu 10. Cho parabol (P): y = ax2 − 2ax + 2a với (a ≠ 0). Xác định a để (P) có đỉnh nằm trên đường thẳng 2x − y = 0.
Hướng dẫn giải
(P) có đỉnh I(1; a).
Vì I nằm trên đường thẳng 2x − y = 0 nên 2 − a = 0 ⇔ a = 2.
Câu 11. Xác định parabol (P) biết (P) có đỉnh I cách đều hai trục tọa độ, đi qua gốc tọa độ O(0; 0) và nhận x = làm trục đối xứng.
Hướng dẫn giải
Giả sử (P): y = ax2 + bx + c với a ≠ 0.
Vì (P) đi qua điểm O nên c = 0.
Vì (P) nhận x = làm trục đối xứng nên
Vì (P) cách đều hai trục tọa độ nên
Với b = 2 thì a = −2, với b = −2 thì a = 2.
Câu 12. Xác định parabol (P) biết (P) đi qua điểm A(0; 1) và có đỉnh I thuộc đường thẳng x + y − 3 = 0 sao cho độ dài đoạn IM ngắn nhất, biết M(−1; 3).
Hướng dẫn giải
Giả sử (P): y = ax2 + bx + c với a ≠ 0.
Gọi I(x0; y0) là đỉnh của parabol.
Vì I thuộc đường thẳng x + y − 3 = 0 nên y0 = 3 − x0. Do đó:
Vì với mọi x0 ∈ ℝ, nên IM ngắn nhất khi x0 =
.
Suy ra y0 = . Nên (P) có đỉnh
Vì A(0; 1) ∈ (P) nên c = 1. Hơn nữa ta có:
Dạng 5. Các bài toán liên quan đồ thị hàm số trị tuyệt đối của một hàm bậc hai
Phương pháp giải
Xét hàm số y = |ax2 + bx + c| có đồ thị là (P1). Để ý rằng:
nên để vẽ (P1), ta làm như sau.
a) Vẽ đồ thị (P) của hàm số y = ax2 + bx + c.
b) Giữ nguyên phần của (P) mà ở phía trên trục hoành.
c) Lấy đối xứng qua trục hoành đối với phần của (P) mà ở dưới trục hoành (sau đó bỏ đi phần của (P) mà ở dưới trục hoành).
Bài tập vận dụng
Câu 1. Biện luận theo tham số m số nghiệm của phương trình |x2 − 4x + 3| = m.
Hướng dẫn giải
Số nghiệm của phương trình bằng số giao điểm của đồ thị hàm số y = |x2 − 4x + 3| với đường thẳng (nằm ngang) y = m.
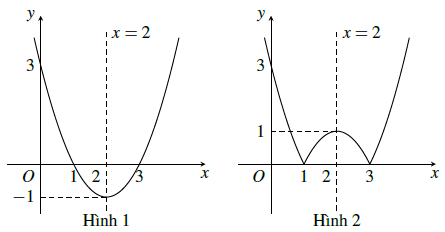
Ta vẽ (P): y = x2 − 4x + 3 (Hình 1).
Từ đó, ta suy ra đồ thị (P1) của hàm số y = |x2 − 4x + 3| (Hình 2).
Từ đồ thị (P2), ta có: kết luận như sau.
– m < 0: phương trình vô nghiệm.
– m = 0 hoặc m > 1: hai nghiệm.
– 0 < m < 1: 4 nghiệm.
– m = 1: 3 nghiệm.
Câu 2. Biện luận theo m số nghiệm của phương trình |x2 + 3x| = m.
Hướng dẫn giải
Giải tương tự ví dụ trên.
Đáp số:
– m < 0: phương trình vô nghiệm.
– m = 0 hoặc m > : hai nghiệm.
– 0 < m < : 4 nghiệm.
– m = : 3 nghiệm.
Dạng 6. Các bài toán liên quan đồ thị hàm số đối với trị tuyệt đối của biến
Phương pháp giải
Xét hàm số y = ax2 + b|x| + c. Khi x ≥ 0 hoặc x ≤ 0, hàm số trở thành hàm số bậc hai. Hơn nữa, hàm số đã cho là hàm số chẵn, nên đồ thị của nó nhận trục tung làm trục đối xứng.
Do đó, ta có thể vẽ đồ thị (P2) của hàm số y = ax2 + b|x| + c như sau.
a) Vẽ đồ thị (P) của hàm số y = ax2 + bx + c.
b) Bỏ phần của (P) ở bên trái trục tung. Sau đó lấy đối xứng qua trục tung đối với phần của (P) mà ở bên phải trục tung.
Lưu ý: Ta có: thể vẽ đồ thị hàm số y = ax2 + b|x| + c từ đồ thị hàm số y = ax2 – bx + c.
Bài tập vận dụng
Câu 1.
a) Vẽ đồ thị hàm số y = x2 − 4x + 3.
b) Tìm m để phương trình x2 − 4|x| + 3 = m có 4 nghiệm phân biệt.
Hướng dẫn giải
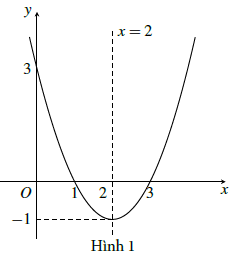
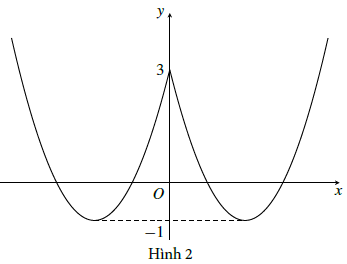
a) Xem hình 1.
b) Phương trình đã cho có 4 nghiệm phân biệt khi và chỉ khi đồ thị hàm số y = x2 − 4|x| + 3 và đường thẳng y = m.
Từ đồ thị hàm số y = x2 − 4x + 3 ở câu a), ta suy ra đồ thị của hàm số y = x2 − 4|x| + 3 như ở hình 2.
Từ đó, ta suy ra tất cả các giá trị m thỏa mãn yêu cầu bài toán là −1 < m < 3.
Câu 2. Tìm m để phương trình 2x2 − |x| = m có đúng 3 nghiệm.
Hướng dẫn giải
Giải tương tự ví dụ trên.
Đáp số: m = 0
Câu 3. Hỏi phương trình |2x2 − |x|| = m có tối đa bao nhiêu nghiệm?
Hướng dẫn giải
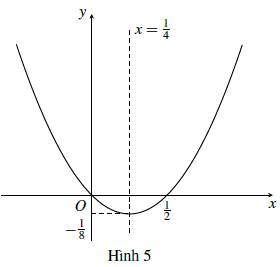
Ta vẽ đồ thị hàm số y = |2x2 − |x||.
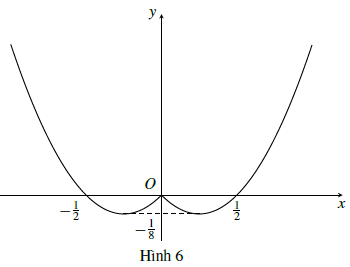
Trước hết, vẽ đồ thị hàm số y = 2x2 − x (hình 5), rồi suy ra đồ thị hàm số y = 2x2 − |x| (hình 6)
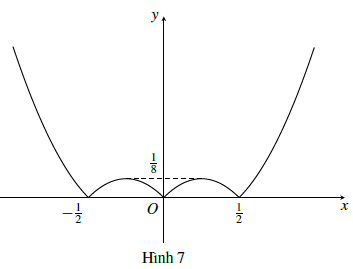
Từ đó, vẽ được đồ thị hàm số y = |2x2 − |x|| (hình 7).
Vậy phương trình đã cho có tối đa 6 nghiệm.
Dạng 7. Tính đơn điệu của hàm bậc hai
Phương pháp giải
Sự biến thiên của hàm số y = ax2 + bx + c (a ≠ 0).
– Tập xác định: D = ℝ.
– Nếu a > 0 thì hàm số nghịch biến (giảm) trên khoảng và đồng biến (tăng) trên khoảng
.
Bảng biến thiên
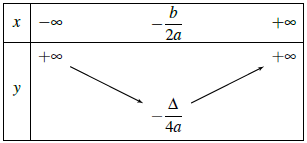
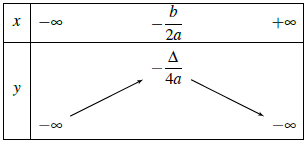
– Nếu a < 0 thì hàm số đồng biến (tăng) trên khoảng và nghịch biến (giảm) trên khoảng
.
Bảng biến thiên
Bài tập vận dụng
Câu 1. Xét sự biến thiên của hàm số y = x2 − 2x + 3.
Hướng dẫn giải
Tập xác định: D = ℝ.
Ta có: và
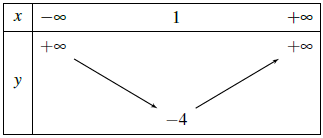
Do a = 1 > 0 nên hàm số nghịch biến trên khoảng (−∞; 1) và đồng biến trên khoảng (1; +∞).
Bảng biến thiên
Câu 2. Xét tính đơn điệu của hàm số y = −x2 + 2x − 3.
Hướng dẫn giải
Tập xác định: D = ℝ.
Ta có:
Do a = −1 < 0 nên hàm số đồng biến trên khoảng (−∞; 1) và nghịch biến trên khoảng (1; +∞).
Câu 3. Xét tính đơn điệu của hàm số y = x2 + 2|x|.
Hướng dẫn giải
Tập xác định: D = ℝ.
Ta có:
Mặt khác, hàm số y = x2 − 2x nghịch biến trên khoảng (−∞; 1) và đồng biến trên khoảng (1; +∞), hàm số y = x2 + 2x nghịch biến trên (−∞; −1) và đồng biến trên khoảng (−1; +∞).
Từ đó suy ra hàm số y = x2 + 2|x| nghịch biến khi x < 0 và đồng biến khi x ≥ 0.
Câu 4. Tìm tât cả các giá trị của tham số m để hàm số y = x2 + (m − 3)x + m đồng biến trên khoảng (1; +∞).
Hướng dẫn giải
Tập xác định: D = ℝ.
Ta có:
Để hàm số đồng biến trên khoảng (1; +∞) khi và chỉ khi
Vậy m ≥ 1.
Câu 5. Cho hàm số y = (m − 1)x2 + 4x − 5 với m ≠ 1. Tìm m sao cho hàm số đồng biến trên (1; 7).
Hướng dẫn giải
– Với m > 1 thì hàm số đồng biến trên khoảng .
Vậy, để hàm số đồng biến trên khoảng (1; 7) thì
Kết hợp điều kiện ta được m > 1.
– Với m < 1 thì hàm số đồng biến trên khoảng .
Vậy, để hàm số đồng biến trên (1; 7) thì
Tóm lại
Câu 6. Xét sự biến thiên của hàm số y = x2 − 6x − 5.
Hướng dẫn giải
Hàm số nghịch biến trên khoảng (−∞; 3) và đồng biến trên khoảng (3; +∞).
Câu 7. Xét tính đơn điệu của hàm số y = −x2 + 2017.
Hướng dẫn giải
Hàm số đồng biến trên khoảng (−∞; 0) và nghịch biến trên khoảng (0; +∞).
Câu 8. Xác định các khoảng đồng biến và nghịch biến của hàm số y = x|x − 2|.
Hướng dẫn giải
Ta có:
Mặt khác, hàm số y = −x2 + 2x đồng biến trên khoảng (−∞; 1) và nghịch biến trên khoảng (1; +∞), hàm số y = x2 − 2x nghịch biến trên (−∞; 1) và đồng biến trên khoảng (1; +∞).
Từ đó suy ra:
– Hàm số y = x|x − 2| đồng biến trên các khoảng (−∞; 1), [2; +∞).
– Hàm số y = x|x − 2| nghịch biến trên các khoảng (1; 2).
Câu 9. Tìm tất cả các giá trị của tham số m để hàm số y = −x2 + (2m − 3)x + 1 đồng biến trên khoảng (−∞; −5).
Hướng dẫn giải
Tập xác định: D = ℝ.
Ta có:
Do a = −1 < 0, nên để hàm số đồng biến trên khoảng (−∞; −5) khi và chỉ khi
Vậy m ≥ .
Câu 10. Cho hàm số y = (m − 1)x2 + 4x − 5 với m ≠ 1. Tìm m sao cho hàm số nghịch biến trên (−5; 2).
Hướng dẫn giải
– Với m < 1 thì hàm số nghịch biến trên khoảng .
Vậy, để hàm số nghịch biến trên khoảng (−5; 2) thì , điều này mâu thuẫn với điều kiện.
– Với m > 1 thì hàm số nghịch biến trên khoảng thì .
Vậy, để hàm số nghịch biến trên (−5; 2) thì , điều này mâu thuẫn với điều kiện.
Vậy không tồn tại giá trị của m.
Câu 11. Cho hàm số . Biện luận theo m số nghiệm của phương trình f(x) = m.
Hướng dẫn giải
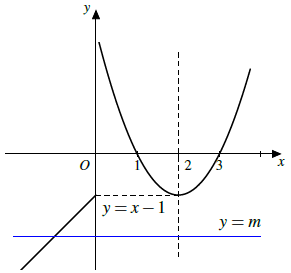
Dựa vào hình vẽ ta có:
– m ≤ −1: phương trình có 1 nghiệm;
– m > −1: phương trình có 2 nghiệm phân biệt.
Câu 12. Cho hàm số y = x2 − 2mx + m2 − 1 có đồ thị là (Cm). Chứng minh rằng (Cm) luôn cắt xx’ tại 2 điểm phân biệt A, B. Tìm m để A, B đối xứng nhau qua gốc tọa độ O.
Hướng dẫn giải
Để (Cm) luôn cắt Ox tại 2 điểm phân biệt thì ∆ > 0, ∀m.
Để A, B đối xứng nhau qua gốc tọa độ O thì m = 0.
Câu 13. Cho hàm số y = x2 − 4mx + 4m + 3 (Pm) với m ∈ ℝ. Viết phương trình đường thẳng d vuông góc với đường thẳng ∆: y = x − 1 và đi qua điểm cố định của họ parabol (Pm).
Hướng dẫn giải
Gọi M(x0; y0) là điểm cố định mà họ parabol (Pm) luôn đi qua.
Khi đó: ,với mọi m.
Suy ra: , với mọi m.
Nên
Vậy M(1; 4)
Vì d vuông góc với đường thẳng ∆: y = x − 1 nên d: y = −x + b, với b ≠ −1.
Mà M(1; 4) ∈ d nên 4 = −1 + b ⇔ b = 5.
Vậy d: y = −x + 5.
Câu 14. Cho hàm số y = x2 − (m − 1)x + m − 2 (Pm) với m ∈ ℝ. Tìm tất cả các giá trị của m để khoảng cách từ đỉnh của (Pm) đến trục hoành bằng .
Hướng dẫn giải
Với m tùy ý, gọi I(x0; y0) là đỉnh của (Pm).
Khi đó khoảng cách từ đỉnh của (Pm) đến trục hoành bằng
Theo giả thiết:
Câu 15.
a) Vẽ đồ thị hàm số y = x2 + 4x + 3.
b) Biện luận theo m số nghiệm của phương trình x2 − 4|x| + 3 = m.
Hướng dẫn giải
Gợi ý câu b). Ở bên trái trục tung, đồ thị hàm số y = x2 − 4|x| + 3 cũng chính là đồ thị của hàm số y = x2 + 4x + 3.
Hơn nữa, đồ thị hàm số y = x2 − 4|x| + 3 nhận trục tung làm trục đối xứng.
Câu 16. Tìm m để phương trình x|x − 1| = m có đúng 2 nghiệm.
Hướng dẫn giải
Số nghiệm của phương trình bằng với số giao điểm của đồ thị hàm số y = x|x − 2| + 1 và đường thẳng y = m.
Đồ thị hàm số y = x|x − 1| bao gồm hai phần: phần của parabol y = x(x − 2) + 1 với x ≥ 2, và phần của parabol y = x(2 − x) + 1 với x ≤ 2 (đường nét liền trong hình 8).
Từ đó, ta suy ra giá trị m phải tìm là m = 1 hoặc m = 2.
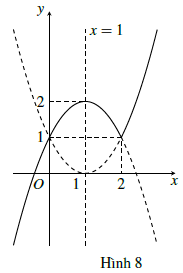
Bạn đang xem bài viết Lý thuyết, cách vẽ đồ thị & dạng toán thường gặp xem thêm các bài viết khác về chủ đề Toán lớp 10. Chúc bạn 1 ngày vui vẻ!