Bạn đang xem bài viết Lý thuyết và bài tập về các tập hợp số. Hi vọng sẽ là đáp án bạn ưng ý. Cùng theo dõi nhé!
Trong toán học, các phần tử tạo nên một tập hợp có thể là bất cứ loại dối tượng toán học nào. Vậy hiểu tập hợp trong toán học nghĩa là gì? Có những tập hợp số nào phổ biến? Cùng Cấp Nước Lào Cai tìm hiểu chi tiết trong bài viết sau đây nhé!
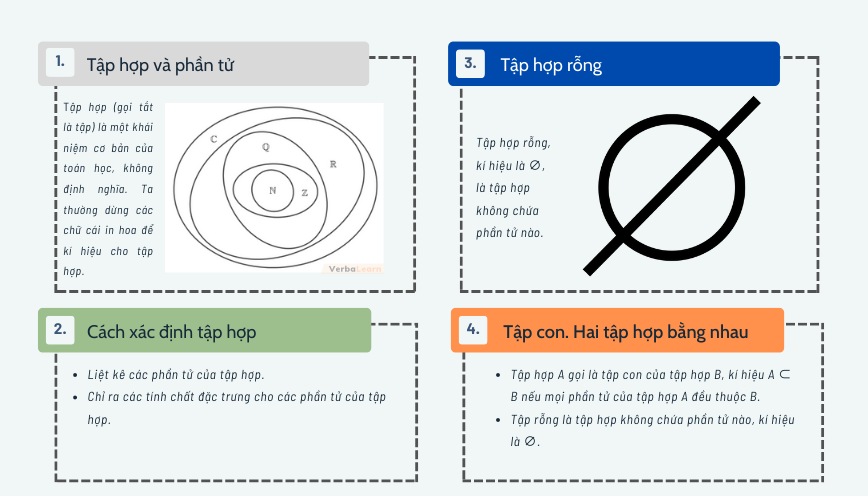
Lý thuyết tập hợp
Tập hợp và phần tử
– Tập hợp (gọi tắt là tập) là một khái niệm cơ bản của toán học, không định nghĩa.
– Ta thường dừng các chữ cái in hoa để kí hiệu cho tập hợp.
– Cho tập hợp A và phần tử x. Nếu x có mặt trong tập A ta nói x là một phần tử của tập A hay x thuộc A, kí hiệu x ∈ A hoặc A ∋ x. Nếu x không có mặt trong tập A ta nói x không thuộc A, kí hiệu x ∉ A hoặc A ∌ x.
Cách xác định tập hợp
– Liệt kê các phần tử của tập hợp.
– Chỉ ra các tính chất đặc trưng cho các phần tử của tập hợp.
Tập hợp rỗng
Định nghĩa 1: Tập hợp rỗng, kí hiệu là ∅, là tập hợp không chứa phần tử nào.
Tập con và hai tập hợp bằng nhau
– Tập hợp A gọi là tập con của tập hợp B, kí hiệu A ⊂ B nếu mọi phần tử của tập hợp A đều thuộc B.
Với kí hiệu đó, ta có A ⊂ B ⇔ (∀x, x ∈ A ⇒ x ∈ B)
– Tập rỗng là tập hợp không chứa phần tử nào, kí hiệu là ∅.
Qui ước: ∅ ⊂ A với mọi tập hợp A.
– Hai tập hợp A và B gọi là bằng nhau, kí hiệu A = B nếu mỗi phần tử của A là một phần tử của B và ngược lại. Với định nghĩa đó, ta có A = B ⇔ (A ⊂ B và B ⊂ A)
Tính chất
– ∅ ⊂ A, với mọi A.
– A ⊂ A, với mọi A
– Nếu A ⊂ B và B ⊂ C thì A ⊂ C
Phân dạng bài tập
Dạng 1. Xác định tập hợp – phần tử của tập hợp
Phương pháp giải
– Liệt kê các phần tử của tập hợp (giải phương trình nếu cần).
– Nêu đặc trưng của tập hợp.
Bài tập vận dụng
Câu 1. Xác định tập hợp A gồm 10 số nguyên tố đầu tiên bằng phương pháp liệt kê
Lời giải.
A = {2; 3; 5; 7; 11; 13; 17; 19; 23; 29}
Câu 2.
a) Tập hợp A các số thực lớn hơn 1 và nhỏ hơn 3 là A = {x ∈ ℝ | 1 < x < 3}.
b) Tập hợp S gồm các nghiệm của phương trình x8 + 9 = 0 là S = {x ∈ ℝ | x8 + 9 = 0}.
Câu 3. Liệt kê các phần tử của các tập hợp sau:
a) A = {n ∈ ℕ | n < 5}.
b) B là tập hợp các số tự nhiên lớn hơn 0 và nhỏ hơn 5.
c) C = {x ∈ ℝ | (x − 1)(x + 2) = 0}.
Lời giải.
a) A = {0; 1; 2; 3; 4}.
b) B = {1; 2; 3; 4}.
c) Ta có: (x − 1)(x + 2) = 0 ⇔ x = 1 ∨ x = –2
Mà x ∈ ℝ nên C = {−2; 1}.
Câu 4. Liệt kê các phần tử của các tập hợp sau:
a) A = {x ∈ ℤ | (2x2 − 3x + 1)(x + 5) = 0}.
b) B = {x ∈ Q | (x2 − 2)(x2 − 3x + 2) = 0}.
Lời giải.
a) Ta có:
Vì x ∈ ℤ nên A = {1; −5}.
b) Ta có:
Vì x ∈ Q nên B = {1; 2}.
Câu 5. Viết các tập hợp sau bằng phương pháp liệt kê:
a) A = {x ∈ Q | (x2 − 2x + 1)(x2 − 5) = 0}.
b) B = {x ∈ ℕ | 5 < n2 < 40}.
c) C = {x ∈ ℤ | x2 < 9}.
d) D = {x ∈ ℝ | |2x + 1| = 5}.
Lời giải.
a) A = {1}.
b) B = {3; 4; 5; 6}.
c) C = {−2; −1; 0; 1; 2}.
d) Ta có: |2x + 1| = 5 ⇔ x = 2 ∨ x = –3
Vậy C = {2; −3}.
Câu 6. Liệt kê các phần tử của mỗi tập hợp sau:
a) Tập hợp A các số chính phương không vượt quá 50.
b) Tập hợp B = {n ∈ ℕ | n(n + 1) ≤ 30}.
Lời giải.
A = {0; 1; 4; 9; 16; 25; 36; 49}
B = {1; 2; 3; 4; 5}
Câu 7. Viết các tập hợp sau bằng cách chỉ ra tính chất đặc trưng cho các phần tử của tập hợp đó.
a) A = {0; 4; 8; 12; 16; …; 52}.
b) B = {3; 6; 9; 12; 15; …; 51}.
c) C = {2; 5; 8; 11; 14; …; 62}.
Lời giải.
a) A = {x ∈ ℕ | 0 ≤ x ≤ 16 và x ⋮ 4}
b) B = {x ∈ ℕ | 3 ≤ x ≤ 51 và x ⋮ 3}
c) C = {x ∈ ℕ | 2 ≤ x ≤ 62 và (x − 2) ⋮ 3}
Câu 8. Viết các tập hợp sau bằng cách chỉ ra tính chất đặc trưng cho các phần tử của tập hợp đó.
a) A = {2; 3; 5; 7; 11; 13; 17}.
b) B = {−2; 4; −8; 16; −32; 64}.
Lời giải.
a) A = {x ∈ ℕ | x ≤ 17 và x là số nguyên tố}.
b) B = {x = (−2)n | n ∈ ℕ, 1 ≤ n ≤ 6}.
Câu 9. Tìm một tính chất đặc trưng xác định các phần tử của mỗi tập hợp sau
A = {1; 2; 3; 4; 5; 6; 7; 8; 9}
B = {0; 7; 14; 21; 28}
Lời giải.
A = {x ∈ ℕ*| x ≤ 9}
B = {x ∈ ℕ | x ⋮ 7 và x ≤ 28}
Câu 10. A là tập hợp các số nguyên tố nhỏ hơn 20. Liệt kê các phần tử của tập hợp A.
Lời giải.
A = {2; 3; 5; 7; 11; 13; 17; 19}.
Câu 11. Cho tập hợp A = {0; 2; 4; 6; 8; 10}. Hãy xác định tập hợp A bằng cách chỉ ra một tính chất đặc trưng cho các phần tử của nó.
Lời giải.
A là tập hợp các số tự nhiên chẵn nhỏ hơn hoặc bằng 10.
Câu 12. Cho A = {x ∈ ℕ | x là ước của 8}. Liệt kê các phần tử của tập hợp A.
Lời giải.
A = {1; 2; 4; 8}.
Câu 13. Cho A = {x ∈ ℤ | x là ước của 15}. Liệt kê các phần tử của tập hợp A.
Lời giải.
A = {−15; −5; −3; −1; 1; 3; 5; 15}.
Câu 14. Cho A = {x ∈ ℕ | x là ước chung của 30 và 20}.
Lời giải.
A = {1; 2; 5; 10}.
Câu 15. Cho A = {x ∈ ℕ | x là bội chung của 15 và 20, x ≤ 60}.
Lời giải.
A = {0; 30; 60}.
Câu 16. Viết các tập hợp sau bằng cách chỉ ra tính chất đặc trưng cho các phần tử của tập hợp đó.
a) A = {1; 2; 3; 4; 5; 6}.
b) B = {0; 2; 4; 5; 6; 8}.
Lời giải.
a) A = {x ∈ ℕ | 1 ≤ x ≤ 6}.
b) B = {x ∈ ℕ | x ⋮ 2 và x ≤ 8}.
Câu 17. Tìm một tính chất đặc trưng xác định các phần tử của mỗi tập hợp sau
a) A = {0; 2; 7; 14; 23; 34; 47}
b)
Lời giải.
A = {n2 − 2 | n ∈ ℕ, 1 ≤ n ≤ 7}
B = {x ∈ ℝ | x2 + 2x − 2 = 0}
Câu 18. Liệt kê các phần tử của mỗi tập hợp sau
a) A = {x ∈ ℤ | |x| < 8}
b)
Lời giải.
A = {−7; −6; −5; −4; −3; −2; −1; 0; 1; 2; 3; 4; 5; 6; 7}
B = {−5; −4; −3; 3; 4; 5}
Câu 19. Cho tập hợp X = {n ∈ ℕ | −5 < 5n + 2 < 303}. Tìm số phần tử của tập hợp X.
Lời giải.
−5 < 5n + 2 < 303 ⇔ −1 ≤ n ≤ 60.
Vậy số phần tử của tập hợp X là 62.
Câu 20. Liệt kê các phần tử của tập hợp A = x ∈ ℤ (x2 − 4x)(x4 − 6x2 + 5) = 0.
Lời giải.
Ta có:
Từ đó ta có A = {0; −1; 1; 4} chứa 4 phần tử.
Dạng 2. Tập hợp rỗng
Câu 1. Trong các tập hợp sau, tập hợp nào là tập hợp rỗng?
A = {x ∈ ℝ | x2 – x + 1 = 0}.
B = {x ∈ ℝ | 2x2 + 1 = 0}.
C = {x ∈ ℤ | |x| < 1}.
Lời giải.
Các tập hợp rỗng là A, B.
Câu 2. Tìm tất cả các giá trị thực của m để các tập hợp sau là tập hợp rỗng.
a) A = {x ∈ ℝ | x < m và x > 2m + 1}.
b) B = {x ∈ ℝ | x2 − 2x + m = 0}
Lời giải.
a) Để A là tập rỗng thì m ≥ 2m + 1 ⇔ m ≤ −1.
b) Để B là tập rỗng thì phương trình x2 − 2x + m = 0 phải vô nghiệm, tức là ∆’ = 1 − m < 0 ⇔ m > 1.
Câu 3. Trong các tập hợp sau, tập hợp nào là tập hợp rỗng?
Lời giải.
Tập hợp A, B.
Câu 4. Cho tập hợp A = {x ∈ ℕ | x = m}. Tìm m để A = ∅.
Lời giải.
Để A = ∅ thì m ∉ ℕ.
Câu 5. Tìm tất cả các giá trị nguyên của m để các tập hợp sau là tập hợp rỗng.
a) A = {x ∈ ℝ | x < m + 3 và x > 4m + 3}.
b) B = {x ∈ ℝ | x2 − 2x + m + 9 = 0}
Lời giải.
a) Để A là tập rỗng thì m + 3 ≥ 4m + 3 ⇔ m ≤ 0.
Vậy m thuộc tập hợp các số nguyên không dương.
b) Để B là tập rỗng thì phương trình x2 − 2x + m = 0 phải vô nghiệm, tức là ∆’ = −8 − m < 0 ⇔ m > −8.
Vậy m thuộc tập hợp các số nguyên lớn hơn −8.
Câu 6. Viết tập hợp sau dưới dạng liệt kê các phần tử.
a) A = {x ∈ ℤ | (x2 − 3x + 2)(2x2 + 3x + 1) = 0}.
b) B = {x ∈ ℕ | |x| < 3}.
Lời giải.
a) A = {1; 2; −1}.
b) B = {0; 1; 2}.
Câu 7. Tìm tất cả các giá trị của m để tập hợp A = {x ∈ ℕ | x < m} là tập hợp rỗng.
Lời giải.
Để A = ∅ thì m ≤ 0.
Câu 8. Cho A = {x ∈ ℕ | 1 < x−m < 3}. Tìm tất cả các giá trị của m để A = {1}.
Lời giải.
Để A = {1} thì 1 − m = 2 ⇔ m = −1.
Câu 9. Cho A = {x ∈ ℕ | −4 < x < 3}. Liệt kê tất cả các phần tử của A.
Lời giải.
Ta có A = {0; 1; 2}.
Câu 10. Tìm tất cả các giá trị của m để A = {x ∈ ℕ | 1 < x − m < 3} là tập hợp rỗng.
Lời giải.
Ta có: A = (m + 1; m + 3) ∩ ℕ.
Do đó, A = ∅ ⇔ m + 3 ≤ 0 ⇔ m ≤ −3.
Câu 11. Cho tập hợp ![]() . Tìm số nhỏ nhất của tập hợp A.
. Tìm số nhỏ nhất của tập hợp A.
Lời giải.
Ta có:
Đẳng thức xảy ra khi a = b = c. Vậy số nhỏ nhất là 1.
Dạng 3. Tập con. Tập bằng nhau
Phương pháp giải
– Tập hợp A là tập con của tập hợp B nếu mọi phần tử của A đều có trong B.
A ⊂ B ⇔ (∀x ∈ A ⇒ x ∈ B).
– ∅ ⊂ A, với mọi tập hợp A.
– A ⊂ A, với mọi tập hợp A.
– Có tập A gồm có n phần tử (n ∈ ℕ). Khi đó, tập A có 2n tập con.
–
Bài tập vận dụng
Câu 1. Tìm tất cả các tập con của tập A = {a, 1, 2}.
Lời giải.
Tập A có 23 = 8 tập con.
– 0 phần tử: ∅.
– 1 phần tử: {a}, {1}, {2}.
– 2 phần tử: {a, 1}, {a, 2}, {1, 2}.
– 3 phần tử: {a, 1, 2}.
Câu 2. Tìm tất cả các tập con có 2 phần tử của tập A = {1, 2, 3, 4, 5, 6}.
Lời giải.
{1, 2},{1, 3}, {1, 4}, {1, 5}, {1, 6}, {2, 3}, {2, 4}, {2, 5}, {2, 6}, {3, 4}, {3, 5}, {3, 6}, {4, 5}, {4, 6}, {5, 6}.
Câu 3. Xác định tập hợp X biết {1, 2} ⊂ X ⊂ {1, 2, 5}.
Lời giải.
Ta có:
– Vì {1, 2} ⊂ X nên tập hợp X có chứa các phần tử 1, 2.
– Vì X ⊂ {1, 2, 5} nên các phần tử của tập hợp X có thể là 1, 2, 5.
Khi đó tập hợp X có thể là {1, 2},{1, 2, 5}.
Câu 4. Xác định tập hợp X biết {a, 1} ⊂ X ⊂ {a, b, 1, 2}.
Lời giải.
Ta có:
– Vì {a, 1} ⊂ X nên tập hợp X có chứa 2 phần tử là a, 1.
– Vì X ⊂ {a, b, 1, 2} nên các phần tử của tập hợp X có thể là a, b, 1, 2.
Suy ra, tập hợp X có 2 phần tử, 3 phần tử hoặc 4 phần tử.
Khi đó, tập hợp X có thể là {a, 1},{a, 1, 2},{a, b, 1},{a, b, 2},{a, b, 1, 2}.
Câu 5. Cho ba tập hợp A = {2; 5}, B = {x; 5} và C = {x; y; 5}. Tìm các giá trị của x, y sao cho A = B = C.
Lời giải.
A = B ⇔ x = 2.
Khi x = 2, ta có C = {2; y; 5}.
Khi đó, ta có: {2; y; 5} ⊂ {2; 5} và {2; y; 5} ⊃ {2; 5}.
Từ đây, suy ra: y = 2 hoặc y = 5.
Vậy (x; y) = (2; 2) hoặc (x; y) = (2; 5) thỏa yêu cầu bài toán.
Câu 6. Cho hai tập hợp A = {x ∈ ℤ | x chia hết cho 3 và 2} và B = {x ∈ ℤ | x chia hết cho 6}. Chứng minh rằng A = B.
Lời giải.
Trước hết, ta cần chứng minh A ⊂ B. Thật vậy, với x ∈ A bất kì, ta luôn có x chia hết cho 2 và x chia hết cho 3.
Vì 2,3 là hai số nguyên tố cùng nhau nên x chia hết cho 6. Suy ra, x ∈ B.
Mặt khác, vì 6 = 2.3 nên với phần tử x ∈ B bất kì, ta luôn có x chia hết cho 2 và 3. Suy ra, x ∈ A.
Do đó, B ⊂ A.
Câu 7. Cho biết x là một phần tử của tập hợp A, xác định tính đúng sai của các mệnh đề sau:
a) x ∈
b) {x} ∈
c) x ⊂
d) {x} ⊂
Lời giải.
a) x ∈ A: đúng.
b) {x} ∈ A: sai về quan hệ giữa hai tập hợp.
c) x ⊂ A: sai về quan hệ giữa phần tử và tập hợp.
d) {x} ⊂ A: đúng.
Câu 8. Xác định tất cả các tập hợp con của mỗi tập hợp
a) A = {x; y}. b) B = {1; 2; 3}
Lời giải.
a) Các tập hợp con của tập hợp A = {x; y} là: ∅; {x}; {y}; {x; y}.
b) Các tập hợp con của tập hợp B = {1; 2; 3} là: ∅; {1}; {2}; {3}; {1; 2}; {1; 3}; {2; 3} và {1; 2; 3}.
Câu 9. Cho tập hợp A = {1; 2; 3; 4; 5; 6}. Tìm tất cả các tập con có 3 phần tử của tập hợp A sao cho tổng các phần tử này là một số lẻ.
Lời giải.
Để tổng của ba số nguyên là một số lẻ thì trong ba số chỉ có một số lẻ hoặc cả ba số đều lẻ.
Nói cách khác tập con này của A phải có một số lẻ hoặc ba số lẻ.
Chỉ có một tập con gồm ba số lẻ của A là {1; 3; 5}.
Các tập con gồm ba số của A trong đó có một số lẻ là: {1; 2; 4}; {1; 2; 6}; {1; 4; 6};{3; 2; 4}; {3; 2; 6}; {3; 4; 6}; {5; 2; 4}; {5; 2; 6}; {5; 4; 6}.
Câu 10. Trong hai tập hợp A và B dưới đây, tập hợp nào là tập con của tập hợp còn lại? Hai tập hợp A và B có bằng nhau không?
a) A là tập hợp các hình chữ nhật
B là tập hợp các hình bình hành.
b) A = {n ∈ ℕ | n là một ước chung của 12 và 18}
B = {n ∈ ℕ | n là một ước của 6}
Lời giải.
a) Tất cả các hình chữ nhật đều là hình bình hành nên A ⊂
b) A = {1; 2; 3; 6}; B = {1; 2; 3; 6}
Rõ ràng ta thấy A ⊂ B và B ⊂ A nên A = B.
Câu 11. Cho A = {n ∈ ℕ | n là ước của 2}; B = {x ∈ ℝ | (x2 − 1)(x − 2)(x − 4) = 0}. Tìm tất cả các tập hợp X sao cho A ⊂ X ⊂ B.
Lời giải.
Liệt kê các phần tử của tập hợp A và B ta được:
A = {1; 2}; B = {−1; 1; 2; 4}.
Muốn tìm tập X thỏa điều kiện A ⊂ X ⊂ B đầu tiên ta lấy X = A, sau đó ghép thêm các phần tử thuộc B mà không thuộc A. Với cách thực hiện như trên, ta có các tập hợp X thỏa mãn yêu cầu bài toán là: X = A = {1; 2}, rồi ghép thêm vào một phần tử ta được: {−1; 1; 2};{4; 1; 2}.
Ghép thêm vào A hai trong bốn phần tử còn lại của B ta được: X = B = {−1; 1; 2; 4}.
Câu 12. Cho A = {8k + 3 | k ∈ ℤ}; B = {2k + 1 | k ∈ ℤ}. Chứng minh rằng A ⊂ B.
Lời giải.
Ta cần chứng minh mọi phần tử của A đều thuộc B.
Giả sử x ∈ A, x = 8k + 3.
Khi đó ta có thể viết x = 8k + 2 + 1 = 2(4k + 1) + 1.
Đặt l = 4k + 1, x được viết thành x = 2l + 1. Vậy x ∈ B.
Câu 13. Tìm tất cả các tập con của mỗi tập hợp sau:
a) A = {1; 2}.
b) B = {a; b; c}.
Lời giải.
a) Các tập hợp con của tập hợp A = {1; 2} là: ∅; {1}; {2}; {1; 2}.
b) Các tập hợp con của tập hợp B = {a; b; c} là: ∅; {a}; {b}; {c}; {a; b}; {a; c}; {b; c}; và {a; b; c}.
Câu 14. Cho các tập hợp sau:
A = {2; 3; 5};
B = {−4; 0; 2; 3; 5; 6; 8};
C = {x ∈ ℝ | x2 − 7x + 10 = 0}.
Hãy xác định xem tập nào là tập con của tập còn lại.
Lời giải.
Ta có: x2 − 7x + 10 = 0 ⇔ x = 2 ∨ x = 5
Vậy C ⊂ A ⊂ B.
Câu 15. Cho hai tập hợp sau:
A = {x ∈ ℝ | (x − 1)(x − 2)(x − 4) = 0};
B = {n ∈ ℕ | n là một ước của 4}.
Hai tập hợp A và B, tập hợp nào là tập con của tập còn lại? Hai tập hợp A và B có bằng nhau không?
Lời giải.
Ta có: A = {1; 2; 4}; B = {1; 2; 4}.
Ta thấy A ⊂ B; B ⊂ A, nên A = B
Câu 16. Cho các tập hợp:
A ={x ∈ ℝ | x2 + x − 6 = 0 hoặc 3x2 − 10x + 8 = 0}
B ={x ∈ ℝ | x2 – x − 2 = 0 và 2x2 − 7x + 6 = 0}.
a) Viết tập hợp A, B bằng cách liệt kê các phần tử của nó.
b) Tìm tất cả các tập X sao cho B ⊂ X và X ⊂
Lời giải.
Ta giải các phương trình:
a)
b) X là những tập hợp sau:
Câu 17. Tìm tập hợp
a) Có đúng một tập con.
b) Có đúng hai tập con.
Lời giải.
a) Tâp hợp có đúng một tập con là ∅.
b) Tập A = {a}. A có đúng hai tập con là A và ∅.
Câu 18. Cho hai tập hợp sau:
A = {x ∈ ℤ | x là bội của 3 và 4};
B = {x ∈ ℤ | x là bội của 12}.
Chứng minh rằng A = B.
Lời giải.
Giả sử x ∈ B, khi đó x chia hết cho 12, suy ra x chia hết cho 3 và x chia hết cho 4, suy ra x ∈ A, do đó B ⊂ A.
Giả sử x ∈ A, khi đó x chia hết cho 3 và x chia hết cho 4, mà 3 và 4 nguyên tố cùng nhau nên suy ra x chia hết cho 3⋅4, hay x chia hết cho 12, suy ra x ∈ B, do đó A ⊂ B.
Vậy A = B.
Câu 19. Gọi A là tập hợp các tam giác đều, B là tập hợp các tam giác có góc 60°, C là tập hợp các tam giác cân, D là tập hợp các tam giác vuông có góc 30°. Hãy nêu mối quan hệ giữa các tập hợp trên.
Lời giải.
Vì tam giác đều là tam giác có ba góc bằng 60° nên A ⊂ B.
Tam giác đều cũng là tam giác cân nên A ⊂ C.
Tam giác vuông có góc 30° thì góc còn lại là 60° nên D ⊂ B.
Câu 20. Cho A = {3k + 2 | k ∈ ℤ}; B = {6k + 2 | k ∈ ℤ}
a) Chứng minh rằng 2 ∈ A,7 ∉ Số 18 có thuộc tập A không?
b) Chứng minh rằng B ⊂
Lời giải.
a) Ta có: 2 = 2 + 3⋅0 ⇒ 2 ∈
Ta thấy x ∈ B thì x có dạng x = 6k + 2 chia hết cho 2 nên −7 ∉ B.
Giả sử số 18 ∈ A ⇒ 18 = 3k + 2 ⇒ k = (vô lý) vì k ∈ ℤ.
Vậy 18 ∉ A.
b) Xét x ∈ Ta có x = 2 + 6k với k ∈ ℤ.
Suy ra x = 2 + 3(2k). Do 2k ∈ ℤ nên x ∈ A.
Vậy B ⊂ A.
Câu 21. Tìm tất cả các tập con của tập hợp B = {a, b, 2, 5}.
Lời giải.
Vì tập hợp B có 4 phần tử nên tập B có 24 = 16 tập con.
– 0 phần tử: ∅.
– 1 phần tử: {a}, {b}, {2}, {5}.
– 2 phần tử: {a, b}, {a, 2}, {a, 5}, {b, 2}, {b, 5}, {2; 5}.
– 3 phần tử: {a, b, 2}, {a, b, 5}, {a, 5, 2}, {5, b, 2}.
– 4 phần tử: {a, b, 2, 5}
Câu 22. Tìm tất cả các tập con có 3 phần tử của tập hợp D = {2, 3, 4, 6, 7}.
Lời giải.
{2, 3, 4}, {2, 3, 6}, {2, 3, 7},{2, 4, 6}, {2, 4, 7}, {2, 6, 7}, {3, 4, 6}, {3, 4, 7},{3, 6, 7}, {4, 6, 7}.
Câu 23. Xác định tập hợp X biết {a} ⊂ X ⊂ {a, 3, 4}.
Lời giải.
Tập hợp X có thể là {a},{a, 3},{a, 4},{a, 3, 4}.
Câu 24. Xác định tập hợp X biết {a, 9} ⊂ X ⊂ {a, b, 7, 8, 9} và tập hợp X có 3 phần tử.
Lời giải.
Tập hợp X có thể là {a, 9, b},{a, 7, 9,},{a, 8, 9}.
Câu 25. Cho hai tập hợp A = {x ∈ ℤ | x chia hết cho 2 và 5} và B = {x ∈ ℤ | x có chữ số tận cùng bằng 0}. Chứng minh rằng A = B.
Lời giải.
Trước hết, ta cần chứng minh A ⊂ B.
Thật vậy, với x ∈ A bất kì, ta luôn có x chia hết cho 2 và x chia hết cho 5.
Vì 2, 5 là hai số nguyên tố cùng nhau nên x chia hết cho 10. Suy ra, x ∈ B.
Mặt khác, với phần tử x ∈ B bất kì, vì x có chữ số tận cùng là 0 nên x chia hết cho 2 và 5. Suy ra, x ∈ A.
Do đó, B ⊂ A.
Câu 26. Tìm giá trị các tham số m và n sao cho {x ∈ ℝ | x3 − mx2 + nx − 1 = 0} = {1; 2}.
Lời giải.
Đặt A = {x ∈ ℝ | x3 − mx2 + nx − 1 = 0} và B = {1; 2}.
Vì 1 ∈ A nên –m + n = 0.
Vì 2 ∈ A nên −4m + 2n = −7.
Từ đây, ta có hệ phương trình m = n = .
Ngược lại, với m = n = , ta có:
Câu 27. Cho A là tập hợp tất cả các tứ giác lồi, B là tập hợp tất cả các hình thang, C là tập hợp tất cả các hình bình hành, D là tập hợp tất cả các hình chữ nhật. Xác định mối quan hệ giữa các tập hợp đã cho.
Lời giải.
D ⊂ C ⊂ B ⊂ A.
Câu 28. Cho các tập hợp
A = {1; 2}; B = {x ∈ ℝ | x2 − 3x + 2 = 0}; C = {x ∈ ℕ | x < 3}.
Hãy xác định mối quan hệ giữa các tập hợp trên.
Lời giải.
Ta có: B = {1; 2}; C = {0; 1; 2}
Vậy A ⊂ C; B ⊂ C; A = B.
Câu 29. Cho A là tập hợp các số nguyên chia cho 3 dư 2, B là tập hợp các số nguyên chia cho 6 dư 2 hoặc dư 5. Chứng minh rằng A = B.
Lời giải.
Ta chứng minh mọi phần tử của A đều là phần tử của B và ngược lại.
Trước hết ta thấy rằng một số chia hết cho 3 thì chia cho 6 dư 0 hoặc dư 3 nên một số chia cho 3 dư 2 thì chia cho 6 dư 2 hoặc dư 5.
Tức là nếu x ∈ A, x = 3k + 2 thì x có thể viết thành x = 6l + 2 hoặc x = 6l + 5 hay x ∈ B.
Ngược lại, x ∈ B xét hai trường hợp:
– Nếu x = 6k + 2 = 3(2k) + 2. Đặt l = 2k ⇒ x = 3l + 2 ⇒ x ∈ A
– Nếu x = 6k + 5 = 3(2k + 1) + 2. Đặt l = 2k + 1 ⇒ x = 3l + 2 ⇒ x ∈ A
Vậy A ⊂ B và B ⊂ A nên A = B (điều phải chứng minh).
Bạn đang xem bài viết Lý thuyết và bài tập về các tập hợp số xem thêm các bài viết khác về chủ đề Toán lớp 10. Chúc bạn 1 ngày vui vẻ!