Bạn đang xem bài viết 3 dạng giới hạn hàm số thường gặp. Hi vọng sẽ là đáp án bạn ưng ý. Cùng theo dõi nhé!
Bài viết chia sẽ các công thức tính giới hạn hàm số theo từng trường hợp như giới hạn cơ bản, giới hạn vô cực kèm theo đó là những bài tập vận dụng phù hợp. Mong rằng, bạn đọc sẽ nắm vững bài học hôm nay một cách nhanh chóng nhất.
Lý thuyết giới hạn hàm số
1. Giới hạn hữu hạn của hàm số tại một điểm
1.1. Khái niệm giới hạn hàm số tại một điểm
Cho khoảng ???? chứa điểm x0 và hàm số y = f(x) xác định trên ???? hoặc trên ????\ {x0}.
Ta nói hàm số y = f(x) có giới hạn là số L khi x dần tới x0 nếu với dãy số (xn) bất kỳ, xn ∊ K \ {x0} và xn → x0, ta có lim f(xn) = L.
Kí hiệu hay f(x) → L khi x → x0.
1.2. Ví dụ giới hạn hàm số tại một điểm
Ví dụ 1. Cho hàm số . Chứng minh rằng
.
Lời giải
Tập xác định: D = ℝ \ {–2}.
Giả sử (xn) là một dãy số bất kỳ, thỏa mãn xn ≠ –2 và xn → –2 khi n → +∞.
Ta có:
Do đó:
Chú ý: , với c là hằng số.
2. Giới hạn hữu hạn
2.1. Định lí giới hạn hữu hạn
a) Giả sử và
. Khi đó
+)
+)
+)
+)
b) Nếu f(x) ≥ 0 và , thì
L ≥ 0 và .
(Dấu của f(x) được xét trên khoảng đang tìm giới hạn, với x ≠ x0).
2.2. Ví dụ giới hạn hữu hạn
Ví dụ 1. Tính .
Lời giải
3. Giới hạn một bên
3.1. Định nghĩa giới hạn một bên
+) Cho hàm số y = f(x) xác định trên khoảng (x0; b).
Số L được gọi là giới hạn bên phải của hàm số y = f(x) khi x → x0 nếu với dãy số (xn) bất kì, x0 < xn < b và xn → x0, ta có f(xn) → L.
Kí hiệu:
+) Cho hàm số y = f(x) xác định trên khoảng (a; x0).
Số L được gọi là giới hạn bên trái của hàm số y = f(x) khi x → x0 nếu với dãy số (xn) bất kì, a < xn < x0 và xn → x0, ta có f(xn) → L.
Kí hiệu:
3.2. Định lí giới hạn một bên
khi và chỉ khi
.
3.3. Ví dụ gới hạn một bên
Ví dụ 1. Cho hàm số .
Tìm , và
(nếu có).
Lời giải
Ta có
Theo định lí 2, không tồn tại.
4. Giới hạn hữu hạn của hàm số tại vô cực
4.1. Định nghĩa giới hạn hữu hạn tại vô cực
a) Cho hàm số y = f(x) xác định trên khoảng (a; +∞).
Ta nói hàm số y = f(x) có giới hạn là số L khi x → +∞ nếu với dãy số (xn) bất kì, xn > a và xn → +∞, ta có f(xn) → L.
Kí hiệu: hay f(x) → L khi x → +∞.
b) Cho hàm số y = f(x) xác định trên khoảng (−∞; a).
Ta nói hàm số y = f(x) có giới hạn là số L khi x → −∞ nếu với dãy số (xn) bất kì, xn < a và xn → −∞, ta có f(xn) → L.
Kí hiệu: hay f(x) → L khi x → −∞.
4.2. Ví dụ về giới hạn hữu hạn tại vô cực
Ví dụ 1. Cho hàm số . Tìm
và
.
Lời giải
Hàm số đã cho xác định trên (−∞; 1) và trên (1; +∞).
Giả sử (xn) là một dãy số bất kỳ, thỏa mãn xn < 1 và xn → −∞.
Ta có:
Vậy
Giả sử (xn) là một dãy số bất kỳ, thỏa mãn xn > 1 và xn → +∞.
Ta có:
Vậy
Chú ý:
+) Với c, k là các hằng số và k nguyên dương, ta luôn có:
+) Định lí 1 về giới hạn hữu hạn của hàm số khi x → x0 còn đúng khi x → +∞ hoặc x → −∞.
Ví dụ 2. Tìm
Lời giải
5. Giới hạn vô cực của hàm số
5.1. Giới hạn vô cực của hàm số
Cho hàm số y = f(x) xác định trên khoảng (a; +∞).
Ta nói hàm số y = f(x) có giới hạn là −∞ khi x → +∞ nếu với dãy số (xn) bất kì, xn > a và xn → +∞, ta có f(xn) → −∞.
Kí hiệu: hay f(x) → −∞ khi x → +∞.
Nhận xét
Một vài giới hạn đặc biệt
+) với k nguyên dương.
+) nếu k là số lẻ.
+) nếu k là số chẵn.
Một vài quy tắc về giới hạn vô cực
Quy tắc tìm giới hạn của tích f(x).g(x)

Quy tắc tìm giới hạn của thương 

Các quy tắc trên vẫn đúng cho các trường hợp:
5.2. Ví dụ giới hạn vô cực của hàm số
Ví dụ 1. Tìm .
Lời giải
Ta có:
Vì và
.
Ví dụ 2: Tính .
Ta có: , vì
Dạng 1
Giới hạn của hàm số dạng vô định 0/0
1.1. Phương pháp giải
+) Biểu thức có dạng trong đó f(x), g(x) là các đa thức và f(x0) = g(x0) = 0.
Khử dạng vô định bằng cách phân tích cả tử và mẫu thành nhân tử với nhân tử chung là x – x0.
Giả sử f(x) = (x – x0). f1(x) và g(x) = (x – x0). g1(x). Khi đó:
=
Nếu giới hạn vẫn ở dạng vô định
thì ta lặp lại quá trình khử đến khi không còn dạng vô định.
Việc phân tích thành nhân tử ở trên được thực hiện bằng phương pháp chia Horner.
+) Biểu thức có dạng trong đó f(x), g(x) là các biểu thức có chứa căn thức và f(x0) = g(x0) = 0.
Khử dạng vô định bằng cách nhân cả tử và mẫu với biểu thức liên hợp tương ứng của biểu thức chứa căn thức để trục các nhân tử x – x0 ra khỏi các căn thức, nhằm khử các thành phần có giới hạn bằng 0. Lưu ý có thể nhân liên hợp một hay nhiều lần để khử dạng vô định.
Chú ý: Các hằng đẳng thức
A2 – B2 = (A – B).(A + B)
A3 – B3 = (A – B).(A2 + AB + B2)
A3 + B3 = (A + B).(A2 – AB + B2)
1.2. Bài tập vận dụng
Câu 1. Tính các giới hạn sau:
a)
b)
c)
d)
Lời giải
a)
b)
c)
d)
Câu 2. Tính giới hạn .
Lời giải
Câu 3. Tính giới hạn .
Lời giải
Câu 4. Tính giới hạn .
Lời giải
Câu 5. Tính giới hạn .
Lời giải
Câu 6. Tính giới hạn với n là số nguyên dương.
Lời giải
Đặt t = 1 + x. Suy ra x = t – 1. Khi x → 0 thì t → 1.
Do đó:
Câu 7. Tính giới hạn với a ≠ 0.
Lời giải
Câu 8. Tính giới hạn với a ≠ 0.
Lời giải
Câu 9. Tính giới hạn với a ≠ 0, n là số nguyên và n ≥ 2.
Lời giải
Đặt
Suy ra
Khi x → 0 thì t → 1. Do đó:
Chú ý: Các giới hạn với n ∈ ℕ; và
với a ≠ 0, n là số nguyên và n ≥ 2 được gọi là các “giới hạn cơ bản”.
Câu 10. Tính giới hạn
.
Lời giải
Câu 11. Tính các giới hạn sau:
a)
b)
c)
d)
Lời giải
a)
b)
c)
d)
Câu 12. Tính giới hạn .
Lời giải
Câu 13. Tính giới hạn
.
Lời giải
Câu 14. Tính giới hạn .
Lời giải
Câu 15. Tính giới hạn .
Lời giải
Câu 16. Tính giới hạn
.
Lời giải
Ta có:
Với n là số tự nhiên không bé hơn 2, ta sẽ chứng minh . Thật vậy, đặt
và khi x → 1 thì t → 1.
Khi đó ta có:
Từ đó suy ra:
Câu 17. Tính giới hạn .
Lời giải
Câu 18. Tính các giới hạn sau:
a)
b)
c)
d)
Lời giải
a)
b)
c)
d)
Câu 19. Tính các giới hạn sau:
a)
b)
c)
d)
Lời giải
a)
b)
c)
d)
Câu 20. Tính giới hạn .
Lời giải
Câu 21. Tính giới hạn .
Lời giải
Câu 22. Tính giới hạn .
Lời giải
Câu 23. Tính giới hạn .
Lời giải
Câu 24. Tính giới hạn .
Lời giải
Câu 25. Tính giới hạn .
Lời giải
Câu 26. Tính giới hạn .
Lời giải
Câu 27. Tính giới hạn
.
Lời giải
Câu 28. Tính giới hạn .
Lời giải
Câu 29. Tính giới hạn .
Lời giải
Câu 30. Tính giới hạn .
Lời giải
Ta có:
Do đó:
Câu 31. Tính giới hạn .
Lời giải
Ta có:
Do đó:
Câu 32. Tính giới hạn .
Lời giải
Ta có:
Do đó:
Câu 33. Tính giới hạn
.
Lời giải
Ta có:
Do đó:
Câu 34. Tính giới hạn
.
Lời giải
Ta có:
Do đó:
Câu 35. Tính giới hạn
.
Lời giải
Ta có:
Do đó:
Câu 36. Tính giới hạn .
Lời giải
Câu 37. Tính giới hạn .
Lời giải
Câu 38. Tính giới hạn .
Lời giải
Ta có:
Do đó:
Câu 39. Tính giới hạn
Lời giải
Ta có:
Do đó:
Câu 40. Tính giới hạn .
Lời giải
Ta có:
Do đó:
Câu 41. Tính giới hạn
.
Lời giải
Do đó:
Câu 42. Tính giới hạn .
Lời giải
Ta có:
Do đó:
Câu 43. Tính giới hạn .
Lời giải
Ta có:
Do đó:
Câu 44. Tính I + J, biết:
và
.
Lời giải
Ta có:
Vậy I + J = 4.
Câu 45. Tính giới hạn
.
Lời giải
Ta có:
Câu 46. Tính giới hạn .
Lời giải
Đặt , và khi x → 7 thì t → 2. Khi đó:
Câu 47. Tính giới hạn .
Lời giải
Ta có:
Câu 48. Tính giới hạn .
Lời giải
Ta có:
Câu 49. Tính giới hạn
Lời giải
Ta có:
Câu 50. Tính giới hạn .
Lời giải
Ta có:
Câu 51. Với α∙ β ≠ 0 và m, n là số nguyên dương. Tính giới hạn
Lời giải
Ta có:
Do đó:
Câu 52. Tính giới hạn với a ≠ 0 và α, β là các số nguyên dương.
Lời giải
Câu 53. Tính giới hạn với n là số nguyên dương.
Lời giải
Ta có:
Do đó:
Câu 54. Tính giới hạn
Lời giải
Ta có:
Do đó:
Câu 55. Tính giới hạn
.
Lời giải
Ta có:
Do đó:
Câu 56. Tính giới hạn .
Lời giải
Ta có:
Do đó:
Câu 57. Tính giới hạn .
Lời giải
Ta có:
Câu 58. Tính giới hạn .
Lời giải
Do đó:
Câu 59. Tính giới hạn
.
Lời giải
Nhận xét:
.
Khi đó:
Do đó:
Câu 60. Tính giới hạn
.
Lời giải
Ta có:
Do đó:
Dạng 2
Giới hạn vô định (∞/∞, ∞ – ∞, 0.∞)
2.1. Phương pháp giải
Loại 1:  với P(x), Q(x) là đa thức hoặc các hàm đại số
với P(x), Q(x) là đa thức hoặc các hàm đại số
Phương pháp: Gọi p = deg P(x), q = deg Q(x) và m = min (p, q).
+) Nếu p ≤ q thì tồn tại giới hạn.
+) Nếu p > q thì không tồn tại giới hạn.
Loại 2: Giới hạn ∞ − ∞
Phương pháp sử dụng các biểu thức liên hợp đưa về dạng .
Loại 3: Giới hạn 0∙∞
Phương pháp sử dụng các biểu thức liên hợp đưa về dạng .
2.2. Bài tập vận dụng
Câu 1. Tính
Lời giải
Ta có:
Câu 2. Tính
Lời giải
Ta có:
Câu 3. Tìm giới hạn
Lời giải
Ta có:
Câu 4. Tìm giới hạn
Lời giải
Ta có:
Câu 5. Tìm giới hạn
Lời giải
Ta có:
Câu 6. Tính
Lời giải
Ta có:
Câu 7. Tính
Lời giải
Ta có:
Câu 8. Tính
Lời giải
Ta có:
Câu 9. Tính
Lời giải
Ta có:
Câu 10. Tính
Lời giải
Ta có:
Suy ra:
Câu 11. Tính
Lời giải
Ta có
Câu 12. Tính giới hạn
Lời giải
Ta có:
Câu 13. Tính giới hạn
Lời giải
Ta có:
Câu 14. Tính giới hạn
Lời giải
Ta có:
Câu 15. Tính giới hạn
Lời giải
Ta có
Câu 16. Tính giới hạn
Lời giải
Câu 17. Tính giới hạn
Lời giải
Ta có
h257
= 0
Câu 18. Tính giới hạn
Lời giải
Ta có:
Câu 19. Tìm giới hạn
Lời giải
Ta có:
Dạng 3
Tính giới hạn hàm đa thức, hàm phân thức và giới hạn một bên.
3.1. Phương pháp giải
+) Nếu và
thì:
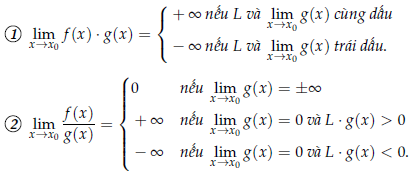
+)
3.2. Bài tập vận dụng
Câu 1. Tính giới hạn của các hàm số sau:
a)
b)
c)
d)
e)
f)
Lời giải
a)
b)
Do:
Và
Nên: = +∞
c) = −∞
d) = −∞
e) = +∞
f) = +∞
Câu 2. Tính giới hạn của các hàm số sau:
a)
b)
c)
d)
Lời giải
a) = 0
Vì:
b) Ta có:
và x – 3 > 0, ∀x > 3.
Do đó: = −∞.
c) = −∞.
d) Ta có:
Câu 3. Tính giới hạn một bên của các hàm số sau tại điểm được chỉ ra:
a) tại x = 1;
b) tại x = 2.
Lời giải
a) Ta có:
Và:
b) Ta có:
Và:
Từ đó suy ra:
Câu 4. Tính các giới hạn sau:
a)
b)
c)
d)
Lời giải
a)
b)
c)
d)
Câu 5. Tính các giới hạn sau:
a)
b)
c)
d)
Lời giải
a) Ta có:
và x + 1 < 0, ∀x < –1
Do đó I1 = −∞.
b)
c)
d)
Câu 6. Tính giới hạn
Lời giải
Xét các giới hạn một bên:
+)
+) .
Từ đó suy ra không tồn tại.
Câu 7. Cho hàm số
.
Xác định các giá trị của tham số m để f(x) có giới hạn tại điểm x = 1.
Lời giải
Ta có
Để tồn tại thì điều kiện cần và đủ
Câu 8. Tính các giới hạn:
a)
b)
c)
d)
Lời giải
a) I1 = +∞
b)
c)
d) I4 = 4
Câu 9. Tính các giới hạn sau:
a)
b)
Lời giải
a)
b)
Câu 10. Cho hàm số
.
Biết rằng a, b là các số thực thỏa mãn hàm số f(x) có giới hạn tại x = 1.
a) Tìm mối quan hệ giữa a và b.
b) Tìm giá trị nhỏ nhất của biểu thức P = a2 + b2.
Lời giải
a) Ta có:
Hàm số f(x) có giới hạn tại x = 1 khi và chỉ khi –3a = 2b + 1.
b) Từ câu a) ta có:
Đẳng thức có được khi và chỉ khi và
.
Vậy:
Câu 11. Tính các giới hạn sau:
a)
b)
c)
d)
Lời giải
a) Ta có:
b) Ta có:
2x4 + 9x3 + 11x2 – 4 = (x + 2)2.(2x2 + x – 1)
Suy ra:
c)
d) Ta có: x + x2 + ⋯+ x2018 – 2018
= (x – 1) + (x2 – 1) + ⋯ + (x2018 – 1)
= (x – 1).[1 + (1 + x) + ⋯ + (1 + x + x2 + ⋯ + x2017)].
Do đó:
Câu 12. Tìm các giá trị của a, b sao cho:
.
Lời giải
Nếu a ≤ 0 thì:
Do đó, ta chỉ xét với a > 0. Khi đó, ta có:
Suy ra 1 – a2 = 0 ⇔ a = ±1.
+) Với a = 1 thì
khi
+) Với a = –1 tương tự ta tìm được .
Câu 13. Tính các giới hạn sau:
a)
b)
c)
d)
Lời giải
a) Ta có:
b) Ta có:
c) Ta có:
d) Ta có:
Câu 14. Tính các giới hạn sau:
a)
b)
c)
d)
Lời giải
a)
b)
c)
d) Ta có:
Vậy:
Bạn đang xem bài viết 3 dạng giới hạn hàm số thường gặp xem thêm các bài viết khác về chủ đề Toán lớp 11. Chúc bạn 1 ngày vui vẻ!