Bạn đang xem bài viết Phương trình tiếp tuyến | Phân dạng & cách giải chi tiết (Có tài liệu). Hi vọng sẽ là đáp án bạn ưng ý. Cùng theo dõi nhé!
Tìm hiểu cách viết phương trình tiếp tuyến của đồ thị hàm số f(x) tại điểm, khi biết hệ số góc hoặc dựa vào các dữ liệu đường tiệm cận. Bài viết sẽ giới thiệu đến bạn đọc 5 dạng bài tập đặc trưng nhất và thường gặp nhất. Tuy nhiên trước tiên đi đến phần bài tập thì việc nhắc lại lý thuyết là điều kiện tiên quyết.
Tiếp tuyến là gì?
Tiếp tuyến của một đường cong tại một điểm bất kỳ thuộc đường cong là đường thẳng chỉ “chạm” vào đường cong tại điểm đó. Nhà toán học Leibniz định nghĩa tiếp tuyến như một đường thẳng nối một cặp điểm gần nhau vô hạn trên đường cong.
Nói chính xác hơn, một đường thẳng là tiếp tuyến của một đường cong y = f(x) tại điểm x = c trên đường cong nếu như đường thẳng đó đi qua điểm (c, f(c)) trên đường cong và có độ dốc f’(c) với f’ là đạo hàm của hàm số f.
Khi tiếp tuyến đi qua giao điểm của tiếp tuyến và đường cong trên, giao điểm đó gọi là tiếp điểm. Khái niệm tiếp tuyến là một trong những khái niệm cơ bản nhất trong hình học vi phân và được tổng quát hóa một cách rộng rãi. [1]WikiPedia, Tiếp Tuyến, 7/01/2022
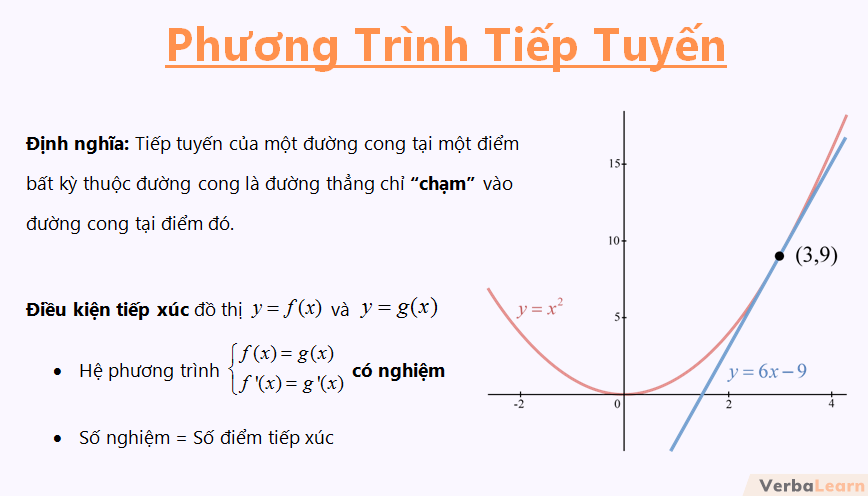Tiếp tuyến của một đường cong tại một điểm bất kỳ thuộc đường cong là đường thẳng chỉ “chạm” vào đường cong tại điểm đó.
Lý thuyết về tiếp tuyến của hàm số
1. Định nghĩa về tiếp tuyến, tiếp điểm
Cho hai hàm số f(x) và g(x) có đạo hàm tại điểm x0. Ta nói rằng hai đường cong (C): y = f(x) và (C’): y = g(x) tiếp xúc với nhau tại điểm M (x0; y0) nếu M là một tiếp điểm chung của chúng. → (C) và (C’) có tiếp tuyến chung tại M.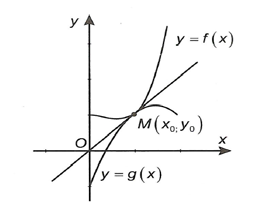
(C) và (C’) có tiếp tuyến chung tại M.
2. Điều kiện tiếp xúc
Hai đường cong (C): y = f(x) và (C’): y = g(x) tiếp xúc với nhau ⇔ Hệ phương trình 
có nghiệm.
Khi đó: Nghiệm của hệ phương trình là hoành độ tiếp điểm của hai đường cong đó.
Phân dạng và phương pháp giải bài tập tiếp tuyến
Dạng 1: Sự tiếp xúc của hai đường cong
Phương pháp giải
Cho hai đường cong (C): y = f(x) và (C’): y = g(x). Điều kiện để hai đường cong tiếp xúc nhau là hệ phương trình có nghiệm.
Nghiệm x = x0 của hệ trên là hoành độ của tiếp điểm của hai đường cong đã cho.
Hệ trên có bao nhiêu nghiệm thì hai đường cong (C) và (C’) tiếp xúc với nhau tại bấy nhiêu điểm.
Bài tập vận dụng
[ads]
Bài tập 1: Đồ thị hàm số y = x3 + x + 1 tiếp xúc với đường thẳng nào dưới đây?
A. y = x + 1
B. y = -2x + 1
C. y = -x + 1
D. y = 2x + 1
Hướng dẫn giải
Chọn A.
Áp dụng điều kiện tiếp xúc của hai đường cong (C): y = f(x) và (C’): y = g(x) là hệ phương trình có nghiệm.
Ta có y’ = 3x2 + 1 > 0, ∀ x ∊ ℝ nên các phương án B, C bị loại.
Xét phương án A, y = x + 1. Ta có hệ 
.
Vậy đường thẳng y = x + 1 tiếp xúc với đồ thị hàm số đã cho.
Bài tập 2: Tập hợp tất cả các giá trị thực của tham số m để đường thẳng y = -2x + m tiếp xúc với đồ thị hàm số 
.
A. {7; -1}
B. {-1}
C. {6}
D. {6; -1}
Hướng dẫn giải
Chọn A.
Đường thẳng y = -2x + m tiếp xúc với đồ thị hàm số H3 khi và chỉ khi hệ phương trình sau có nghiệm
Vậy m ∊ {-1; 7} thì đường thẳng d tiếp xúc với (C).
Bài tập 3: Gọi S là tập hợp tất cả các giá trị thực của tham số m dể đồ thị (Cm) của hàm số y = x3 – 4mx2 + 7mx – 3m tiếp xúc với parabol (P): y = x2 – x + 1. Tổng giá trị các phần tử của S bằng
A. 
B. 
C. 
D. -4
Hướng dẫn giải
Chọn A.
Để (Cm) tiếp xúc với (P) thì hệ phương trình sau có nghiệm:
⇔ 
Giải (1), ta có (1) ⇔ (x – 1) (x2 – 4mx + 3m + 1) = 0
⇔ .
Với x = 1 thay vào (2) được m = 2
Xét hệ 
.
Nếu 
thì (4) vô nghiệm.
Nếu 
thì (4) ⇔ 
.
Thay vào (3) ta được 
.
⇔ 
(thỏa mãn điều kiện).
Vậy 
nên tổng các phần tử trong S bằng .
Bài tập 4: Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số 
tiếp xúc với đường thẳng y = 1. Tổng giá trị các phần tử của S bằng
A. 10
B. 
C. 
D. 
Hướng dẫn giải
Chọn B.
Xét hệ phương trình 
Giải phương trình (2) ta được 
.
Với x = m, thay vào (1) ta được 
.
Với x = 2, thay vào (1), ta được 
.
Vậy tập hợp các giá trị của tham số thực để dồ thị hàm số đã cho tiếp xúc với đường thẳng y – 1 là 
nên tổng các phần tử trong S bằng .
Bài tập 5: Biết đồ thị hàm số (C): y = x3 + ax2 + bx + c (a, b, c ∊ ℝ), tiếp xúc với trục hoành tại gốc tọa độ và cắt đường thẳng x = 1 tại điểm có tung độ bằng 3. Tổng a + 2b + 3c bằng
A. 4
B. 2
C. 6
D. 3
Hướng dẫn giải
Chọn B.
Vì (C) tiếp xúc với Ox tại gốc tọa độ nên x = 0 là nghiệm của hệ phương trình
Mặt khác (C) đi qua điểm A (1; 3) nên a + b + c + 1 = 3 ⇒ a = 2.
Vậy a + 2b + 3c = 2.
Bài tập 6: Họ parabol (Pm): y = mx2 – 2 (m – 3) x + m – 2 (m ≠ 0) luôn tiếp xúc với đường thẳng d cố định khi m thay đổi. Đường thẳng d đi qua điểm nào dưới dây?
A. A(1; -8)
B. B(0; -2)
C. C(0; 2)
D. D(1; 8)
Hướng dẫn giải
Chọn B.
Ta có: y = mx2 – 2(m – 3) x + m – 2 = m(x2 – 2x + 1) + 6x – 2
⇔ y = m(x – 1)2 + 6x – 2.
Xét đường thẳng d: y = 6x – 2 thì hệ phương trình
luôn có nghiệm x = 1 với mọi x ≠ 0.
Vậy (Pm) luôn tiếp xúc với đường thẳng d: y = 6x – 2.
Đường thẳng d đi qua điểm B (0; -2).
Nhận xét: Nếu có thể viết lại hàm số (Pm) theo dạng y = (ax + b)2 + cx + d thì (Pm) luôn tiếp xúc với đường thẳng y = cx + d.
Dạng 2: Lập phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm M (x0; y0)
Phương pháp giải
Thực hiện theo các bước sau
- Bước 1: Tính y’ = f’(x) và f’(x0).
- Bước 2: Suy ra phương trình tiếp tuyến cần tìm là y = f’(x0) (x – x0) + y0
- Bước 3: Thực hiện các yêu cầu còn lại của bài toán. Kết luận.
Chú ý:
- Nếu bài toán chỉ cho x0 thì ta cần tìm y0 = f(x0) và f’(x0).
- Nếu bài toán chỉ cho y0 thì ta cần tìm x0 bằng cách giải phương trình f(x) = y0.
- Giá trị f’(x0) là hệ số góc của tiếp tuyến của đồ thị hàm số y = f(x) tại điểm M (x0; y0).
Bài tập vận dụng
Bài tập 1: Gọi M là điểm thuộc đồ thị hàm số (C): 
có tung độ bằng 5. Tiếp tuyến của đồ thị (C) tại M cắt các trục Ox, Oy lần lượt tại A, B. Diện tích tam giác OAB bằng
A. 
(đvdt)
B. 
(đvdt)
C. 
(đvdt)
D. 
(đvdt)
Hướng dẫn giải
Chọn C.
Ta có M (2; 5) ∊ (C); 
; y’ (2) = -3.
Phương trình tiếp tuyến tại M (2; 5) là d: y = -3x + 11.
Khi đó d cắt Ox, Oy tại 
và B (0; 11) ⇒ 
; OB = 11.
Vậy 
(đvdt)
Bài tập 2: Cho hàm số 
. Biết rằng a và b là các giá trị thỏa mãn tiếp tuyến của đồ thị hàm số tại điểm A (1; -2) song song với đường thẳng d: 3x + y – 4 = 0. Khi đó giá trị của a – 3b bằng
A. 5
B. 4
C. -1
D. -2
Hướng dẫn giải
Chọn D.
Ta có 
Do tiếp tuyến song song với đường thẳng d: 3x + y – 4 = 0 ⇔ y = -3x + 4 nên 
.
Mặt khác A (1; -2) thuộc đồ thị hàm số 
.
Khi đó ta có hệ 
.
Với a = 2 ⇒ b = -1 ⇒ ab = -2 (loại)
Với a = 1 ⇒ b = 1 (thỏa mãn điều kiện).
Khi đó ta có hàm số 
.
nên phương trình tiếp tuyến là y = -3x + 1 song song với đường thẳng y = -3x + 4
Vậy a – 3b = -2.
Bài tập 3: Trong tất cả các đường thẳng tiếp xúc với đồ thị hàm số y = -x3 – 3x2 + 3x + 1 thì đường thẳng d có hệ số góc lớn nhất. Phương trình đường thẳng d là
A. y = 6x + 2
B. y = 2x + 2
C. y = 1
D. y = 3x + 1
Hướng dẫn giải
Chọn A.
Ta có y’ = -3x2 – 6x + 3
Gọi M (x0; y0) thuộc đồ thị hàm số. Khi đó hệ số góc của tiếp tuyến tại M (x0; y0) là 
.
⇒ kmax = 6 ⇔ x0 = -1 hay M (-1; -4).
Phương trình đường thẳng d là y = 6 (x + 1) – 4 ⇔ y = 6x + 2.
Nhận xét: Đối với hàm số bậc ba y =ax3 + bx2 + cx + d thì tiếp tuyến có hệ số góc lớn nhất (nhỏ nhất) là tiếp tuyến tại điểm uốn của đồ thị U (x0; f(x0)), với x0 là nghiệm của phương trình y’’ = 0.
– Nếu a > 0 thì hệ số góc k = f’(x0) là nhỏ nhất.
– Nếu a < 0 thì hệ số góc k = f’(x0) là lớn nhất.
Bài tập 4: Cho hàm số y = x3 – 2x2 + (m – 1) x + 2m có đồ thị (Cm). Giá trị thực của tham số m để tiếp tuyến của đồ thị (Cm) tại điểm có hoành độ x = 1 song song với đường thẳng y = 3x + 10 là
A. m = 2
B. m = 4
C. m = 0
D. không tồn tại m
Hướng dẫn giải
Chọn D.
Có y’ = 3x2 – 4x + m – 1 ⇒ y’ (1) = m – 2.
Tiếp tuyến của (Cm) tại điểm có hoành độ x = 1 có phương trình là
y = (m – 2) (x – 1) + 3m – 2 ⇔ y = (m – 2) x + 2m
Do tiếp tuyến song song với đường thẳng y = 3x + 10 nên 
(vô lí)
Vậy không tồn tại m thỏa mãn yêu cầu bài toán.
Bài tập 5: Cho hàm số f(x) = x3 + mx2 + x + 1. Gọi k là hệ số góc tiếp tuyến của đồ thị hàm số tại M có hoành dộ x = 1. Tất cả các giá trị của tham số m để thỏa mãn k. f (-1) < 0 là
A. m ≤ -2
B. -2 < m < 1
C. m ≥ 2
D. m > 2
Hướng dẫn giải
Chọn B.
Ta có: f’(x) = 3x2 + 2mx + 1 ⇒ k = f’ (1) = 4 + 2m.
Do đó k. f (-1) = (4 + 2m) (m – 1)
Để k. f (-1) < 0 thì (4 + 2m) (m – 1) < 0 ⇔ -2 < m < 1.
Bài tập 6: Cho hàm số y = x3 + 3mx2 + (m + 1) x + 1, với m là tham số thực, có đồ thị (C). Biết rằng khi m = m0 thì tiếp tuyến với đồ thị (C) tại điểm có hoành độ x0 = -1 đi qua A (1; 3). Mệnh đề nào sau đây đúng?
A. -2 < m0 < -1
B. -1 < m0 < 0
C. 0 < m0 < 1
D. 1 < m0 < 2
Hướng dẫn giải
Chọn C.
Gọi B là tiếp điểm của tiếp tuyến đi qua A (1; 3) khi m = m0
Ta có y’ = 3x2 + 6mx + m + 1.
Với x0 = -1 thì y0 = 2m – 1 ⇒ B (-1; 2m – 1) và y’ (-1) = -5m + 4.
Tiếp tuyến tại B của (C) có phương trình là y = (-5m + 4) (x + 1) + 2m – 1.
Do tiếp tuyến đi qua A (1; 3) nên 2 (-5m + 4) + 2m – 1 = 3 ⇔ 
.
Vậy 
.
Bài tập 7: Cho hàm số 
có đồ thị (C). Gọi M là một điểm thuộc (C) có khoảng cách từ M đến trục hoành bằng hai lần khoảng cách từ M đến trục tung, M không trùng với gốc tọa độ O và có tọa độ nguyên. Phương trình tiếp tuyến của (C) tại M là
A. y = -8
B. y = -64
C. y = -12
D. y = -9
Hướng dẫn giải
Chọn A.
Giả sử 
là một điểm thuộc (C).
Do d (M; Ox) = 2d (M; Oy) nên 
.
Theo giả thiết thì M không trùng với gốc tọa độ O và có tọa độ nguyên nên a = 4 ⇒ M (4; -8).
Khi đó 
.
Phương trình tiếp tuyến cần tìm là y = -8.
Bài tập 8: Cho hàm số 
có đồ thị (C) và đường thẳng d: y = -2x + m – 1 (m là tham số thực). Gọi k1, k2 là hệ số góc tiếp tuyến của (C) tại giao điểm của d và (C). Tích k1. k2 bằng
A. 4
B. 
C. 2
D. 3
Hướng dẫn giải
Chọn A.
Tập xác định D = ℝ \ {-2}.
Ta có 
.
Xét phương trình hoành độ giao điểm của (C) và (d)
(Với x ≠ -2)
⇒ 
Để đường thẳng (d) cắt đồ thị hàm số (C) tại hai điểm thì phương trình (1) phải có hai nghiệm phân biệt khác -2.
⇔ 
Vậy (C) luôn cắt (d) tại hai điểm phân biệt A (x1; y1) và B (x2; y2), với x1, x2 là nghiệm của phương trình (1).
Theo định lý Vi-ét ta có 
Ta có 
= 
Bài tập 9: Cho hàm số y = x4 – 2mx2 + m có đồ thị (C) với m là tham số thực. Gọi A là điểm thuộc đồ thị (C) có hoành độ bằng 1. Giá trị của tham số thực m để tiếp tuyến ∆ của đồ thị (C) tại A cắt đường tròn (y): x2 + (y – 1) = 4 tạo thành một dây cung có độ dài nhỏ nhất là
A. 
B. 
C. 
D. 
Hướng dẫn giải
Đường tròn (y): x2 + (y – 1) = 4 có tâm I (0; 1), R = 2.
Ta có A (1; 1 – m); y’ = 4x3 – 4mx ⇒ y’ (1) = 4 – 4m.
Suy ra phương trình tiếp tuyến ∆: y = (4 – 4m) (x – 1) + 1 – m.
Dễ thấy ∆ luôn đi qua điểm cố định 
và điểm F nằm trong đường tròn (y).
Giả sử ∆ cắt (y) tại M, N, khi đó 
.
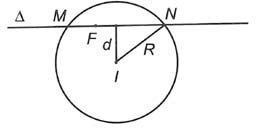
Do đó MN nhỏ nhất ⇔ d (I; ∆) lớn nhất ⇔ d (I; ∆) = IF ⇒ ∆ ⊥ IF.
Khi đó đường thẳng ∆ có 1 vectơ chỉ phương 
nên 
.
Dạng 3: Viết phương trình tiếp tuyến của đồ thị hàm số khi biết hệ số góc dựa vào các quan hệ song song, vuông góc, …
Phương pháp giải
Thực hiện theo một trong hai cách sau:
Cách 1
– Bước 1. Xác định hệ số góc k của tiếp tuyến dựa vào giả thiết bài toán.
– Bước 2. Giải phương trình f’(x) = k để tìm x = xo là hoành độ của tiếp điểm.
Tính yo = f(xo) ⇒ M (xo; y0).
Khi đó phương trình tiếp tuyến cần tìm là y = k (x – x0) + y0
Điểm M (x0; y0) là tiếp điểm của tiếp tuyến với đồ thị hàm số đã cho.
Cách 2
– Bước 1. Xác định hệ số góc k của tiếp tuyến dựa vào giả thiết bài toán.
– Bước 2. Vì tiếp tuyến có hệ số góc là k nên phương trình tiếp tuyến có dạng y = kx + b. Dựa vào điều kiện tiếp xúc của tiếp tuyến với (C) ta tìm giá trị của b.
Lưu ý
Phương trình f’(x) = k có bao nhiêu nghiệm thì có bấy nhiêu tiếp điểm.
Một số trường hợp xác định hệ số góc của đường thẳng thường gặp.
Cho hai đường thẳng
d1: y = k1x + b1; d2: y = k2x + b2.
Trường hợp 1: d1 ⊥ d2 ⇔ k1. k2 = -1.
Trường hợp 2: d1 // d2 ⇔ 
.
Trường hợp 3: Góc (d1; d2) = ∝ ⇒ 
.
Trường hợp đặc biệt
Nếu góc giữa d: y = kx + b với Ox bằng ⍺ (Oo < ∝ < 90o) thì |k| = tan ⍺.
Nếu đường thẳng d cắt Ox, Oy tại hai điểm A, B mà OB = m. OA thì |k| = tan ⍺ = 
.
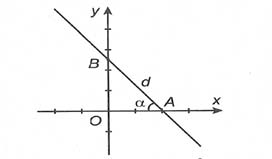
Trường hợp 4: Nếu đường thẳng d đi qua hai điểm A (x1; y1) và B (x2; y2) thì 
.
Bài tập vận dụng
[ads]
Bài tập 1: Phương trình tiếp tuyến của đồ thị hàm số y = x3 – 3x + 1 song song với trục Ox là
A. y = 3, y = -1
B. y = 3, y = -2
C. x = 3, x = -1
D. y = 2, y = -1
Hướng dẫn giải
Chọn A.
Do tiếp tuyến song song với trục Ox nên tiếp tuyến có tiếp điểm là các điểm cực trị và có phương trình y = y0 với y0 là giá trị cực trị của hàm số đã cho.
Ta có y’ = 3x2 – 3; y’ = 0 ⇔ x = ±1.
Do hàm số đã cho là hàm bậc ba nên các điểm cực trị là A (1; -1), và B (-1; 3).
Vậy phương trình các đường tiếp tuyến cần tìm là y = -1; y = 3.
Bài tập 2: Cho hàm số 
có đồ thị là (C). Phương trình tiếp tuyến của đồ thị (C) sao cho tiếp tuyến này cắt các trục Ox, Oy lần lượt tại các điểm A, B thỏa mãn OA = 4OB là
A. 
B. 
C. 
D. 
Hướng dẫn giải
Chọn C.
Do tiếp tuyến cắt Ox, Oy tại hai điểm A, B mà OA = 4OB.
Khi đó ∆OAB vuông tại O và ta có 
.
Ta có 
Xét phương trình 
(vô nghiệm).
Xét phương trình 
.
Với x = 3 thì 
. Phương trình tiếp tuyến là
.
Với x = -1 thì 
. Phương trình tiếp tuyến là
.
Bài tập 3: Đường thẳng nào dưới đây là tiếp tuyến của đồ thị hàm số 
chắn hai trục tọa độ một tam giác vuông cân?
A. y = x + 2
B. y = x – 2
C. y = -x + 2
D. 
Hướng dẫn giải
Chọn A.
Gọi A, B là giao điểm của tiếp tuyến lần lượt với Ox, Oy.
Vì ∆OAB vuông cân tại O nên OA = OB.
Do đó 
.
Ta có 
.
Xét phương trình 
(vô nghiệm).
Xét phương trình 
.
Với x = -1 thì y = 1. Phương trình tiếp tuyến là y = (x + 1) + 1 = x + 2.
Với x = -3 thì y = 3. Phương trình tiếp tuyến là y = (x + 3) + 3 = x + 6.
Bài tập 4: Cho hàm số 
có đồ thị là (Cm). Tất cả các giá trị thực của tham số m để trên đồ thị (Cm) tồn tại một điểm duy nhất có hoành độ âm mà tiếp tuyến tại đó vuông góc với đường thẳng d: x + 2y – 3 = 0 là
A. m < 12 hoặc 
B. m < 0 hoặc m > 1
C. m < 0 hoặc 
D. m < 0 hoặc
Hướng dẫn giải
Chọn D.
Ta có: d: x + 2y – 3 = 0 ⇔ nên hệ số góc của d là 
.
Do tiếp tuyến vuông góc với d nên hệ số góc của tiếp tuyến là k thì 
.
Gọi M (x0; y0) là tiếp điểm của tiếp tuyến với (Cm) thì x0 là nghệm của phương trình
y’ = k ⇔ mx2 + 2 (m – 1) x + 4 – 3m = 2.
⇔ mx2 + 2 (m – 1) x + 2 – 3m= 0 (*)
Theo bài toán thì ta phải tìm m để (*) có duy nhất một nghiệm âm.
Trường hợp 1: Nếu m = 0 thì (*) ⇔ –2x = -2 ⇔ x = 1 (loại).
Trường hợp 2: Nếu m ≠ 0. Ta thấy phương trình (*) có hai nghiệm x = 1 và 
.
Do đó để (*) có một nghiệm âm thì 
⇔ m < 0 hoặc .
Bài tập 5: Biết tiếp tuyến của đồ thị hàm số y = ax4 + bx2 + 2 tại điểm A (-1; 1) vuông góc với đường thẳng d: x – 2y + 3 = 0. Giá trị a2 – b2 bằng
A. 13
B. -2
C. -5
D. 10
Hướng dẫn giải
Chọn C.
Ta có: d: x – 2y + 3 = 0 ⇔ 
nên 
.
Vì tiếp tuyến vuông góc với d nên phải có hệ số góc bằng -2.
Ta có y’ = 4ax3 + 2bx = 2x (2ax2 + b)
Vì điểm A (-1; 1) là tiếp điểm của tiếp tuyến với đồ thị nên x = -1 là nghiệm của phương trình
2x (2ax2 + b) = -2 ⇒ -2 (2a + b) = -2 ⇔ 2a + b = 1.
Mặt khác điểm A thuộc đồ thị hàm số nên a + b + 2 = 1 ⇔ a + b = -1.
Vậy ta có hệ 
.
Bài tập 6: Cho hàm số y = x3 – 3x2 – 9x + 1 có đồ thị là (C). Số tiếp tuyến của (C) tạo với đường thẳng d: y = -x + 1 một góc ⍺ thỏa mãn 
là
A. 1
B. 2
C. 3
D. 4
Hướng dẫn giải
Chọn D.
Gọi k là hệ số góc của tiếp tuyến cần tìm.
Ta có 
.
Vì d có hệ số góc bằng -1 nên 
.
Ta có y’ = 3x2 – 6x – 9.
Trường hợp 1: k = – 9 ⇔ x2 – 2x = 0 ⇔ 
.
Từ đó ta tìm được hai tiếp tuyến y = -9x + 1 và y = -9x – 3.
Trường hợp 2: 
.
Từ đó ta tìm được hai tiếp tuyến là 
Vậy có bốn tiếp tuyến cần tìm.
Bài tập 7: Cho hàm số 
có đồ thị (C). Có bao nhiêu điểm A thuộc đồ thị (C) sao cho tiếp tuyến của (C) tại A cắt (C) tại hai điểm phân biệt M (x1; y1); N (x2; y2) (M, N khác A) thỏa mãn y1 – y2 = 3 (x1 – x2)
A. 0
B. 2
C. 3
D. 1
Hướng dẫn giải
Chọn B.
Do tiếp tuyến đi qua hai điểm M (x1; y1); N (x2; y2) nên hệ số góc của tiếp tuyến là 
.
Ta có 
.
Xét phương trình 
.
Mặt khác để tiếp tuyến của hàm số trùng phương cắt đực đồ thị tại hai điểm phân biệt thì tiếp điểm A chỉ có thể chạy trong phần đồ thị từ điểm cực tiểu thứ nhất sang điểm cực tiểu thứ hai (trừ hai điểm uốn).
Khi đó phương trình y’ = 0 ⇔ x3 – 7x = 0 ⇔ 
.
Do đó hai điểm cực tiểu là 
và 
nên hoành độ của tiếp điểm 
.
Vậy chỉ có x0 = -1; x0 = -2 thỏa mãn.
Dạng 4: Viết phương trình tiếp tuyến của đồ thị hàm số 
khi biết mối quan hệ của tiếp tuyến với các đường tiệm cận của đồ thị hàm số
Phương pháp giải
Với hàm số (với c ≠ 0; ad – cd ≠ 0) thì đồ thị hàm số có hai tiệm cận là 
.
Gọi 
là giao điểm của hai đường tiệm cận (và cũng là tâm đối xứng của đồ thị).
Khi đó tiếp tuyến tại điểm M (x0; y0) bất kì của đồ thị tiệm cận đứng tại điểm 
và cắt tiệm cận ngang tại điểm 
.
Ta có 
⇒ 
là hằng số không đổi.
Suy ra 
.
Khi đó các bài toán sau là tương đương:
Tìm điểm M ∊ (C) hoặc viết phương trình tiếp tuyến của (C) biết tiếp tuyến tạo với hai tiệm cận một tam giác vuông có
Cạnh huyền nhỏ nhất
Dấu bằng xảy ra khi IA = IB.
Chu vi nhỏ nhất
Ta có 
Dấu bằng xảy ra IA = IB.
Bán kính đường tròn ngoại tiếp nhỏ nhất
Ta có 
.
Dấu bằng xảy ra khi IA = IB.
Bán kính đường tròn nội tiếp lớn nhất
Ta có 
Vậy r lớn nhất khi IA + IB + AB nhỏ nhất và bằng 
.
Dấu bằng xảy ra khi IA = IB.
Khoảng cách từ I đến tiếp tuyến lớn nhất
Gọi H là hình chiếu của I trên d, ta có 
.
Dấu bằng xảy ra khi IA = IB.
Nhận xét: Các câu hỏi trên thì đẳng thức đều xảy ra khi IA = IB nên ∆IAB vuông cân tại I.
Gọi ⍺ là góc giữa tiếp tuyến d và tiệm cận ngang ∆2 thì ⍺ = (d; ∆2) = (d; Ox) = 450 nên hệ số góc của tiếp tuyến là k = ±tan 450 = ±1.
Bài tập vận dụng
Bài tập 1: Cho hàm số 
có đồ thị (C). Có bao nhiêu cặp điểm A, B thuộc (C) mà tiếp tuyến tại đó song song với nhau?
A. Không tồn tại cặp điểm đó
B. Vô số số cặp điểm
C. 2
D. 1
Hướng dẫn giải
Chọn B.
Giả sử 
với a ≠ b; a, b ≠ 1.
Do tiếp tuyến tại A, B song song với nhau nên y’(a) = y’(b) ⇔ 
Do a ≠ b nên chỉ có a + b = 2. Vậy có vô số cặp điểm A, B thỏa mãn.
Nhận xét: Hai điểm A, B phân biệt thuộc đồ thị hàm số mà tiếp tuyến tại đó song song với nhau thì A, B đối xứng với nhau qua tâm đối xứng I.
Bài tập 2: Tiếp tuyến của đồ thị hàm số 
cùng với hai tiệm cận tạo thành một tam giác có diện tích bằng
A. 6
B. 7
C. 5
D. 4
Hướng dẫn giải
Chọn C.
Gọi M (x0; y0) là tiếp điểm của tiếp tuyến với đồ thị. Khi đó tiếp tuyến tại M cắt hai tiệm cận tại A, B và I là giao điểm của hai tiệm cận.
Theo lý thuyết đã nếu thì 
.
Bài tập 3: Cho hàm số 
có đồ thị (C). Tiếp tuyến tại điểm M (a; b) ∊ (C), a > 0 tạo với hai tiệm cận của (C) một tam giác có bán kính đường tròn ngoại tiếp bằng 
. Giá trị của a + 2b bằng
A. 2
B. 4
C. 8
D. 5
Hướng dẫn giải
Chọn C.
Gọi A, B là giao điểm của tiếp tuyến với hai đường tiệm cận và I là giao điểm của hai đường tiệm cận. Do ∆IAB vuông tại I nên bán kính đường tròn ngoại tiếp ∆IAB là 
.
Theo lý thuyết, ta có 
.
Dấu “=” xảy ra khi IA = IB. Khi đó hệ số góc tiếp tuyến k = ±1.
Mặt khác 
.
Ta có 
. Do a > 0 ⇒ a = 2 ⇒ b = 3. Vậy a + 2b = 8.
Bài tập 4: Gọi (C) là đồ thị hàm số 
, m là tham số khác -4 và d là một tiếp tuyến của (C). Gọi S là tập hợp các giá trị thực của tham số m để d tạo với hai đường tiệm cận của (C) một tam giác có diện tích bằng -2, tổng giá trị các phần tử S bằng
A. -11
B. 8
C. 3
D. -8
Hướng dẫn giải
Chọn D.
Gọi A, B lần lượt là các giao điểm của tiếp tuyến với hai đường tiệm cận và I là giao điểm của hai tiệm cận.
Theo lý thuyết, ta có 
Vậy ta có 
⇒ S = {-5; -3} nên tổng các phần tử của S bằng -8.
Bài tập 5: Gọi ∆ là tiếp tuyến tại điểm M (x0; y0), x0 <0 thuộc đồ thị của hàm số 
sao cho khoảng cách từ I (-1; 1) đến A đạt giá trị lớn nhất. Giá trị x0. y0 bằng
A. -1
B. 0
C. -2
D. 2
Hướng dẫn giải
Chọn B.
Gọi A, B là giao điểm của A với hai đường tiệm cận.
Theo lý thuyết d (I; ∆) lớn nhất khi IA = IB ⇒ k = ±1.
Mặt khác 
.
Vậy 
.
Do x0 < 0 ⇒ x0 = -2 ⇒ y0 = 0 ⇒ x0. y0 = 0.
Bài tập 6: Cho hàm số 
có đồ thị là (C). Phương trình tiếp tuyến (C) tạo với hai tiệm cận một tam giác có chu vi nhỏ nhất là
A. ∆: y = -x – 1 và ∆: y = -x + 17
B. ∆: y = -x – 1 và ∆: y = -x + 7
C. ∆: y = -x – 21 và ∆: y = -x + 7
D. ∆: y = -x – 3 và ∆: y = -x + 2
Hướng dẫn giải
Chọn B.
Gọi A, B là giao điểm của tiếp tuyến tại điểm M (x0; y0) ∊ (C) với hai tiệm cận và I là giao điểm của hai đường tiệm cận. Khi đó ∆IAB vuông tại I.
Theo lý thuyết, chu vi ∆IAB là 
vì 
Do đó chu vi nhỏ nhất bằng 
Mặt khác 
.
Vậy ta có 
.
Với x0 = 3 thì y0 = 4. Do đó phương trình tiếp tuyến là y = – (x – 3) + 4 = -x + 7
Với x0 = -1 thì y0 = 0. Do đó phương trình tiếp tuyến là y = – (x + 1) = -x – 1
Bài tập 7: Cho hàm số 
có đồ thị (C). Một tiếp tuyến bất kỳ với (C) cắt đường tiệm cận đứng và đường tiệm cận ngang của (C) lần lượt tại A và B, biết I (1; 2). Giá trị lớn nhất của bán kính đường tròn nội tiếp tam giác IAB bằng
A. 
B. 
C. 
D. 
Hướng dẫn giải
Chọn C.
Gọi A, B là giao điểm của tiếp tuyến tại điểm M (x0; y0) ∊ (C) với hai tiệm cận và I là giao điểm của hai đường tiệm cận. Khi đó ∆IAB vuông tại I.
Theo lý thuyết, ta có 
.
Khi đó bán kính đường tròn nội tiếp ∆IAB lớn nhất xảy ra khi
⇒ 
Bài tập 8: Cho hàm số 
có đồ thị (C). Phương trình tiếp tuyến của (C) tạo với hai trục tọa độ một tam giác có diện tích bằng 
là
A. 
B. 
C. 
D. 
Hướng dẫn giải
Chọn A.
Gọi 
là tiếp điểm của tiếp tuyến. Khi đó phương trình tiếp tuyến d của (C) tại M là 
Gọi A, B lần lượt là các giao điểm của d với hay truc Ox, Oy.
Tọa độ các điểm A, B lần lượt là 
.
Vậy 
.
Với 
Với 
Bài tập 9: Cho hàm số 
có đồ thị (C). Gọi M (x0; y0), x0 > 0 là điểm thuộc (C), biết tiếp tuyến của (C) tại M cắt tiệm cận đứng và tiệm cận ngang lần lượt tại A và B sao cho S∆OIB = 8 S∆OIA (I là giao hai đường tiệm cận). Giá trị biểu thức S = x0 – 4y0 bằng
A. 
B. -2
C. 2
D. 
Hướng dẫn giải
Chọn B.
Do góc 
nên 
.
Mà 
nên 
.
Mặt khác 
.
⇔ 
.
Do x0 > 0 nên x0 = 3 ⇒ 
.
Bài tập 10: Cho hàm số 
có đồ thị (C). Phương trình tiếp tuyến tại điểm M thuộc (C) cắt tiệm cạn đứng và tiệm cận ngang lần lượt tại A, B sao cho côsin góc 
bằng 
với I (2; 2) là
A. 
B. 
C. 
D. 
Hướng dẫn giải
Chọn D.
Ta có 
Giả sử M (x0; y0) ∊ (C) thì 
.
Xét phương trình 
.
Với x0 = 0 thì 
. Phương trình tiếp tuyến là 
.
Với x0 = 4 thì 
. Phương trình tiếp tuyến là 
.
Dạng 5: Lập phương trình tiếp tuyến của đồ thị hàm số y = f(x) đi qua điểm M (x0; y0) cho trước.
Phương pháp giải
Thực hiện một trog hai cách sau
Cách 1
– Bước 1. Giả sử tiếp tuyến có hệ số góc k, khi đó phương trình tiếp tuyến có dạng y = k (x – x0) + y0.
– Bước 2. Tìm k là nghiệm của hệ phương trình
Từ đó suy ra phương trình của tiếp tuyến.
Cách 2
– Bước 1. Giả sử A (a; f(a)) là tiếp điểm của tiếp tuyến với đồ thị hàm số đã cho nên phương trình tiếp tuyến tại điểm A là y = f’(a) (x – a) + f(a).
– Bước 2. Do tiếp tuyến đi qua M (x0; y0) nên a là nghiệm của phương trình f’(a) (x – a) + f(a) = y0.
Tìm a và suy ra phương trình tiếp tuyến.
Bài tập vận dụng
[ads]
Dạng 6: Xác định các điểm M để có k tiếp tuyến của đồ thị hàm số (C): y = f(x) đi qua điểm M
Phương pháp giải
Thực hiện theo các bước sau
– Bước 1. Xây dựng tọa độ điểm M (a; b).
– Bước 2. Giả sử d là đường thẳng đi qua M và có hệ số góc k. Khi đó phương trình đường thẳng
d: y = k (x – a) + b.
– Bước 3. Để d là tiếp tuyến của (C) thì hệ phương trình (*) 
có nghiệm.
Dựa vào số nghiệm của hệ trên suy ra số tiếp tuyến tương ứng bài toán yêu cầu.
Nhận xét
– Nếu f(x) là hàm số bậc 2, bậc 3, bậc nhất trên bậc nhất thì hệ (*) có bao nhiêu nghiệm thì tương ứng với bấy nhiêu tiếp tuyến.
– Nếu f(x) là hàm số trùng phương có 3 điểm cực trị thì nếu hệ (*) có nghiệm không phải là hoành độ của 2 điểm cực tiểu (cực đại) thì mỗi nghiệm ứng với một tiếp tuyến của đồ thị (C).
Bài tập vận dụng
Dạng 7: Lập phương trình tiếp tuyến của đồ thị hàm số ẩn tại điểm có hoành độ x = x0 cho trước
Phương pháp giải
Từ biểu thức của hàm ẩn, tìm các tính các giá trị y0 = f(x0) và f’(x0).
Áp dụng công thức viết phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm có hoành độ x = x0.
Chú ý công thức đạo hàm của hàm số hợp: Cho hàm số f(x) có đạo hàm trên khoảng K, u = u(x) là hàm số xác định và có đạo hàm trên K và có giá trị trên khoảng K. Khi đó (f(u))’ = u’. f’(u).
Bài tập vận dụng
Bài tập 1: Cho hàm số y = f(x) có đạo hàm liên tục trên ℝ thỏa mãn 2 f (2x) + f (1 – 2x) = 12x2, ∀x ∊ ℝ. Phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm có hoành độ bằng 1 là
A. y = 2x + 2
B. y = 4x – 6
C. y = 2x – 6
D. y = 4x – 2
Hướng dẫn giải
Chọn D.
Ta cần tính f (1), f’ (1).
Từ giả thiết 2 f (2x) + f (1 – 2x) = 12x2, ∀x ∊ ℝ. (*)
Chọn x = 0 và 
, ta được 
.
Lấy đạo hàm hai vế (*) ta được 4. f’(2x) – 2. F’ (1 – 2x) = 24x, ∀x ∊ ℝ
Chọn x = 0 và , ta được 
.
Vậy f (1) = 2; f’ (1) = 4 nên phương trình tiếp tuyến là y = 4 (x – 1) + 2 = 4x – 2.
Bài tập 2: Cho các hàm số y = f(x), y = g(x)= f (f(x)), y = h(x) = f (x3 +2) có đạo hàm trên ℝ và có đồ thị lần lượt là (C1), (C2), (C3). Đường thẳng x = 2 cắt (C1), (C2), (C3) lần lượt tại A, B, C. Biết phương trình tiếp tuyến của (C1) tại A và của (C2) tại B lần lượt là y = 3x + 4 và y = 6x + 13. Phương trình tiếp tuyến của (C3) tại C là
A. y = 24x – 23
B. y = 10x – 21
C. y = -12x + 49
D. y = 2x – 5
Hướng dẫn giải
Chọn A.
Để giải bài toán, ta cần tính h’ (2) và h (2).
Phương trình tiếp tuyến của (C1) tại A là
y = f’ (2). (x – 2) + f (2) = 3x + 4 ⇒ 
.
Phương trình tiếp tuyến của (C2) tại B là
y = f’ (2). f’ (f (2) (x – 2) + f (f (2)) = f’ (2). f’ (10) (x – 2) + f (10) = 6x + 13.
⇒ 
.
Ta có h’ (x) = (f (x3 + 2))’ = 3x2. f’ (x3 + 2) nên h’ (2) = 12 f’ (10) = 24 và h (2) = f (10) = 25.
Phương trình tiếp tuyến của (C3) tại C là
y = h’ (2) (x – 2) + h (2) = 24 (x – 2) + 25 = 24x – 23.
Bài tập 3: Cho hàm số y = f(x) xác định có đạo hàm và nhận giá trị dương trên ℝ. Biết tiếp tuyến của hai đồ thị hàm số y = f(x) và y = g(x)= 
cùng tại điểm có hoành độ x0 = 1 có hệ số góc lần lượt là 12 và -3. Giá trị của f (1) bằng
A. 3
B. 4
C. 6
D. 2
Hướng dẫn giải
Chọn B.
Ta có 
Từ giả thiết ta có f’ (1) = 12 và g’ (1) = -2, f(x) > 0, ∀x ∊ ℝ
⇒ 
.
Bài tập 4: Cho hàm số y = f(x) có đạo hám liên tục trên ℝ. Gọi ∆1, ∆2 lần lượt là tiếp tuyến của đồ thị hàm số y = f(x) và y = g(x)= x2. f (4x – 3) tại điểm có hoành độ x = 1. Biết hai đường thẳng ∆1, ∆2 vuông góc với nhau và ∆1 không song song với Ox, Oy. Mệnh đề nào sau đây đúng?
A. 
B. |f (1) | < 2
C. |f (1) | ≥ 2
D. 
Hướng dẫn giải
Chọn C
Ta có g’(x) = (x2. f (4x – 3))’ = 2x. f (4x – 3) + 4x2. f’ (4x – 3).
Ta có hệ số góc của các tiếp tuyến ∆1, ∆2 lần lượt là f’ (1) và g’ (1) = 2 f (1) + 4 f’ (1).
Theo giả thiết thì f’ (1). g’ (1) = -1 và f’ (1) ≠ 0.
⇔ f’ (1). (2 f (1) + 4 f’ (1)) = -1
⇔ 
.
Bài tập 5: Cho hàm số y = f(x) có đạo hàm f’ (x) trên ℝ thỏa mãn f (x3 + 3x + 1) = 2x – 1 với mọi x ∊ ℝ. Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x = -3 là
A. 
B. 
C. 
D. 
Hướng dẫn giải
Chọn B.
Để viết phương trình tiếp tuyến tại điểm x = -3, ta cần tính f (-3) và f’ (-3).
Với x = -1 suy ra f (-3) = -3.
Do f (x3 + 3x + 1) = 2x – 1 ⇒ (3x2 + 3) f’ (x3 + 3x + 1) = 2.
Với x = -1 ⇒ 6 f’ (-3) = 2 ⇒ 
.
Do đó phương trình tiếp tuyến cần tìm là
y = f’ (-3) (x + 3) + f (-3) ⇔ 
.
Bài tập 6: Cho hàm số y = f(x) có đạo hàm trên ℝ. Gọi (C1), (C2) và (C3) lần lượt là đồ thị của các hàm số f(x), g(x) = f (x2) và h(x) = f (x3). Biết f (1) = 1 và tổng hệ số góc của hai tiếp tuyến tại điểm có hoành độ x = 1 của (C1), (C2) bằng -3. Phương trình tiếp tuyến của (C3) tại điểm có hoành độ x = 1 là
A. y = -x + 2
B. y = -3x – 2
C. y = -x – 1
D. y = -3x + 4
Hướng dẫn giải
Chọn D.
Ta cần tính h (1), h’ (1).
Ta có g’ (x) = 2xf’ (x2), h’ (x) = 3x2f’ (x3).
Theo giả thiết, ta có f’ (1) + g’ (1) = -3 ⇔ f’ (1) + 2f’ (1) = -3 ⇔ f’ (1) = -1.
Do đó h’ (1) = 3 f’ (1) = -3 và h (1) = f (1) = 1.
Vậy phương trình tiếp tuyến cần tìm là y = -3 (x – 1) + 1 = -3x + 4.
Bài tập 7: Cho hai hàm số f(x), g(x) đều có đạo hàm trên ℝ và thỏa mãn f3 (2 – x) – 2 f2 (2 + 3x) + x2 g(x) + 36x = 0, với mọi x ∊ ℝ. Phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm có hoành độ x = 2 là
A. y =-x
B. y = 2x – 3
C. y = -2x +3
D. y = x
Hướng dẫn giải
Chọn D.
Ta có f3 (2 – x) – 2 f2 (2 + 3x) + x2 g(x) + 36x = 0, ∀x ∊ ℝ (1)
Thay x = 0 vào (1) ta có 
Lấy đạo hàm hai vế của (1) ta được
-3f2 (2 – x). f’ (2 – x) – 12f (2 + 3x). f’ (2 + 3x) + 2x. g(x) + x2. g’ (x) + 26 = 0 (2).
Thay x = 0 vào (2) ta có -3f2 (2). f’ (2) – 12f (2). f’ (2) + 36 = 0 (3).
Với f (2) = 0 thay vào 3 thì 36 = 0 (vô lý).
Với f (2) = 2 thay vào (3) thì f’ (2) = 1 nên phương trình tiếp tuyến là y = x.
Bài tập 8: Cho hàm số y = f(x) có có đạo hàm liên tục trên ℝ thỏa mãn [f(x)]3 + 6f(x) = -3x + 10 với mọi x ∊ ℝ. Phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm có hoành độ x = 1 là
A. y = -x + 2
B. y = x
C. 
D. 
Hướng dẫn giải
Chọn D.
Ta cần tính f (1), f’ (1).
Thay x = 1 vào đẳng thức [f(x)]3 + 6f(x) = -3x + 10, ta có
[f (1)]3 + 6f (1) = -3x + 10 ⇔ [f (1)]3 + 6f (1) – 7 = 0 ⇔ f (1) = 1.
Theo bài ra ta có [f(x)]3 + 6f(x) = -3x + 10 đúng với mọi x nên đạo hàm hai vế ta được
3.[f(x)]2. f’ (x) + 6f’ (x) = -3, ∀x ∊ ℝ.
Thay x = 1 vào ta có 3. [f (1)]2. f’ (1) + 6f’ (1) = -3.
Vì f (1) = 1 nên 
.
Vậy phương trình tiếp tuyến cần tìm là .
.
Dạng 8: Tìm các điểm trên đồ thị hàm số y = f(x) mà tiếp tuyến tại các điểm đó song song với nhau hoặc có cùng hệ số góc k.
Phương pháp giải
Giả sử hai điểm A (xA; f (xA)), B (xB; f (xB)) (xA ≠ xB) thuộc đồ thị hàm số y = f(x) mà tiếp tuyến tại hai điểm đó song song với nhau hoặc có cùng hệ số góc k thì xA, xB là hai nghiệm của phương trình f’ (x) = k.
Khi đó ta có biểu thức liên hệ giữa xA, xB. Từ đó giải quyết yêu cầu bài toán đưa ra.
Đối với hàm số 
có tâm đối xứng là 
. Nếu A, B là hai điểm thuộc đồ thị tiếp tuyến tại A, B song song với nhau thì I là trung điểm AB.
Bài tập
[ads]
Bài tập 1: Cho hàm số 
có đồ thị (H). Gọi A (x1; y1), B (x2; y2) là hai điểm phân biệt thuộc (H) sao cho tiếp tuyến của (H) tại A, B song song với nhau. Độ dài nhỏ nhất của đoạn thẳng AB bằng
A. 
B. 
C. 
D. 
Hướng dẫn giải
Chọn C.
Ta có 
. Do tiếp tuyến của (H) tại A, B song song với nhau nên 
Vì x1 ≠ x2 nên x1 + x2 = 1.
Khi đó do vai trò của A, B như nhau nên ta có thể giả sử 
thì 
.
Gọi 
là giao điểm của hai đường tiệm cận.
Ta thấy 
nên I là trung điểm của AB.
Ta có 
Vì I là trung điểm của AB nên 
.
Vậy 
.
Bài tập 2: Cho hàm số 
có đồ thị (H). Gọi A (x1; y1), B (x2; y2) là hai điểm phân biệt thuộc (H) sao cho tiếp tuyến của (H) tại A, B có cùng hệ số góc k. Biết diện tích tam giác OAB bằng 
. Mệnh đề nào dưới dây đúng?
A. k < -9
B. -9 ≤ k < -6
C. -6 ≤ k < -3
D. -3 ≤ k < 0
Hướng dẫn giải
Chọn D.
Ta có 
Tiếp tuyến tại A, B của (H) có cùng hệ số góc k nên x1, x2 là hai nghiệm phân biệt của phương trình 
.
Suy ra 4kx2 – 4kx + k + 3 = 0 (*) nên 
.
Khi đó do vai trò của A, B như nhau nên ta có thể giả sử 
thì 
.
Áp dụng công thức tính diện tích tam giác ABC nếu có 
thì 
.
Ta có 
.
⇒ 
.
⇔ 
(vì a > 0).
Với a = 3 ⇒ x1 = 2; x2 = -1 ⇒ 
.
Với a = 1 ⇒ x1 = 1; x2 = 0 ⇒ k = -3.
Vậy giá trị của k là k = -3; .
Bài tập 3: Cho hàm số y = x3 – 3x + 1 có đồ thị (C). Gọi A (xA; yA), B (xB; yB) với xA > xB là các điểm thuộc (C) sao cho tiếp tuyến tại A, B song song với nhau và 
. Giá trị 2xA – 3xB bằng
A. 15
B. 90
C. -15
D. -90
Hướng dẫn giải
Chọn A.
Ta có y’ = 3x2 – 3.
Do tiếp tuyến của (C) tại A, B song song với nhau nên y’ (xA) = y’ (xB)
⇔ 3x2A – 3 = 3x2B – 3 ⇔ xA + xB = 0 (do xA > xB).
Giả sử A (a; a3 – 3a + 1), B (-a; -a3 + 3a + 1) với a > 0 thuộc (C).
Khi đó 
⇔ 4a6 – 24a4 + 40a2 – 1332 = 0 ⇔ a2 = 9 ⇒ a = 3 (vì a > 0)
⇒ xA = 3; xB = -2 nên 2xA – 3xB = 15.
Bài tập 4: Cho hàm số 
có đồ thị (C). Gọi A, B là hai điểm phân biệt thuộc (C) và tiếp tuyến của (C) tại A, B song song với nhau. Đường thẳng AB cắt các trục Ox, Oy lần lượt tại M, N diện tích tam giác OMN bằng 
. Độ dài đoạn MN bằng
A. 
B. 
C. 
D. 
Hướng dẫn giải
Chọn B.
Ta có 
. Gọi A (x1; y1), B (x2; y2).
Khi đó y’ (x1) = y’ (x2) ⇔ (x1 – 1)2 = (x2 – 1)2 ⇔ x1 + x2 = 2.
Do đó tâm đối xứng I (1; 1) của (C) là trung điểm của đoạn thẳng AB.
Gọi hệ số góc của đường thẳng AB là k.
Phương trình đường thẳng AB là y = k (x – 1) + 1.
Điều kiện để đường thẳng d: y = k (x – 1) + 1 cắt (C) tại hai điểm phân biệt A, B là phương rình 
có hai nghiệm phân biệt x ≠ 1.
Ta có (*) ⇔ kx2 – 2kx + k – 3 = 0 có hai nghiệm phân biệt x ≠ 1 khi và chỉ khi 
Vì M, N là giao điểm của AB với Ox, Oy nên 
.
Suy ra 
Ta có 
Với 
.
Với 
.
Vậy trong cả hai trường hợp thì MN = .
Dạng 9: Một số dạng toán khác
Phương pháp giải
Với các dạng toán xác định phương trình tiếp tuyến không nằm trong 8 dạng bên trên,các bài toán thường có yếu tố độ dài, lớn nhất nhỏ nhất ta lần lượt tiến hành theo các bước:
- Tìm nghiệm của phương trình đạo hàm của hàm số đã cho
- Canh vào điều kiện của bài toán để tiếp tục
Bài tập vận dụng
Bài tập 1: Gọi A là điểm thuộc đồ thị (C) của hàm số y = x4 – 3x2 + 2 và có hoành độ a. Có bao nhiêu số nguyên a sao cho tiếp tuyến của (C) tại A cắt (C) tại hai điểm phân biệt B, C khác A?
A. 1
B. 3
C. 2
D. 5
Hướng dẫn giải
Chọn B.
Ta có 
y’’ = 12x2 – 6; y’’ = 0 ⇔ 
.
Tọa độ các điểm có hoành độ a nguyên để tiếp tuyến tại điểm đó cắt trục hoành tại hai điểm thỏa mãn 
.
Vậy có ba giá trị nguyên của a thỏa mãn.
Nhận xét: Đối với đồ thị hàm số y = ax4 + bx2 + c mà đồ thị có ba điểm cực trị (khi ab < 0) thì tiếp tuyến của đồ thị tại các điểm có hoành độ nằm giữa hai điểm cực tiểu (cực đại), trừ điểm uốn luôn cắt đồ thị tại hai điểm khác nữa.
Bài tập 2: Gọi A là điểm thuộc đồ thị (C) của hàm số y = x4 – 3x2 + 2 và có hoành độ a. Có bao nhiêu số nguyên a sao cho tiếp tuyến của (C) tại A cắt (C) tại hai điểm phân biệt B, C khác A và diện tích tam giác OBC bằng 
?
A. 1
B. 3
C. 2
D. 5
Hướng dẫn giải
Chọn A.
Ta có 
.
y’’ = 12x2 – 6; y’’= 0 ⇔ 
.
Tọa độ các điểm có hoành độ a nguyên để tiếp tuyến tại điểm đó cắt trục hoành tại hai điểm nữa thì 
.
Với a = -1 ⇒ A (-1; 0). Khi đó phương trình tiếp tuyến là y = 2 (x + 1).
Xét phương trình 
nên B (0; 2), C (2; 6) ⇒ S∆OBC = 2 (loại).
Với a = 0 ⇒ A (0; 2). Khi đó phương trình tiếp tuyến là y = 2 nên 
(thỏa mãn).
Với a = 1 ⇒ A (1; 0). Khi đó phương trình tiếp tuyến là y = -2 (x – 1) nên B (0; 2), C (-2; 6) ⇒ S∆OBC = 2 (loại).
Vậy a = 0.
Bài tập 3: Cho hàm số 
có đồ thị (C). Gọi S là tập hợp tất cả các giá trị thực của m sao cho tiếp tuyến của (C) tại điểm có hoành độ x = m – 2 cắt tiệm cận đứng tại A (x1; y1), cắt tiệm cận ngang tại B (x2; y2) thỏa mãn x2 + y1 = -5. Tổng giá trị các phần tử của S bằng
A. 4
B. -2
C. -4
D. 2
Hướng dẫn giải
Chọn B.
Đồ thị (C) có tiệm cận đứng và tiệm cận ngang lần lượt là x = -2 và y = 1.
Ta có 
.
Gọi 
, tiếp tuyến của (C) tại M có phương trình là 
.
Giao điểm của tiếp tuyến với tiệm cận đứng là 
và tiệm cận ngang là B (2m – 2; 1).
Theo gia thiết ta có 
.
Vậy m1 + m2 = -2.
Bài tập 4: Cho hàm số 
có đồ thị (C). Gọi A, B là hai điểm nằm trên hai nhánh của (C) và các tiếp tuyến của (C) tại A, B cắt các đường tiệm cận ngang và tiệm cận đứng lần lượt tại các cặp M, N và P, Q. Diện tích tứ giác MNPQ nhỏ nhất bằng
A. 16
B. 32
C. 8
D. 4
Hướng dẫn giải
Chọn A.
Gọi I là giao điểm của hai đường tiệm cận. Theo tính chất của tiếp tuyến đồ thị hàm số bậc nhất trên bậc nhất thì IM. IN = IP. IQ = 8.
Ta có 
.
= 
.
Vậy 
tức là MNPQ là hình vuông.
Bài tập 5: Cho hàm số 
có đồ thị (C). Có bao nhiêu giá trị nguyên của tham số m để có ít nhất hai tiếp tuyến của (C) song song hoặc trùng với đường thẳng d: y = mx?
A. 27
B. 28
C. 26
D. 25
Hướng dẫn giải
Chọn B.
Giả sử M (a; b) là tiếp điểm. Ta có y’ = 2x3 – 3x2 – 12x.
Tiếp tuyến của (C) tại M song song hoặc trùng với đường thẳng d: y = mx nên a là nghiệm của phương trình 2x3 – 3x2 – 12x = m (*).
Để có ít nhất hai tiếp tuyến của (C) song song hoặc trùng với đường thẳng d thì phương trình (*) có ít nhất hai nghiệm.
Xét f(x) = 2x3 – 3x2 – 12x có y’ = 6x2 – 6x – 12; y’ = 0 ⇔ 
.
Bảng biến thiên
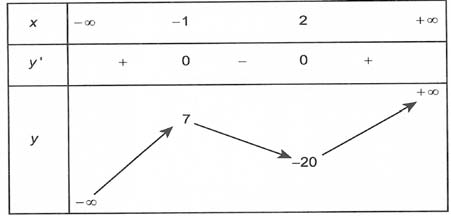
Từ bảng biến thiên, để phương trình (*) có ít nhất hai nghiệm thì -20 ≤ m ≤ 7.
Mà m ∊ ℤ nên m ∊ {-20, -19, …, 6, 7}.
Vậy có 28 giá trị m thỏa mãn.
Bài tập 6: Cho đường cong (C): H320 và điểm I (1; 1). Hai điểm A và B thuộc cùng một nhánh của đồ thị sao cho IA = IB. Gọi k1 và k2 lần lượt là hệ số góc của tiếp tuyến tại A và B. Khi tiếp tuyến tại A và B của (C) tạo với nhau một góc 150, giá trị biểu thức |k1 + k2| bằng
A. 
B. 
C. 
D. 
Hướng dẫn giải
Chọn A.
Do IA = IB nên k1. k2 = 1.
Ta có 
⇔ 
⇔ 
⇔ 
.
Nhận xét: Đối với đồ thị hàm số 
có tâm đối xứng là I. Cho A, B là hai điểm thuộc cùng một nhánh của đồ thị hàm số thỏa mãn IA = IB.
Gọi k1, k2 là hệ số góc của tiếp tuyến của đồ thị hàm số đã cho tại A, B.
Ta có 
.
Tài liệu phương trình tiếp tuyến
1. Thông tin tài liệu
| Thông tin | |
| Tên tài liệu | Chuyên đề phương trình tiếp tuyến của hàm số |
| Tác giả | verbalearn.org |
| Số trang | 58 |
2. Mục lục
- Phần lý thuyết trọng tâm
- Dạng 1: Lập phương trình tiếp tuyến của đồ thị hàm số tại điểm cho trước
- Dạng 2: Lập phương trình tiếp tuyến của đồ thị hàm số y = f(x) khi biết hệ số góc
- Dạng 3: Lập phương trình tiếp tuyến của đồ thị hàm số y = f(x) đi qua điểm M cho trước
- Dạng 4: Lập phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x = xo cho trước
- Dạng 5: Một số bài toán tiếp tuyến nâng cao
3. Xem tài liệu
[ads]
Nguồn tham khảo
Cấp Nước Lào Cai chỉ sử dụng các nguồn tham khảo chất lượng cao, bao gồm các nghiên cứu được đánh giá cùng chuyên mục để hỗ trợ các dữ liệu trong bài viết. Từ đó luôn giữ cho nội dung trên website chính xác và đáng tin cậy nhất. Mang thêm nguồn thông tin hữu ích đến bạn đọc thông qua các nguồn được nghiên cứu.
Câu hỏi thường gặp
Tiếp tuyến là gì?
Tiếp tuyến của một đường cong tại một điểm bất kỳ thuộc đường cong là đường thẳng chỉ “chạm” vào đường cong tại điểm đó. Nhà toán học Leibniz định nghĩa tiếp tuyến như một đường thẳng nối một cặp điểm gần nhau vô hạn trên đường cong.
Có những dạng bài tập phương trình tiếp tuyến nào?
Việc phân chia dạng phương trình tiếp tuyến tùy thuộc vào từng mục đích khác nhau. Ở đây Cấp Nước Lào Cai có thể giúp bạn phân tích thành 5 dạng bài đặc trưng như sau: Lập phương trình tiếp tuyến tại điểm cho trước, khi biết hệ số góc, đi qua một điểm cho trước, tại điểm có hoành độ cho trước, bài toán có yếu tố độ dài hoặc lớn nhất nhỏ nhất.
Bạn đang xem bài viết Phương trình tiếp tuyến | Phân dạng & cách giải chi tiết (Có tài liệu) xem thêm các bài viết khác về chủ đề Toán lớp 11. Chúc bạn 1 ngày vui vẻ!
