Bạn đang xem bài viết Lý thuyết & bài tập. Hi vọng sẽ là đáp án bạn ưng ý. Cùng theo dõi nhé!
Ở bài viết này Cấp Nước Lào Cai sẽ giúp bạn tìm hiểu chi tiết lý thuyết và một số dạng bài tập hình học không gian về đường thẳng song song với mặt phẳng.
Lý thuyết đường thẳng song song với mặt phẳng
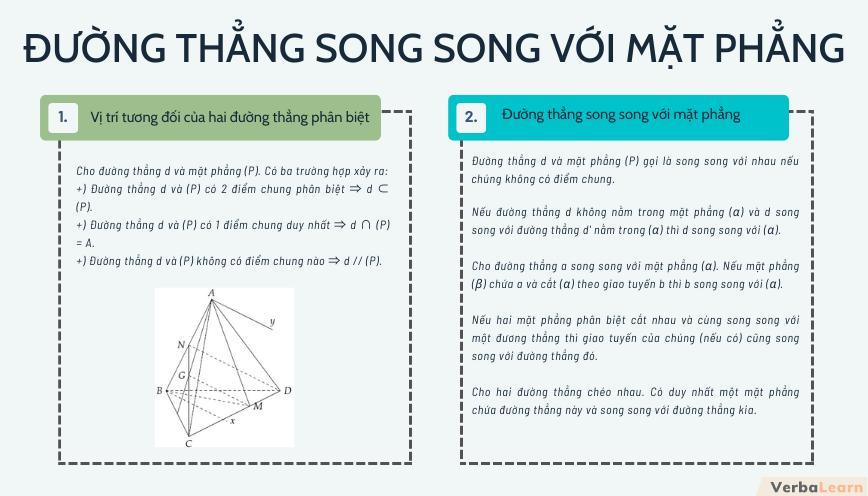
1. Vị trí tương đối của hai đường thẳng phân biệt
Cho đường thẳng d và mặt phẳng (P). Có ba trường hợp xảy ra:
+) Đường thẳng d và (P) có 2 điểm chung phân biệt ⇒ d ⊂ (P).
+) Đường thẳng d và (P) có 1 điểm chung duy nhất ⇒ d ∩ (P) = A.
+) Đường thẳng d và (P) không có điểm chung nào ⇒ d // (P).
Định nghĩa 1. Đường thẳng d và mặt phẳng (P) gọi là song song với nhau nếu chúng không có điểm chung.
Các định lý
Định lí 1. Nếu đường thẳng d không nằm trong mặt phẳng (α) và d song song với đường thẳng d’ nằm trong (α) thì d song song với (α).
Định lí 2. Cho đường thẳng a song song với mặt phẳng (α). Nếu mặt phẳng (β) chứa a và cắt (α) theo giao tuyến b thì b song song với (α).
Hệ quả 1. Nếu hai mặt phẳng phân biệt cắt nhau và cùng song song với một đương thẳng thì giao tuyến của chúng (nếu có) cũng song song với đường thẳng đó.
Định lí 3. Cho hai đường thẳng chéo nhau. Có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.
Dạng 1. Chứng minh dường thẳng a song song với mặt phẳng (P)
Phương pháp giải
Chứng minh
Bài tập vận dụng
Câu 1. Cho tứ diện ABCD. Gọi M vàN lần lượt là trọng tâm của các tam giác ACD và BCD. Chứng minh rằng MN song song với các mặt phẳng (ABC) và (ABD).
Lời giải
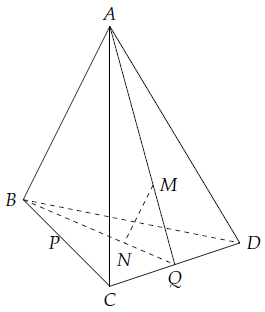
Gọi P, Q lần lượt là trung điểm của BC và CD.
Khi đó, ta có:
Vì nên MN // (ABC)
Tương tự, ta có:
nên MN // (ABD)
Câu 2. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh AB và CD.
a) Chứng minh MN song song với các mặt phẳng (SBC) và (SAD).
b) Gọi E là trung điểm của SA. Chứng minh SB và SC đều song song với mặt phẳng (MNE).
Lời giải
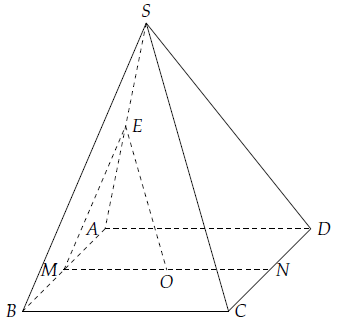
a) Từ giả thiết, ta suy ra MN // BC và MN // AD.
Vì nên MN // (SBC)
Tương tự, ta có:
nên MN // (SAD).
b) Từ giả thiết, ta có:
Vì nên SB // (MNE)
Tương tự, gọi O là tâm của hình bình hành.
Khi đó:
Vì nên SC // (MNE)
Dạng 2. Tìm giao tuyến của hai mặt phẳng
Phương pháp giải
Áp dụng một trong hai cách sau:
Cách 1:
Cách 2:
Bài tập vận dụng
Câu 1. Cho tứ diện ABCD có G là trọng tâm ∆ABC, M ∈ CD với MC = 2MD.
a) Chứng minh MG // (ABD).
b) Tìm (ABD) ∩ (BGM).
c) Tìm (ABD) ∩ (AGM).
Lời giải
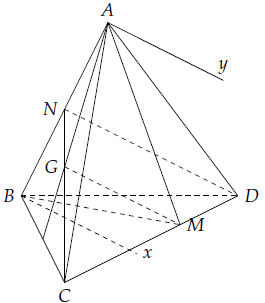
a) Gọi N là trung điểm của AB. Trong tam giác CDN, ta có:
Vì ND ⊂ (ABD), GM ⊄ (ABD) nên GM // (ABD).
b) Vì
⇒ (ABD) ∩ (BGM) = Bx // GM // ND.
c) Vì
⇒ (ABD) ∩ (BGM) = Ay // GM // ND.
Dạng 3. Tìm thiết diện song song với một đường thẳng
Phương pháp giải
Để tìm thiết diện của mặt phẳng song song với mặt phẳng (α) đi qua một điểm và song song với hai đường thẳng chéo nhau hoặc (α) chứa một đường thẳng và song song với một đường thẳng sử dụng tích chất sau:
Câu 1. Cho tứ diện ABCD. Gọi M, I lần lượt là trung điểm của BC, AC. Mặt phẳng (P) đi qua điểm M, song song với BI và SC. Xác định trên hình vẽ các giao điểm của (P) với các cạnh AC, SA, SB. Từ đó suy ra thiết diện của (P) cắt hình chóp.
Lời giải
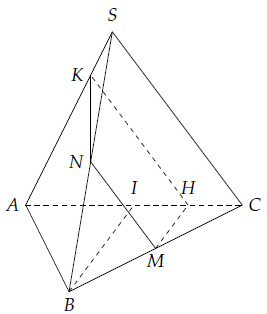
Vì
⇒ (P) ∩ (SBC) = MN // SC, N ∈ SB (1)
Tương tự,
⇒ (P) ∩ (ABC) = MH // BI, H ∈ AC (2)
Mặt khác,
⇒ (P) ∩ (SAC) = HK // SC, K ∈ SA (3)
Từ (1), (2) và (3) ta có thiết diện của (P) với tứ diện ABCD là tứ giác MNKH.
Câu 2. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm SA, SD. Chứng minh rằng:
a) BC // (SAD).
b) AD // (SBC).
c) MN // (ABCD).
d) MN // (SBC).
e) MO // (SCD).
f) NO // (SBC).
Lời giải
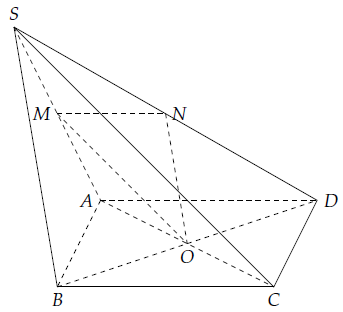
a) Ta có:
b) Ta có:
c) Ta có:
Khi đó:
d) Ta có:
Vì AD // BC nên MN // BC.
Khi đó:
e) Ta có:
Vì
f) Ta có:
Vì
Câu 3. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Gọi G là trọng tâm tam giác SAD và E là điểm trên cạnh DC sao cho DC = 3DE, I là trung điểm AD.
a) Chứng minh: OI // (SAB) và OI // (SCD).
b) Tìm giao điểm P của IE và (SBC). Chứng minh: GE // (SBC).
Lời giải
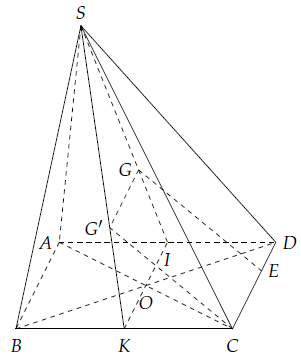
a) Ta có:
Tương tự:
b) Vì nên IE không song song với AC.
Trong hình chữ nhật ABCD, gọi P = IE ∩ BC ⇒ P = IE ∩ (SBC).
Gọi K là trung điểm của BC, G’ là trọng tâm tam giác SBC.
Khi đó:
Suy ra: G’G // KI // CE và
⇒
Do dó tứ giác G’GEC là hình bình hành, suy ra CG’ // CE
⇒ CG // (SBC).
Câu 4. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm AB và CD.
a) Chứng minh: MN // (SBC) và MN // (SAD).
b) Gọi P là trung điểm cạnh SA. Chứng minh: SB // (MNP) và SC // (MNP).
Lời giải
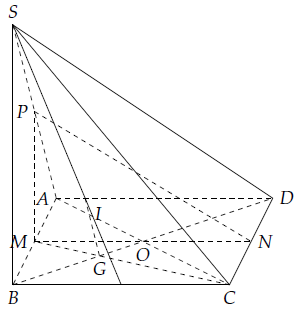
a) Từ giả thiết, ta có: MN // AD // BC.
Vì MN ⊄ (SBC), MN ⊄ (SAD)
Nên MN // (SBC) và MN // (SAD).
b) Ta có:
⇒ SB // PM ⇒ SB // (MNP)
Tương tự:
⇒ PO // SC vì OP ⊂ (MNP) nên SC // (MNP).
Câu 5. Cho hình chóp S.ABCD có đáy là hình thang đáy lớn AB, với AB = 2CD. Gọi O là giao điểm của AC và BD, I là trung điểm của SA, G là trọng tâm của tam giác SBC và E là một điểm trên cạnh SD sao cho 3SE = 2SD. Chứng minh:
a) DI // (SBC).
b) GO // (SCD).
c) SB // (ACE).
Lời giải
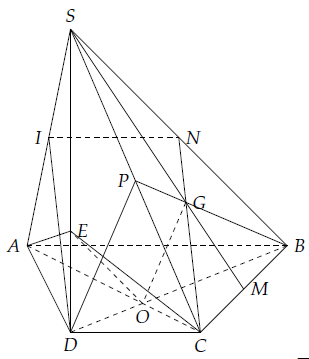
a) Gọi N là trung điểm SB, khi đó IN // AB và IN = AB.
Suy ra: IN // CD, IN = DC
Suy ra tứ giác INCD là hình bình hành.
Do đó: ID // NC.
Vậy: ID // (SBC).
b) GO // (SCD)
Gọi P là trung điểm của SC. Khi đó: GO // PD
Suy ra: GO // (SCD).
c) Ta có: EO // SB
Suy ra: SB // (ACE).
Câu 6. Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M, N là trung điểm của các cạnh AB, AD. Gọi I, J thuộc SM, SN sao cho . Chứng minh:
a) MN // (SBD).
b) IJ // (SBD).
c) SC // (IJO).
Lời giải
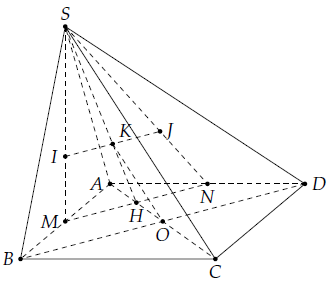
a) Ta có: M, N là trung điểm của các cạnh AB, AD.
Suy ra: MN // BD, mà BD ⊂ (SBD).
Nên: MN // (SBD).
b) Ta có:
⇒ IJ // MN hay IJ // BD.
Mà: BD ⊂ (SBD). Nên: IJ // (SBD).
c) Trong mặt phẳng (ABCD), gọi H là giao điểm của MN và AC.
Trong mặt phẳng (SMN) gọi K là giao điểm của IJ và SH.
Dễ thấy H là trung điểm của AO
Suy ra:
Lại có: IJ // MN ⇒ IK // MH
⇒
Do đó:
⇒ KO // SC
Mà: KO ⊂ (IJO) ⇒ SC // (IJO).
Câu 7. Cho tứ diện ABCD, G là trọng tâm của tam giác ABD và I là điểm trên cạnh BC sao cho BI = 2IC. Chứng minh: IG // (ACD).
Lời giải
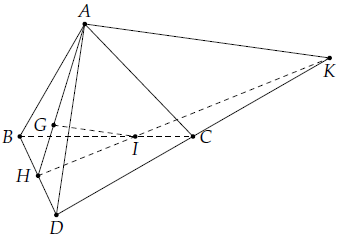
Gọi H là trung điểm của BD. Trong mặt phẳng (BCD), gọi K là giao điểm của HI và CD.
Theo định lý Menelaus có:
Suy ra: C là trung điểm của KD, suy ra BC là trung tuyến của ∆BDK.
Mà: BI = 2IC, suy ra I là trọng tâm của ∆BDK.
Suy ra: .
Lại có: G là trọng tâm của ∆ABD
Suy ra: .
Do đó, GI // AK, mà AK ⊂ (ACD) ⇒ IG // (ACD).
Câu 8. Cho tứ diện ABCD. Gọi G và P lần lượt là trọng tâm của tam giác ACD và ABC. Chứng minh rằng: GP // (BCD), GP // (ABD).
Lời giải
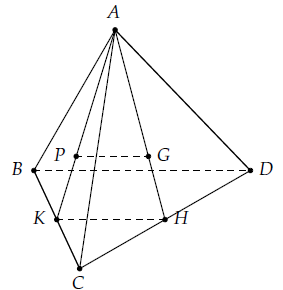
Gọi K, H lần lượt là trung điểm của BC và CD.
Suy ra: KH // BD (1).
Ta có: G, P lần lượt là trọng tâm của ∆ACD, ∆ABC.
Suy ra:
⇒ PG // HK (2).
Từ (1) và (2), suy ra: GP // BD.
Mà: BD ⊂ (BCD), BD ⊂ (ABD)
Suy ra: GP // (BCD), GP // (ABD).
Câu 9. Cho hình chóp S.ABCD có đáy là hình bình hành, O là giao điểm của AC và BD, M là trung điểm của SA.
a) Chứng minh: OM // (SCD).
b) Gọi (α) là mặt phẳng đi qua M, đồng thời song song với SC và AD. Tìm thiết diện của mặt phẳng (α) với hình chóp S.ABCD.
Lời giải
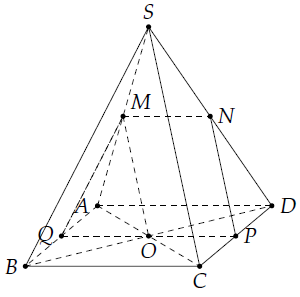
a) Ta có: M, O là trung điểm của SA và AC
Suy ra: MO // SC.
Mà: SC ⊂ (SCD) ⇒ OM // (SCD).
b) Vì MO // SC ⇒ O ∈ (α).
Ta có:
⇒ (α) ∩ (ABCD) = PQ.
Với PQ // AD, O ∈ PQ, Q ∈ AB, P ∈ CD.
Lại có:
⇒ (α) ∩ (SCD) = PN, với PN // SC.
Có: (α) ∩ (SAD) = MN, (α) ∩ (SAB) = MQ.
Nhận thấy P, Q là trung điểm của CD và AB.
Suy ra N là trung điểm của SD. Suy ra: MN // PQ.
Vậy thiết diện là hình thang MNPQ.
Câu 10. Cho hình chóp S.ABCD có đáy ABCD là hình thang đáy lớn AB. Gọi M là trung điểm của CD, (α) là mặt phẳng qua M, đồng thời song song với SA và BC. Tìm thiết diện của (α) với hình chóp S.ABCD. Thiết diện là hình gì?
Lời giải
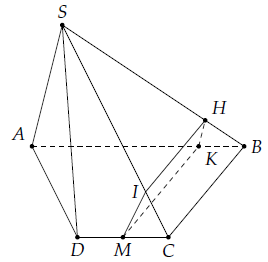
Ta có:
⇒ (α) ∩ (ABCD) = MK, với MK // BC, K ∈ AB.
Có:
⇒ (α) ∩ (SAB) = KH, với KH // SA.
Lại có:
⇒ (α) ∩ (SBC) = HI, với HI // BC.
Do đó: (α) ∩ (SCD) = IM
Mà: MK, HI đều song song với BC.
Vậy thiết diện của hình chóp là hình thang MKHI.
Câu 11. Cho hình chóp S.ABCD. Gọi M, N thuộc cạnh AB, CD. Gọi (α) là mặt phẳng qua MN và song song với SA.
a) Tìm thiết diện của (α) với hình chóp.
b) Tìm điều kiện của MN để thiết diện là hình thang.
Lời giải
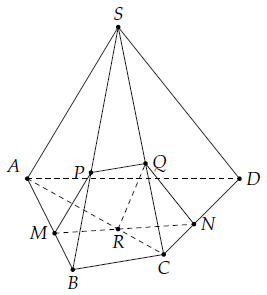
a) Ta có:
⇒ (α) ∩ (SAB) = MP, với MP // SA.
Trong mặt phẳng (ABCD), gọi R = MN ∩ AC.
Ta có:
⇒ (α) ∩ (SAC) = RQ, với RQ // SA.
Ta có: (α) ∩ (SCD) = QN.
Vậy thiết diện là tứ giác MNQP.
b) Ta có: MNQP là hình thang
⇒
Xét (1) ta có:
⇒ SA // QN.
Do đó:
⇒ SA // (SCD) (vô lý).
Xét (2) ta có:
⇒ MN // BC.
Ngược lại, nếu MN // BC thì
⇒ MN // PQ.
Vậy để thiết diện là hình thang thì MN // PQ.
Câu 12. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm của cạnh SC. (P) là mặt phẳng qua AM và song song với BD.
a) Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng (P).
b) Gọi E, F lần lượt là giao điểm của (P) với các cạnh SB, SD. Tìm tỉ số diện tích của ∆SME với ∆SBC và tỉ số diện tích của ∆SMF với ∆
c) Gọi K là giao điểm của ME và CB, J là giao của MF và CD. Chứng minh K, A, J nằm trên đường thẳng song song với EF và tìm tỉ số .
Lời giải
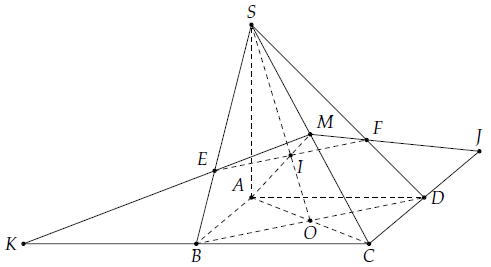
a) Trong mặt phẳng (ABCD) gọi AC ∩ BD = O.
Trong mặt phẳng (SAC), gọi AM ∩ SO = I.
Ta có:
⇒ (P) ∩ (SBD) = EF, với I ∈ EF, E ∈ SB, F ∈ SD.
Ta có: (P) ∩ (SAB) = AE
(P) ∩ (SBC) = EM
(P) ∩ (SCD) = MF.
Vậy thiết diện là tứ giác AEMF.
b) Trong ∆SAC, có I là trọng tâm của tam giác
Do đó:
c) Ta có:
⇒ K, A, J thẳng hàng.
Theo định lý Menelaus, xét ∆SBC ta có:
Hay B là trung điểm của KC.
Tương tự, ta có D là trung điểm của CJ.
Do đó, BD là đường trung bình của ∆KCJ
⇒
Mà: BD // EF.
Vậy A, K, J nằm trên đường song song với EF.
Từ (1) và (2), suy ra:
Câu 13. Cho tứ diện ABCD. Gọi M và N là hai điểm lần lượt nằm trên cạnh BC và AD. Xác định thiết diện của tứ diện cắt bởi mặt phẳng (α) qua MN và song song với CD. Xác định vị trí của hai điểm M, N để thiết diện là hình bình hành.
Lời giải
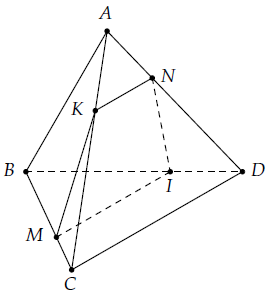
Ta có:
⇒ (α) ∩ (BCD) = MI, với MI // CD.
⇒ (α) ∩ (ACD) = NK, với NK // CD.
Ta có: (α) ∩ (ABD) = NI, (α) ∩ (ABC) = MK.
Vậy thiết diện là hình thang MINK, (vì MI // NK).
Lại có:
Để thiết diện MINK là hình bình hành khi và chỉ khi .
Vậy M, N lần lượt là hai điểm nằm trên BC và AD và .
Câu 14. Cho tứ diện ABCD. Gọi I, J lần lượt là trung điểm của AB và CD, M là một điểm trên đoạn IJ. Gọi (P) là mặt phẳng qua M và song song với AB và CD.
a) Tìm giao tuyến của mặt phẳng (P) và (ICD).
b) Xác định thiết diện của tứ diện với mặt phẳng (P). Thiết diện là hình gì?
Lời giải
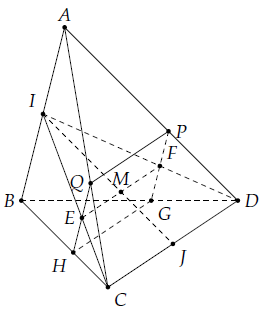
a) Gọi ∆1 = (P) ∩ (ICD), ta có:
Vậy ∆1 là đường thẳng qua M và song song với CD.
Gọi E = ∆1 ∩ IC, F = ∆1 ∩ TD, ta được (P) ∩ (ICD) = EF.
b) Gọi ∆2 = (P) ∩ (ABD), ta có:
Vậy ∆2 là đường thẳng qua F và song song với AB.
Gọi G = ∆2 ∩ BD, P = ∆2 ∩ AD, ta được (P) ∩ (ICD) = GP.
Gọi ∆3 = (P) ∩ (ABC), ta có:
Ta có:
Vậy ∆3 là đường thẳng qua E và song song với AB.
Gọi H = ∆3 ∩ BC, Q = ∆3 ∩ AC, ta được (P) ∩ (ABC) = HQ.
Giao tuyến của (P) với các mặt phẳng (BCD), (ABD), (ACD), (ABC) lần lượt là GH, GP, PQ, QH.
Do đó thiết diện của tứ diện với mặt phẳng (P) là tứ giác HGPQ.
Ta có:
Và
Ta có:
⇒ Tứ giác HGPQ là hình bình hành.
Câu 15. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi K và J lần lượt là trọng tâm của các tam giác ABC và SBC.
a) Chứng minh: KJ // (SAB).
b) Gọi (P) là mặt phẳng chứa KJ và song song với AD. Tìm thiết diện của hình chóp cắt bởi mặt phẳng (P).
Lời giải
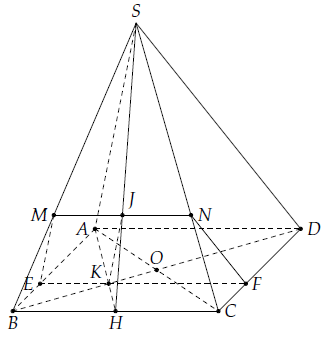
a) Gọi H là trung điểm BC, theo tính chất trọng tâm ta có:
⇒ KJ // SA (Định lý Ta-lét đảo).
Ta có:
⇒ KJ // (SAB).
b) Gọi ∆1 = (P) ∩ (ABCD), ta có:
Vậy ∆1 là đường thẳng qua K và song song với AD.
Gọi E = ∆1 ∩ AB, F = ∆1 ∩ CD, ta được: (P) ∩ (ABCD) = EF.
Gọi ∆2 = (P) ∩ (SBC), ta có:
Và:
Vậy ∆2 là đường thẳng qua J và song song với BC.
Gọi M = ∆2 ∩ SB, N = ∆1 ∩ SD, ta được: (P) ∩ (SBC) = MN.
Ta có giao tuyến của (P) với các mặt phẳng (ABCD), (SCD), (SBC), (SAB) lần lượt là EF, FN, NM, NE.
Do đó thiết diện của hình chóp cắt bởi mặt phẳng (P) là tứ giác MNFE.
Câu 16. Cho tứ diện ABCD. Gọi G1, G2 lần lượt là trọng tâm của các tam giác ACD và BCD. Chứng minh rằng: G1G2 // (ABC) và G1G2 // (ABD).
Lời giải
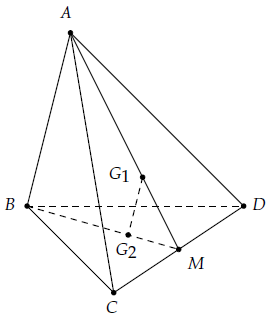
Xét tam giác ABM ta có:
(G2 là trọng tâm ∆BCD).
(G1 là trọng tâm ∆ACD).
Suy ra:
⇒ G1G2 // AB (Định lý Ta-lét đảo).
Ta có:
⇒ G1G2 // (ABC).
Ta có:
⇒ G1G2 // (ABD).
Câu 17. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi G là trọng tâm của ∆SAB, I là trung điểm AB, lấy điểm M trong đoạn AD sao cho AD = 3AM.
a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC).
b) Đường thẳng qua M và song song với AB cắt CI tại N. Chứng minh: NG // (SCD).
c) Chứng minh: MG // (SCD).
Lời giải
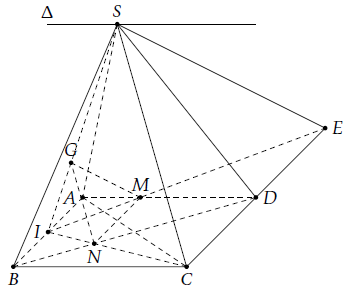
a) Gọi ∆ = (SAD) ∩ (SBC), ta có S ∈ ∆.
Ta có:
Vậy ∆ là đường thẳng qua S và song song với AD.
b) Hình thang AICD có MN // AI // CD nên
(Định lí Ta-lét).
∆SAB có G là trọng tâm nên
∆ISC có
⇒ NG // SC (Định lý Ta-lét đảo).
Ta có:
⇒ NG // (SCD).
c) Gọi E là giao điểm của IM và CD. Vì AI // DE nên ta có:
(Định lý Ta-lét).
Xét ∆ASE có
⇒ GM // SE.
Ta có:
⇒ MG // (SCD).
Câu 18. Cho hình chóp S.ABCD có đáy ABCD là hình thang với đáy lớn AD và AD = 2BC. Gọi O là giao điểm của AC và BD, G là trọng tâm của tam giác SCD.
a) Chứng minh OG k (SBC).
b) Cho M là trung điểm của SD. Chứng minh: CM // (SAB).
c) Gọi I là điểm trên cạnh SC sao cho 2SC = 3SI. Chứng minh: SA // (BDI).
Lời giải
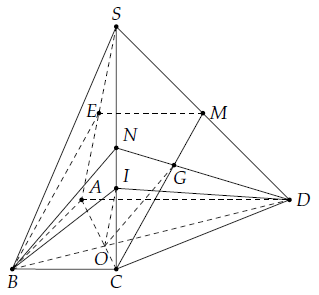
a) Gọi N là trung điểm SC, vì G là trọng tâm ∆SCD
Nên
Ta có: BC // AD
⇒ (Định lí Ta-lét).
∆BND có
⇒ OG // BN (Định lí Ta-lét đảo).
Ta có:
⇒ OG // (SBC).
b) Gọi E là trung điểm của SA, theo tính chất đường trung bình ta có ME // AD và ME = AD.
⇒ Tứ giác MEBC là hình bình hành.
Suy ra: CM // BE.
Ta có:
⇒ CM // (SAB).
c) Ta có: 2SC = 3SI
⇔ 2SI + 2IC = 3SI
⇔ SI = 2IC.
Xét ∆SAC có
⇒ OI // SA (Định lí Ta-lét đảo).
Ta có:
⇒ AB // (BDI).
Câu 19. Cho hình chóp S.ABCD, đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AD, SB.
a) Chứng minh: BD // (MNP).
b) Tìm giao điểm của (MNP) với BC.
c) Tìm giao tuyến của hai mặt phẳng (MNP) và (SBD).
d) Tìm thiết diện của hình chóp với (MNP).
Lời giải
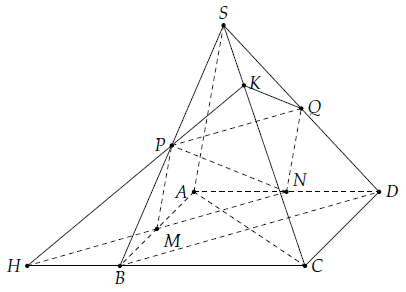
a) ∆ABD có MN là đường trung bình nên MN // BD và MN = BD.
Ta có:
⇒ BD // (MNP).
b) Trong (ABCD), dựng H = MN ∩ BC, ta có:
⇒ H = (MNP) ∩ BC.
c) Gọi ∆ = (MNP) ∩ (SBD), ta có:
Vậy ∆ là đường thẳng qua P và song song với MN.
Gọi Q = ∆ ∩ SD, ta được (MNP) ∩ (SBD) = PQ.
d) Trong (SBC), dựng K = HP∩SC.
Giao tuyến của (MNP) với các mặt phẳng (ABCD), (SAB), (SBC) lần lượt là MN, PM, PK, KQ, QN.
Vậy thiết diện của hình chóp với (MNP) là ngũ giác PMNQK.
Câu 20. Cho tứ diện ABCD. Gọi M là điểm thuộc BC sao cho MC = 2MB. Gọi N, P lần lượt trung điểm của BD và AD.
a) Chứng minh: NP // (ABC).
b) Tìm giao điểm Q của AC với (MNP) và tính . Suy ra thiết diện của hình chóp bị cắt bởi (MNP).
c) Chứng minh: MG // (ABD), với G là trọng tâm của tam giác ACD.
Lời giải
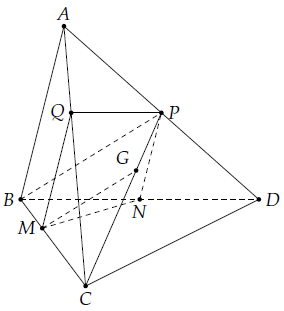
a) ∆ABD có NP là đường trung bình
Nên: NP // AB và NP = AB.
Ta có:
⇒ NP // (ABC).
b) Gọi ∆ = (MNP) ∩ (ABC), ta có:
Vậy ∆ là đường thẳng qua M và song song với AB.
Trong (ABC) dựng Q = ∆ ∩ AC, ta có:
⇒ Q = AC ∩ (MNP).
Ta có:
Xét ∆ABC có QM // AB
⇒
Ta có giao tuyến của (MNP) với các mặt phẳng (ABC), (ACD), (ABD), (BCD) lần lượt là QM, QP, PN, MN.
Vậy thiết diện của hình chóp bị cắt bởi (MNP) là tứ giác MNPQ.
c) Vì G là trọng tâm ∆ACD nên
Xét ∆BCP có
⇒ MG // BP (Định lí Ta-lét đảo).
Ta có:
⇒ MG // (ABD).
Câu 21. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành.
a) Tìm giao tuyến của (SAC) và (SBD); (SAB) và (SCD).
b) Một mặt phẳng qua BC và song song với AD cắt SA tại E (E ≠ S, E ≠ A), cắt SD tại F (F ≠ S, F ≠ D). Tứ giác BEFC là hình gì?
c) Gọi M thuộc đoạn AD sao cho AD = 3AM và G là trọng tâm tam giác SAB, I là trung điểm AB. Đường thẳng qua M và song song AB cắt CI tại N. Chứng minh: NG // (SCD) và MG // (SCD).
Lời giải
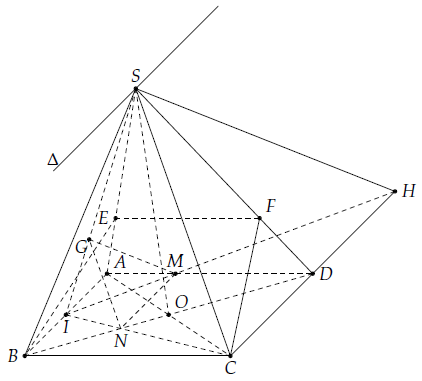
a) Ta có: S ∈ (SAC) ∩ (SBD)
Trong (ABCD), dựng O = AC ∩ BD, ta có:
⇒ O ∈ (SAC) ∩ (SBD).
Vậy: (SAC) ∩ (SBD) = SO.
Gọi ∆ = (SAB) ∩ (SCD), ta có S ∈ ∆.
Ta có:
⇒ ∆ // AB.
Vậy ∆ là đường thẳng qua S và song song với AB.
b) Ta có:
⇒ EF // AD // BC.
Vậy tứ giác BCFE là hình thang.
c) Xét hình thang AICD có MN // AI
⇒ (Định lí Ta-lét).
Vì G là trọng tâm tam giác SAB nên
Xét ∆ISC ta có:
⇒ GN // SC (Định lí Ta-lét đảo).
Ta có:
⇒ NG // (SCD).
Trong (ABCD), dựng H = IM ∩ CD. Vì AI // DM nên ta có:
(Định lí Ta-lét).
Xét ∆ISH ta có:
⇒ GM // SH (Định lí Ta-lét đảo).
Ta có:
⇒ MG // (SCD).
Câu 22. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P lần lượt là trung điểm của SA, BC, CD.
a) Tìm giao tuyến của hai mặt phẳng (SAC) và (SBD).
b) Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD).
c) Tìm giao điểm E của SB và (MNP).
d) Chứng minh: NE // (SAP).
Lời giải
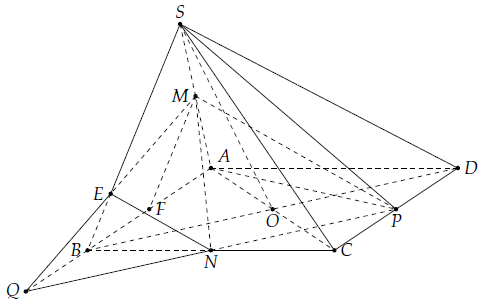
a) Ta có: O = AC ∩ BD
⇒
Do đó: O là điểm chung của hai mặt phẳng (SAC) và (SBD)
Mà: S là điểm chung thứ hai của hai mặt phẳng (SAC) và (SBD)
Nên: SO = (SAC) ∩ (SBD).
b) Ta có:
⇒ (SAB) ∩ (SCD) = Sx // AB và Sx // CD.
c) Gọi Q = NP ∩ AB
⇒ Q là điểm chung của (SAB) và (MNP)
Mà: M là điểm chung thứ hai nên (SAB) ∩ (MNP) = MQ.
Trong mặt phẳng (SAB) gọi E = MQ ∩ SB.
Ta có:
⇒ E = SB ∩ (MNP).
d) Ta có: N là trung điểm của BC và BQ // CP
Nên: BQ = CP và NQ = NP (1).
Gọi F là trung điểm của AB, ta có:
Ta có: M, F là trung điểm của SA và AB
Nên MF là đường trung bình tam giác SAB ⇒ MF // SB.
Trong tam giác QMF có B là trung điểm QF và BE // MF
Nên E là trung điểm MQ (2).
Từ (1) và (2) ta có: EN là đường trung bình tam giác QMP ⇒ EN // MP.
Mặt khác, do MP ⊂ (SAP) nên NE // (SAP).
Câu 23. Cho tứ diện ABCD. Lấy điểm M trên cạnh AB sau cho AM = 2MB. Gọi G là trọng tâm ∆BCD và I là trung điểm CD, H là điểm đối xứng của G qua I.
a) Chứng minh: GD // (MCH).
b) Tìm giao điểm K của MG với (ACD). Tính tỉ số .
Lời giải
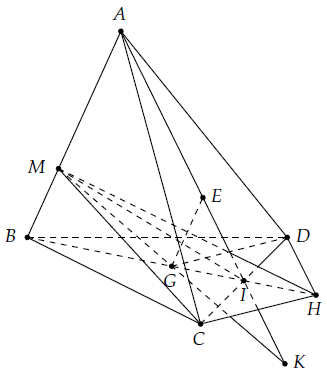
a) Ta có: IC = ID và IG = IH nên GDHC là hình bình hành.
Do đó: GD // CH
Mà CH ⊂ (MCH) nên GD // (MCH).
b) Trong mp(ABI), gọi K = AI ∩ MG, ta có:
⇒ K = MG ∩ (ACD).
Trong mp(ABI), kẻ GE // AB (E ∈ AI).
Xét tam giác ABI, có GE // AB, suy ra:
Xét tam giác AKM, có GE // AM, suy ra:
Câu 24. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, K lần lượt là trung điểm của BC và CD.
a) Tìm giao tuyến của (SIK) và (SAC), (SIK) và (SBD).
b) Gọi M là trung điểm của SB. Chứng minh: SD // (ACM).
c) Tìm giao điểm F của DM và (SIK). Tính tỉ số .
Lời giải
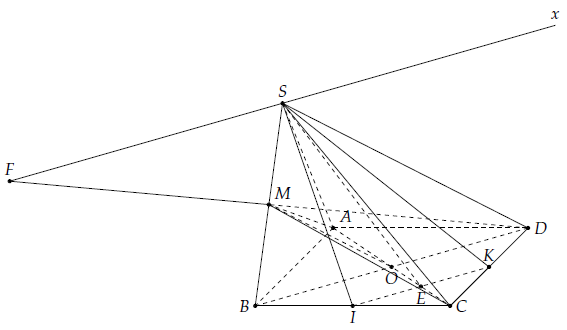
a) Ta có: S ∈ (SIK) ∩ (SAC).
Trong mp(ABCD), gọi E = IK ∩ AC
⇒
⇒ E ∈ (SIK) ∩ (SAC).
Suy ra: SE = (SIK) ∩ (SAC).
Ta có:
⇒ (SIK) ∩ (SBD) = Sx (với Sx // BD // IK)
b) Trong mp(ABCD), gọi O = AC ∩ BD, ta có: SD // MO.
Mà: MO ⊂ (ACM), suy ra SD // (ACM).
c) Trong mp(SBD), gọi F = Sx ∩ DM
⇒
⇒ F = DM ∩ (SIK).
Ta có: SF // BD
⇒
Câu 25. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi G là trọng tâm ∆SAB, trên AD lấy điểm E sao cho AD = 3AE. Gọi M là trung điểm AB.
a) Chứng minh: EG // (SCD).
b) Đường thẳng qua E song song AB cắt MC tại F. Chứng minh: GF // (SCD).
c) Gọi I là điểm thuộc cạnh CD sao cho CI = 2ID. Chứng minh: GO // (SAI).
Lời giải
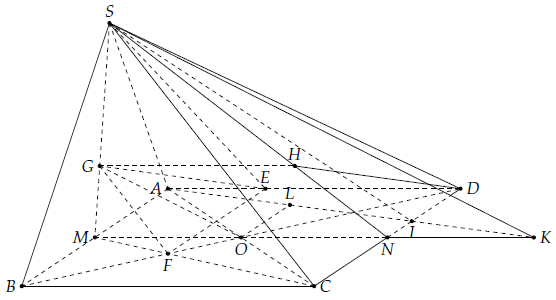
a) Gọi H là trọng tâm tam giác SCD.
Ta có: GH // MN và
Lại có: ED // MN và
Suy ra: GH // ED và GH = ED.
Suy ra GHDE là hình bình hành.
Ta có:
⇒ EG // (SCD).
b) Ta có: MA // EF // CD, suy ra:
Xét tam giác MSC có:
Suy ra: GF // SC.
Mà: SC ⊂ (SCD).
Vậy: GF // (SCD).
c) Trong mp(ABCD), gọi K = AI ∩ MN.
Ta có: SK = (SMN) ∩ (SAI).
Gọi L là trung điểm của AI, ta có OL là đường trung bình của hình thang AMNI, suy ra:
Xét tam giác AKM, có OL // AM, suy ra:
Xét tam giác SMK, có , suy ra GO // SK.
Mà: SK ⊂ (SAI).
Vậy: GO // (SAI).
Câu 26. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm của SC và N là trọng tâm tam giác ABC.
a) Chứng minh: SB // (AMN).
b) Tìm giao tuyến (AMN) và (SAB).
c) Tìm giao điểm I của SD với (AMN). Tính tỉ số .
d) Gọi Q là trung điểm của ID. Chứng minh: QC // (AMN).
Lời giải
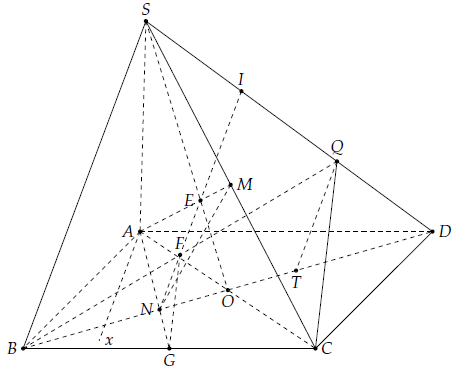
a) Trong mp(ABCD), gọi O = AC ∩ BD.
Trong mp(SAC), gọi E = AM ∩ SO, ta có E là trọng tâm tam giác SAC.
Suy ra:
Ta có: N là trọng tâm tam giác ABC nên .
Xét tam giác OSB có . Suy ra NE // SB.
Mà: NE ⊂ (AMN).
Vậy: SB // (AMN).
b) Ta có:
⇒ (SAB) ∩ (AMN) = Ax (với Ax // SB).
c) Trong mp(SBD), gọi I = NE ∩ SD
⇒
⇒ I = SD ∩ (AMN).
Ta có: NE // SB ⇒ NI // SB
⇒
d) Trong mp(SBD), gọi F = NE ∩ BQ.
Trong mp(ABCD), gọi G = AN ∩ BC, vì N là trọng tâm tam giác ABC nên G là trung điểm của BC.
Ta có: FG = (AMN) ∩ (BQC).
Kẻ QT // FN, (T ∈ BD) (1)
Xét tam giác DNI có QT // NI, suy ra:
Mà nên BN = NT, hay N là trung điểm của BT (2)
Từ (1) và (2), ta có F là trung điểm của BQ.
Do đó: GF là đường trung bình của tam giác BQC.
Suy ra: QC // GF.
Mà: GF ⊂ (AMN).
Vậy: QC // (AMN).
Câu 27. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của BC, CD.
a) Tìm giao tuyến của (SMD) và (SAB).
b) Tìm giao tuyến của (SMN) và (SBD).
c) Gọi H là điểm trên cạnh SA sao cho HA = 2HS. Tìm giao điểm K của MH và (SBD). Tính tỉ số .
d) Gọi G là giao điểm của BN và DM. Chứng minh: HG // (SBC).
Lời giải
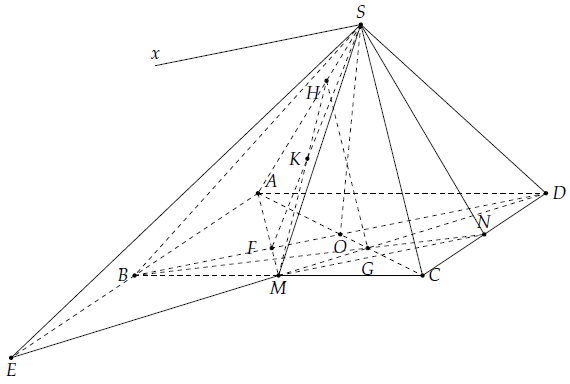
a) Trong mp(ABCD), gọi E = MD ∩ AB
⇒
⇒ E ∈ (SMD) ∩ (SAB).
Mà: S ∈ (SAB) ∩ (SMD)
⇒ SE = (SAB) ∩ (SMD).
b) Ta có:
⇒ (SMN) ∩ (SBD) = Sx // BD // MN.
c) Trong mp(ABCD), gọi F = AM ∩ BD.
Trong mp(SAM), gọi K = MH ∩ SF
⇒
⇒ K = MH ∩ (SBD).
d) Trong tam giác BCD, BN và DM là hai trung tuyến nên G là trọng tâm. Từ đó ta có:
Mặt khác, do HA = 2HS nên:
⇒ HG // SC ⇒ HG // (SBC).
Câu 28. Cho hình chóp S.ABCD có đáy ABCD là hình thang với AD là đáy lớn và AD = 2BC. Gọi O là giao điểm của AC và BD, G là trọng tâm của tam giác SCD.
a) Chứng minh: OG // (SBC).
b) Gọi M là trung điểm của cạnh SD. Chứng minh: CM // (SAB).
c) Giả sử điểm I trên đoạn SC sao cho 2SC = 3SI. Chứng minh: SA // (BID).
d) Xác định giao điểm K của BG và mặt phẳng (SAC). Tính tỉ số .
Lời giải
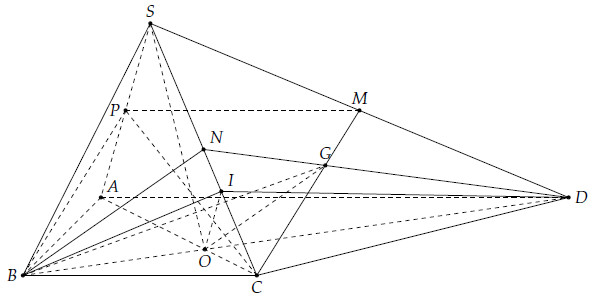
a) Ta có: AD // BC
⇒
Mặt khác, gọi N là trung điểm SC. Vì G là trọng tâm ∆SCD nên
⇒
⇒ OG // BN
⇒ OG // (SBC).
b) Gọi P là trung điểm SA, ta có ngay PM là đường trung bình của ∆
Suy ra: và PM // AD // BC.
Do đó: PMCB là hình bình hành.
Vậy: CM // BP ⇒ CM // (SAB).
c) Ta có: AD // BC
⇒
Mặt khác, vì 2SC = 3SI nên:
⇒ OI // SA ⇒ SA // (BID)
d) Trong mp(BCMP), gọi K = BG ∩ CP
Mà: CP ∈ (SAC) ⇒ K = BG ∩ (SAC).
Ta lại có: CG // BP
⇒
Câu 29. Cho hình chóp S.ABC Gọi M, P, I lần lượt là trung điểm của AB, SC, SB. Một mặt phẳng (α) qua MP và song song với AC và cắt các cạnh SA, BC tại N, Q.
a) Chứng minh BC // (IMP).
b) Xác định thiết diện của (α) với hình chóp. Thiết diện này là hình gì?
c) Tìm giao điểm của đường thẳng CN và mặt phẳng (SMQ).
Lời giải
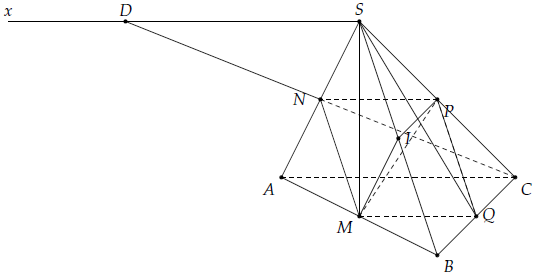
a) Ta có: IP là đường trung bình của tam giác SBC
Nên: IP // BC ⇒ BC // (IMP).
b) Ta có: (α) cắt BC tại Q nên (α) ∩ (SBC) = PQ và (α) ∩ (ABC) = MQ.
Ta lại có: (α) cắt SA tại N nên (α) ∩ (SAB) = MN và (α) ∩ (SAC) = PN.
Vậy thiết diện cần tìm là tứ giác MNPQ.
Mặt khác, do
⇒ (α) ∩ (ABC) = MQ // AC
⇒ Q là trung điểm BC.
Tương tự ta chứng minh được NP // AC và N là trung điểm SA.
Lúc này NP và MQ là đường trung bình tam giác SAC và ABC
Nên NP = MQ = AC và NP // MQ.
Suy ra: MNPQ là hình bình hành.
c) Ta có:
⇒ (SAC) ∩ (SMQ) = Sx // AC.
Trong mp(SAC), gọi D = CN ∩ Sx.
Ta có: D ∈ Sx ⊂ (SMQ) và D ∈ CN
Nên: D = CN ∩ (SMQ).
Câu 30. Cho hình chóp S.ABCD có đáy là một hình tứ giác lồi. Gọi M, N là trung điểm của SC và CD. Gọi (α) là mặt phẳng qua M, N và song song với đường thẳng AC.
a) Tìm giao tuyến của (α) với (ABCD).
b) Tìm giao điểm của SB và (α).
c) Tìm thiết diện của hình chóp cắt bởi mặt phẳng (α).
Lời giải
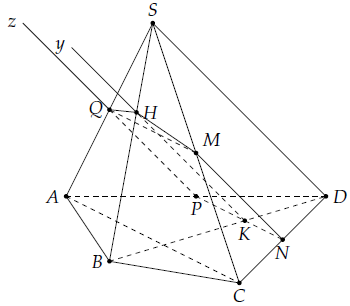
a) Ta có:
⇒ (α) ∩ (ABCD) = Nx // AC.
Gọi P = Nx ∩ AD, ta có: (α) ∩ (ABCD) = NP.
b) Ta có: MN là đường trung bình của tam giác SCD
Nên: SD // MN ⇒ SD // (α).
Gọi K = NP ∩ BD, ta có:
⇒ (α) ∩ (SBD) = Ky // SD.
Gọi H = Ky ∩ SB. Ta có: H ∈ Ky ⊂ (α) và H ∈ SB.
⇒ H = SB ∩ (α).
c) Ta có:
⇒ (α) ∩ (SBD) = Pz // SD. Gọi Q = Pz ∩ SA.
(α) và (SAB) có H, Q là điểm chung nên giao tuyến là QH.
(α) và (SAD) có P, Q là điểm chung nên giao tuyến là PQ.
(α) và (ABCD) có P, N là điểm chung nên giao tuyến là PN.
(α) và (SCD) có M, N là điểm chung nên giao tuyến là MN.
(α) và (SBC) có H, M là điểm chung nên giao tuyến là HM.
Vậy thiết diện cần tìm là ngũ giác MNPQH.
Câu 31. Cho hình chóp S.ABCD có đáy ABCD là hình thang với AB k CD. Gọi M, N, I, lần lượt là trung điểm của AD, BC, SA.
a) Tìm giao tuyến của hai mặt phẳng (IMN) và (SAC); (IMN) và (SAB).
b) Tìm giao điểm của SB và (IMN).
c) Tìm thiết diện của mặt phẳng (IDN) với hình chóp S.ABCD.
Lời giải
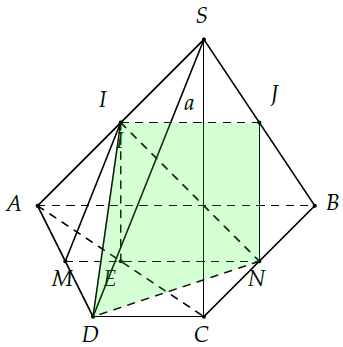
a) Tìm giao tuyến của hai mặt phẳng (IMN) và (SAC); (IMN) và (SAB).
+) Tìm giao tuyến của (IMN) và (SAC).
Ta có: I ∈ (SAC) ∩ (IMN).
Trong (ABCD), gọi E = AC ∩ MN
⇒ E ∈ (SAC) ∩ (IMN).
Vậy: IE = (IMN) ∩ (SAC).
+) Tìm giao tuyến của (IMN) và (SAB).
Ta có: I ∈ (IMN) ∩ (SAB) và MN là đường trung bình của hình thang ABCD
Nên: MN // AB.
Nên giao tuyến của (IMN) và (SAB) là đường thẳng a đi qua I song song với AB.
b) Ta thấy: SB ⊂ (SAB) và a = (IMN) ∩ (SAB).
Gọi J = SB ∩ a, vậy J = SB ∩ (IMN).
c) Ta thấy:
IJ = (SAB) ∩ (IDN),
ID = (SAD) ∩ (IDN),
DN = (ABCD) ∩ (IDN),
NJ = (SBC) ∩ (IDN).
Vậy thiết diện của (IDN) và hình chóp S.ABCD là tứ giác IJND.
Câu 32. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi G là trọng tâm ∆SAB; N là một điểm thuộc đoạn AC sao cho ; I là trung điểm của AB.
a) Chứng minh: OI // (SAD) và GN // SD.
b) Gọi (α) là mặt phẳng đi qua O, song song với SA và BC. Mặt phẳng (α) cắt SB, SC lần lượt tại L và K. Xác định thiết diện cắt bởi mặt phẳng (α) với hình chóp.
Lời giải
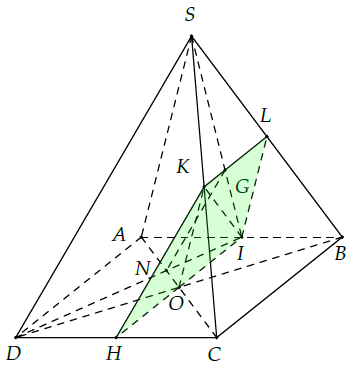
a) Chứng minh OI // (SAD) và GN // SD.
+) Chứng minh: OI // (SAD).
Ta có: OI // BC (OI là đường trung bình trong ∆ABC)
Nên: OI // AD (vì AD // BC)
Mà: AD ⊂ (SAD) suy ra OI // (SAD).
+) Chứng minh: GN // SD.
Do suy ra N là trọng tâm ∆ABD.
Từ đó ta có:
b) Xác định giao điểm L = SB ∩ (α).
Ta thấy: (α) là (KIH) với H, K lần lượt là trung điểm CD, SC.
Ta thấy: SB ⊂ (SBC), K = (α) ∩ (SBC) và IH // BC
Nên giao tuyến của (α) và (SBC) là đường thẳng d đi qua K song song với BC.
Khi đó: L = d ∩ SB suy ra L là trung điểm SB.
Ta thấy:
(α) ∩ (ABCD) = HI,
(α) ∩ (SBC) = KL,
(α) ∩ (SAB) = LI.
Vậy thiết diện của (α) với hình chóp là hình thang LKHI.
Câu 33. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi H, K lần lượt là trung điểm các cạnh SA, SB và M là điểm thuộc cạnh CD, (M khác C và D).
a) Tìm giao tuyến của (KAM) và (SBC), (SBC) và (SAD).
b) Tìm thiết diện tạo bởi (HKO) với hình chóp S.ABCD. Thiết diện là hình gì?
c) Gọi L là trung điểm đoạn HK. Tìm I = OL ∩ (SBC). Chứng minh: SI // BC.
Lời giải
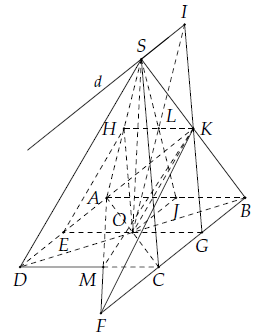
a) Tìm giao tuyến của (KAM) và (SBC), (SBC) và (SAD).
+) Tìm giao tuyến của (KAM) và (SBC).
Ta có: K ∈ (KAM) ∩ (SBC).
Trong (ABCD), gọi F = AM ∩ BC
Nên: F ∈ (KAM) ∩ (SBC).
Suy ra: KF = (KAM) ∩ (SBC).
+) Tìm giao tuyến của (SBC) và (SAD).
Ta thấy: S ∈ (SBC) ∩ (SAD)
Mà: BC // AD
Nên giao tuyến của (SBC) và (SAD) là đường thẳng d đi qua S song song với AD và BC.
b) Tìm thiết diện tạo bởi (HKO) với hình chóp S.ABCD. Thiết diện là hình gì?
Ta thấy (HKO) và (ABCD) chứa có chung điểm O và lần lượt chứa HK và AB song song với nhau. Nên giao tuyến là đường thẳng a đi qua O song song với AB cắt AD và BC lần lượt tại E và G. Ta thấy:
(HKO) ∩ (ABCD) = EG,
(HKO) ∩ (SAD) = HE,
(HKO) ∩ (SAB) = HK,
(HKO) ∩ (SBC) = KG.
Vậy: thiết diện của (HKO) và hình chóp là hình thang HKGE
Do HK // AB mà AB // EG nên HK // EG.
c) Tìm I = OL ∩ (SBC). Chứng minh: SI // BC.
Trong (HKGE), gọi I = OL ∩ GK
Mà GK ⊂ (SBC) ⇒ I ∈ OL ∩ (SBC).
Trong (SAB), gọi J = SL ∩ AB
Khi đó: L là trung điểm của AB do HK // AB.
Xét (SJO) và (SBC), ta thấy có S là điểm chung và OJ // BC
Nên giao tuyến là đường thẳng d đi qua S và song song với BC.
Mặt khác: I ∈ (SJO) ∩ (SBC) nên SI ≡ d.
Vậy: SI // BC.
Câu 34. Cho tứ diện ABCD, có M, N lần lượt là trung điểm của AB, BC và G là trọng tâm của tam giác ACD.
a) Tìm giao điểm E của MG và (BCD).
b) Tìm d = (MNG) ∩ (BCD). Giả sử d ∩ CD = P. Chứng minh: GP // (ABC).
c) Gọi (α) là mặt phẳng chứa MN và song song với AD. Tìm thiết diện của (α) với tứ diện.
Lời giải
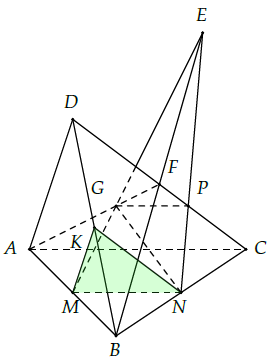
a) Ta thấy: (ABF) chứa MG với F là trung điểm của DC
Và: BF = (ABF) ∩ (BCD).
Gọi E = MG ∩ BF ⇒ E = MG ∩ (BCD).
b) Ta có:
N ∈ (BCD) ∩ (MNG);
E ∈ MG ⊂ (MNG);
E ∈ BF ⊂ (BCD).
Suy ra: d ≡ NE = (MNG) ∩ (BCD).
Ta thấy:
(ABC) ∩ (EMN) = MN,
(DAC) ∩ (ABC) = AC,
(EMN) ∩ (DAC) = GP.
Mà: MN // AC nên GP // AC ⇒ GP // (ABC).
c) Gọi K là trung điểm của BD.
Do (α) chứa MN và song song với AD nên (α) đi qua K.
Ta thấy:
(α) ∩ (ABD) = MK,
(α) ∩ (ABC) = MN,
(α) ∩ (BCD) = KN.
Vậy thiết diện của (α) và hình chóp là tam giác MNK.
Câu 35. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Điểm M thuộc cạnh SA thỏa mãn 3MA = 2MS. Hai điểm E và F lần lượt là trung điểm của AB và BC.
a) Xác định giao tuyến của hai mặt phẳng (MEF) và (SAC).
b) Xác định giao điểm K của mặt phẳng (MEF) với cạnh SD. Tính tỉ số .
c) Tìm giao điểm I của MF với (SBD). Tính tỉ số .
d) Tìm thiết diện tạo bởi mặt phẳng (MEF) với hình chóp S.ABCD.
Lời giải
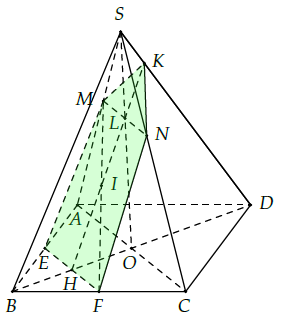
a) Ta thấy: M ∈ (MEF) ∩ (SAC)
Và: EF // AC với EF ⊂ (MEF), AC // (SAC)
Nên giao tuyến của (MEF) và (SAC) là đường thẳng d đi qua M song song với AC.
b) Ta thấy: SD ⊂ (SBD)
Gọi H = EF ∩ BD, O = AC ∩ BD, L = d ∩ SO.
Khi đó: HL = (MEF) ∩ (SBD)
Gọi K = HL ∩ SD ⇒ K = SD ∩ (MEF).
Do ML // AC nên
Xét tam giác SOD, trong (SBD) vì K, L, H thẳng hàng nên theo định lí Menelaus ta có:
c) Trong (MEF), gọi I = HL ∩ MF
Mà: HL ⊂ (SBD) ⇒ I = MF ∩ (SBD).
Do ML // AC và EF // AC nên ML // EF.
Từ đó ta suy ra:
d) Tìm thiết diện tạo bởi mặt phẳng (MEF) với hình chóp S.ABCD.
Gọi N = ML ∩ SC. Ta thấy:
(MEF) ∩ (SAB) = EM,
(MEF) ∩ (ABCD) = EF,
(MEF) ∩ (SAD) = MK,
(MEF) ∩ (SCD) = KN,
(MEF) ∩ (SBC) = NF.
Vậy thiết diện của (MEF) với hình chóp là ngũ giác EMKNF.
Câu 36. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N là trung điểm của SA, SD.
a) Xác định giao điểm của NC và (OMD).
b) Xác định thiết diện của hình chóp với mặt phẳng (P) qua MN và song song với SC.
Lời giải
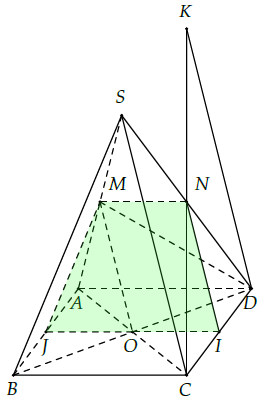
a) Xác định giao điểm của NC và (OMD).
Ta thấy: CN ⊂ (SCD), OM // SC
Mà: OM ⊂ (OMD), SC ⊂ (SCD)
Và O ∈ (OMD) ∩ (SCD)
Nên giao tuyến của (OMD) và (SCD) là đường thẳng d đi qua D và song song với OM, SC.
Gọi K = d ∩ NC ⇒ K = NC ∩ (OMD).
b) Xác định thiết diện của hình chóp với mặt phẳng (P) qua MN và song song với SC.
Ta thấy: (P) ≡ (OMN).
Xác định giao tuyến của (OMN) và (SCD).
Ta thấy: N ∈ (OMN) ∩ (SCD) và OM // SC
Nên giao tuyến của (OMN) và (SCD) là đường thẳng đi qua N song song với SC cắt CD tại I là trung điểm CD.
Gọi J = OI ∩ AB. Ta thấy:
(OMN) ∩ (SAB) = JM,
(OMN) ∩ (SAD) = MN,
(OMN) ∩ (SCD) = IN,
(OMN) ∩ (ABCD).
Vậy thiết diện của mặt phẳng (P) với hình chóp là hình thang MNIJ.
Câu 37. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm của SC, (P) là mặt phẳng qua AM và song song với BD.
a) Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng (P).
b) Gọi E, F lần lượt là giao điểm của (P) với cạnh SB và SD. Hãy tìm tỉ số diện tích của tam giác SME với diện tích tam giác SBC và tỉ số diện tích của tam giác SMF và diện tích tam giác SCD.
c) Gọi K là giao điểm của ME và CB, J là giao điểm của MF và CD. Chứng minh ba điểm K, A, J nằm trên một đường thẳng song song với EF và tìm tỉ số .
Lời giải
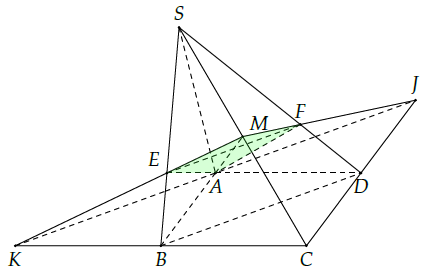
a) Trong (ABCD) qua A kẻ đường thẳng song song BD cắt BC và CD lần lượt tại K và J.
Khi đó: (P) ≡ (MK J).
Gọi E = MK ∩ SB, F = CD ∩ SD.
Khi đó, ta thấy:
(P) ∩ (SAB) = EA,
(P) ∩ (SBC) = EM,
(P) ∩ (SCD) = MF,
(P) ∩ (SAD) = AF.
Vậy thiết diện của (P) với hình chóp là tứ giác AEMF.
b) Ta có:
(Vì E là giao điểm của hai đường trung tuyến KM và SB nên E là trọng tâm của tam giác SCK)
Tương tự ta có:
(Vì F là giao điểm của hai đường trung tuyến JM và SD nên F là trọng tâm của tam giác SCJ)
c) Ta có:
Câu 38. Cho hình chóp S.ABCD có G là trọng tâm ∆ABC. Gọi M, N, P, Q, R, H lần lượt là trung điểm của SA, SC, CB, BA, QN, AG.
a) Chứng minh rằng: S, R, G thẳng hàng và SG = 2MH = 4RG.
b) Gọi G’ là trọng tâm ∆ Chứng minh rằng: GG’ // (SAB) và GG’ // (SAC).
Lời giải
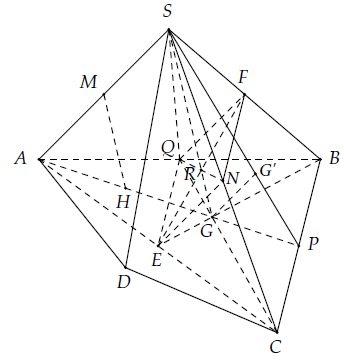
a) Gọi E, F lần lượt là trung điểm của AC và SB
Khi đó ta có: QENF là hình bình hành
Nên R là trung điểm của EF. Ta thấy:
S ∈ (SQC) ∩ (SEB),
G ∈ (SQC) ∩ (SEB),
R ∈ (SQC) ∩ (SEB)
Suy ra: S, R, G thẳng hàng.
Vì M, H lần lượt là trung điểm của SA, AG nên SG = 2MH.
Xét ∆SGB vì E, R, F thẳng hàng nên theo định lí Menelaus ta có:
b) Xét ∆SAP có
⇒ GG’ // SA
Mà: SA ⊂ (SAB) và SA ⊂ (SAC)
Nên suy ra: GG’ // (SAB), GG’ // (SAC).
Bạn đang xem bài viết Lý thuyết & bài tập xem thêm các bài viết khác về chủ đề Toán lớp 11. Chúc bạn 1 ngày vui vẻ!