Toán lớp 11: Hai đường thẳng vuông góc mới nhất 2023

trong văn bản, học ngôn ngữ Toàn bộ lý thuyết và 3 dạng bài tập cơ bản của chuyên đề sẽ được tổng hợp hai hàng dọc trong không gian.

Lý thuyết về hai đường thẳng vuông góc trong không gian

1. Tích vô hướng của hai vectơ trong không gian

trong không gian, cho Và là hai vectơ khác vectơ không.Lấy điểm A bất kỳ, gọi hai điểm B, C sao cho .sau đó tôi gọi là góc giữa hai vectơ Và biểu tượng .

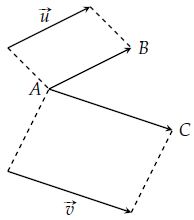
trong không gian, cho Và là hai vectơ khác vectơ không.tích vô hướng của hai vectơ Và là một số biểu thị như và được tính theo công thức

ở trường hoặc chúng ta đồng ý .

2. Góc giữa hai đường thẳng

định nghĩa 1

véc tơ Trừ véc tơ – nếu giá của véc tơ không gọi là véc tơ chỉ phương của đường thẳng d Song song hoặc trùng với đường thẳng d.

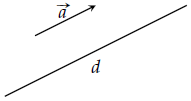
chú ý:

1) nếu là vectơ chỉ phương của đường thẳng d thì vectơ trong đó k ≠ 0 cũng là vectơ chỉ phương của đường thẳng d.

2) Nếu biết điểm A thuộc d và biết vectơ chỉ phương . thì đường thẳng d trong không gian hoàn toàn xác định nó là.

3) Hai đường thẳng song song khi và chỉ khi chúng là hai đường thẳng khác nhau và có hai vectơ chỉ phương cùng phương.

định nghĩa 2

Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a’ và b’ lần lượt đi qua một điểm và song song với a và b.

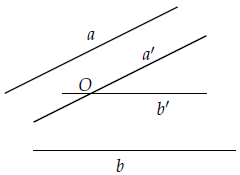
chú ý:

1) Để xác định góc giữa hai đường thẳng a và b, ta có thể lấy một điểm O nằm trên một trong hai đường thẳng đó và kẻ một đường thẳng qua O và song song với đường thẳng kia.

2) nếu Và lần lượt là các vectơ chỉ phương của a và b, và Nếu 0° ≤ α ≤ 90° thì góc giữa hai đường thẳng a và b bằng α; nếu 90° < α ≤ 180° thì góc giữa hai đường thẳng a và b bằng α; nếu 90° < α ≤ 180° thì góc giữa hai đường thẳng a và b bằng α.

3) Nếu a và b là hai đường thẳng song song hoặc trùng nhau thì góc giữa chúng bằng 0°.

3. Hai đường thẳng vuông góc với nhau

Hai đường thẳng được gọi là vuông góc nếu góc giữa chúng bằng 90°.gọi lần lượt là vectơ chỉ phương của các đường thẳng a và b. Ta nói a vuông góc với b trong không gian khi thỏa mãn các điều kiện sau: .

Dạng 1. Xác định góc giữa hai vectơ

Giải pháp

Chúng ta xác định một điểm cho trước trên đồ thị là gốc tọa độ và di chuyển vectơ để tính góc từ gốc tọa độ đó.

bài tập áp dụng

Câu hỏi 1. Cho tứ diện đều ABCD có H là trung điểm của cạnh AB. Tính góc giữa các cặp vectơ sau:

Đầu tiên) Và

2) Và

Trả lời

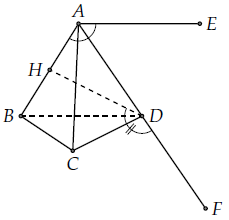
1) xây dựng . Chúng ta có:

2) Xây dựng . Chúng ta có:

chương 2. Cho tứ diện SABC có các cạnh bên SA, SB, SC và SA = SB = SC = a. Gọi M là trung điểm của BC.Tính góc giữa hai vectơ Và .

Trả lời

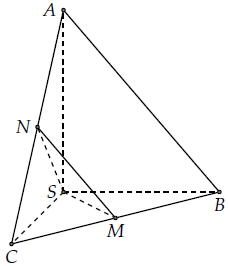
Gọi α là góc giữa hai vectơ Và Chúng ta có:

có:

Mặt khác chúng ta có:

Vì thế:

Cách khác: Gọi N là trung điểm của AC, ta dễ dàng chứng minh được ΔSMN đều.

có

Dạng 2. Xác định góc giữa hai đường thẳng trong không gian

Giải pháp

Chúng ta thường có hai cách tiếp cận để giải các bài toán như vậy.

+) Cách 1: Sử dụng định nghĩa góc giữa hai đường thẳng, kết hợp với sử dụng hệ thức lượng giác (định luật cosin, công thức trung tuyến).

+) Cách 2: Sử dụng tích bằng không của hai vectơ.

bài tập áp dụng

Câu hỏi 1. Cho hình lập phương ABCD.A’B’C’D’ có cạnh a.Tính góc giữa các cặp đường thẳng sau

1) AB và A’D’

2) AD và A’C’

3) BC’ và B’D’

Trả lời

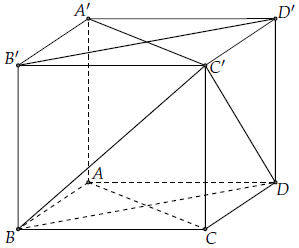
1) Ta có A’D’ // AD nên

2) Ta có A’C’ // AC nên

3) Ta có B’D’ // BD nên

Chúng ta có Vậy BDC’ đều, suy ra

Vậy (BC’, B’D’) = 60°.

chương 2. Cho hình chóp S.ABC có SA = SB = SC = AB = AC = BC = 2a. Tính góc giữa hai đường thẳng AC và SB.

Trả lời

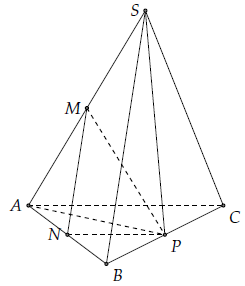
Ta có SAB và SAC là các tam giác đều và ABC và SBC là các tam giác vuông có cạnh huyền BC.

Gọi M, N, P lần lượt là trung điểm của SA, AB, BC.

Ta có MN // SB, NP // AC nên (AC, SB) = (NP, MN).

Vậy ΔSAP vuông góc với P

⇒

Vậy ΔMNP chẵn

⇒

cách khác:

Mục 3. Cho đáy ABC của hình chóp S.ABC là tam giác đều cạnh 2a, tam giác SBC vuông tại S, SA = 2a.

1) Tính góc giữa hai đường thẳng SB và AC.

2) Gọi G là trọng tâm tam giác SBC. Tính góc tạo bởi AG và SC.

Trả lời.

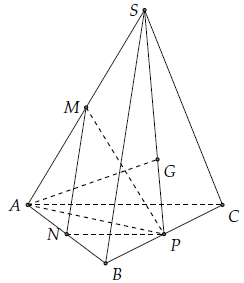
1) Gọi M, N, P là trung điểm của SA, AB, BC

Ta có MN // SB, NP // AC nên (SB, AC) = (MN, NP).

∆ABC đều

∆SBC vuông góc với S nên

Mặt khác có Vậy ΔSAP là P bình phương.

2) Ta có:

có

Phần 4. Cho tứ diện đều ABCD có cạnh a. Gọi M là một điểm trên cạnh AB sao cho BM = 3AM. Tính góc tạo bởi hai đường thẳng CM và BD.

Trả lời.

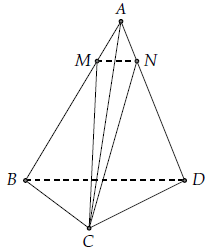
Vẽ MN // BD, N ∈ AD, ta có (CM, BD) = (CM, MN).

Vì ABCD là tứ diện đều nên có:

Câu 5. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, các tam giác SAB và SAD vuông góc tại A.Một người nổi tiếng gọi M là trung điểm của cạnh SB.

1) Tính góc tạo bởi hai vectơ Và .

2) Tính góc tạo bởi hai đường thẳng AM và SC.

Trả lời.

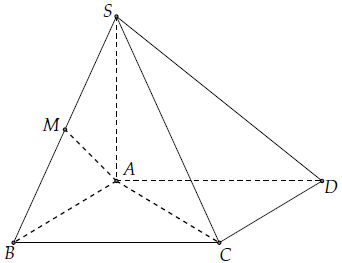
1) là:

Vì ABCD là hình vuông nên

Vì thế:

2) SAB vuông A nên

có:

nên:

Mục 6. Cho hình lập phương ABCD.A’B’C’D’ có cạnh a, gọi M là trung điểm của AB, N là điểm thuộc cạnh B’C’ sao cho B’N = 2C’N. Tính cosin của góc tạo bởi hai đường thẳng DM và AN.

Trả lời.

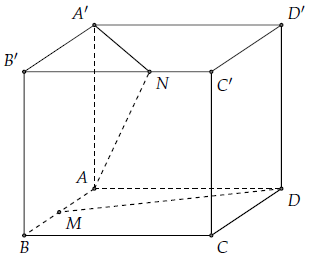
Chúng ta có:

Vì thế nên:

có:

Dạng 3. Sử dụng tính chất vuông góc trong mặt phẳng.

Giải pháp

Để chứng minh hai đường thẳng Δ và Δ’ vuông góc với nhau ta có thể sử dụng phép tính vuông góc trong mặt phẳng, cụ thể:

+) Tam giác ABC vuông góc với A khi và chỉ khi

+) Tam giác ABC vuông góc với A khi và chỉ khi AB² + dòng điện xoay chiều² = TCN^2.

+) Tam giác ABC vuông tại A khi và chỉ khi trung tuyến của A bằng nửa cạnh BC.

+) Nếu tam giác ABC cân tại A thì trung tuyến của A cũng chính là đường cao của tam giác.

Ngoài ra, chúng ta sử dụng tính chất sau: Nếu d ⊥ Δ và Δ’ // d thì Δ’ cũng vuông góc với đường thẳng Δ.

bài tập áp dụng

Câu hỏi 1. Cho tứ diện ABCD có AB = AC = AD, . Gọi M, N lần lượt là trung điểm của AB, CD, chứng minh MN là đường vuông góc chung của các đường thẳng AB, CD.

Trả lời.

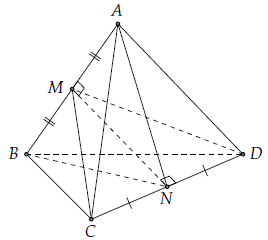
Suy ra từ giả thiết các tam giác ABC, ABD đều nên DM = CM nên ΔMCD cân tại M.

Từ đó suy ra MN ⊥ CD.

Ngược lại ΔBCD = ΔACD nên BN = AN nên ΔNAB cân bằng tại N.

Từ đó suy ra NM⊥AB.

Vậy MN là đường vuông góc chung của AB và CD.

chương 2. Cho hình chóp S.ABC có . Gọi H là trung điểm của AC. chứng minh:

1) SH ⊥ AC.

2)AB⊥BC.

Trả lời

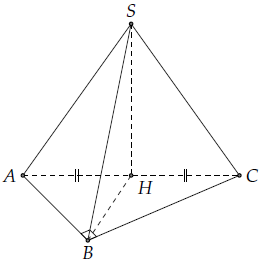
1) Vì tam giác SAC cân tại S và H là trung điểm của AC nên SH⊥AC.

2) Vì SA = SB = a và Vậy ΔSAB là số chẵn.

Từ đó ta thấy: AB = a (1)

Áp dụng định lý hàm số cosin cho tam giác SAC ta có:

Áp Dụng Định Lý Pitago Cho Tam Giác SBC

tôi có BC² = SB² + SC² = 2a² (3)

AC được suy ra từ (1), (2), (3)² = AB² + TCN² ⇒ AB ⊥ BC.

Mục 3. Cho hình chóp S.ABCD SA = x, các cạnh còn lại đều bằng 1. Chứng minh rằng SA ⊥ SC.

Trả lời

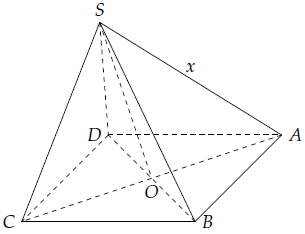
Ta có hình thoi ABCD, gọi O là giao điểm của AC và BD

Vậy O là trung điểm của AC và BD.

Xét các tam giác SBD và CBD ta có:

suy ra từ đây

Do đó tam giác SAC vuông góc với S hay SA ⊥ SC .

Phần 4. Cho đáy ABCD của hình chóp S.ABCD là hình vuông tâm O, SA = SB = SC = SD. Chứng minh rằng SO ⊥ AB và SO ⊥ AD.

Trả lời.

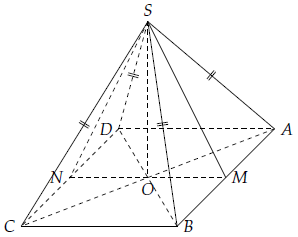
Gọi M, N lần lượt là trung điểm của AB, CD.

Vì ΔSAB = ΔSCD nên suy ra SM = SN.

Xét tam giác cân SMN có O là trung điểm của MN, suy ra SO ⊥ MN.

Khác AD // MN nên AD ⊥ SO.

Tương tự, ta chứng minh được AB⊥SO.

Câu 5. Gọi M, N của hình lập phương ABCD.A’B’C’D’ lần lượt là trung điểm của BC và C’D’. Chứng minh rằng AM ⊥ B’N.

Trả lời.

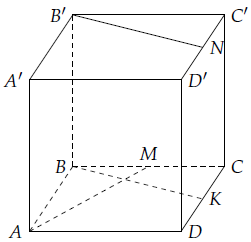
Gọi K là trung điểm của CD thì BK // B’N. Ta sẽ chứng minh rằng BK ⊥ AM.

Gọi I là giao điểm của BK và AM. Vì ΔABM = ΔBCK nên:

Vậy BK ⊥ AM tại I.

Mục 6. Xét hình chóp S.ABCD có đáy là hình vuông có các cạnh bằng a. Gọi M, N lần lượt là trung điểm của AD, SD, chứng minh MN⊥SC.

Trả lời.

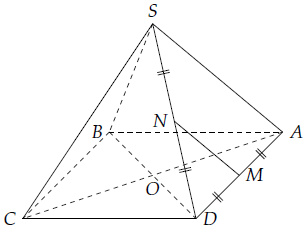
Theo giả thiết ta có:

Ngược lại MN // SA ⇒ MN ⊥ SC.

Mục 7. Cho hình chóp S.ABCD có đáy là hình vuông có cạnh bằng 2a, tam giác đều SAB và . Gọi H, K lần lượt là trung điểm của AB, CD. Chứng minh rằng SH⊥AK.

Trả lời.

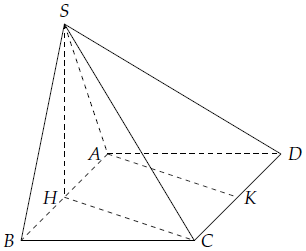
Ta có: AK // HC nên chỉ cần chứng minh SH ⊥ HC.

Vì ΔSAB cạnh 2a nên:

Ta có: HC² = HB² + TCN² = một² + 4a² = 5a².

Từ đó suy ra: SH² + HC² = 3a² + 5a² = 8a² = SC².

Theo định lý Pitago, ta có SH ⊥ HC.

Mục 8. Cho tứ diện ABCD có AB = x, các cạnh còn lại có độ dài a. K là trung điểm của AB, I là điểm bất kì trên cạnh CD, chứng minh rằng IK ⊥ AB.

Trả lời.

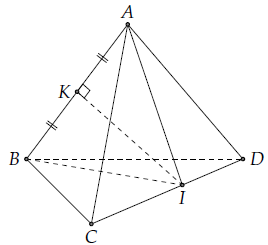
Xét các tam giác ACI và BCI, ta có:

Từ đó suy ra: ΔACI = ΔBCI ⇒ IB = IC.

Xét tam giác cân IAB, ta có K là trung điểm của AB nên IK⊥AB.

Mục 9. Cho hình chóp S.ABCD có đáy ABCD là hình thang thẳng tại A và B, AD = 2a, AB = BC = a. SA ⊥ AD và SA ⊥ AC. Chứng minh rằng SC⊥DC.

Trả lời.

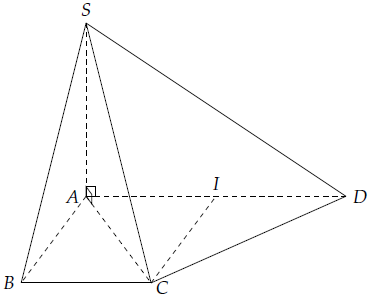
Gọi I là trung điểm của AD ⇒ ABCI là hình vuông cạnh a nên ΔCID vuông góc với I. Từ đây chúng ta có đĩa CD² = 2a ². (Đầu tiên)

Áp dụng định lí Pitago cho các tam giác SAC, SAD ta có:

SD² = SA² + quảng cáo² = SA² + 4a² (2)

SC² = SA² + dòng điện xoay chiều² = SA² + 2a² (3)

Từ (1), (2), (3) suy ra

SD² = SC² + đĩa² ⇒ SC ⊥ CD.

Dạng 4. Hai đường thẳng song song thì vuông góc với đường thẳng thứ ba

Giải pháp

Để chứng minh đường thẳng a ⊥ b, ta chứng minh a // a’, trong đó a’ ⊥ b.

bài tập áp dụng

Câu hỏi 1. Cho hình chóp S.ABC có AB = AC. Gọi M, N, P lần lượt là trung điểm của các cạnh BC, SB, SC. Chứng minh rằng AM vuông góc với NP.

Trả lời

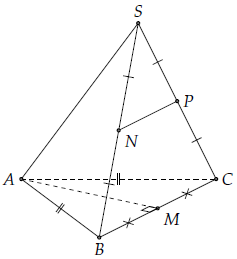
Vì N, P lần lượt là trung điểm của các cạnh SB, SC mà NP là trung điểm của tam giác SBC nên NP // BC (1)

Mặt khác, do tam giác ABC cân tại A nên đường trung trực AM BC (2)

AM⊥NP được suy ra từ (1) và (2).

chương 2. Cho lăng trụ đứng tam giác ABC.A’B’C’ có đáy là tam giác đều. Gọi M là trung điểm của cạnh BC. Chứng minh rằng AM vuông góc với B’C’.

Trả lời

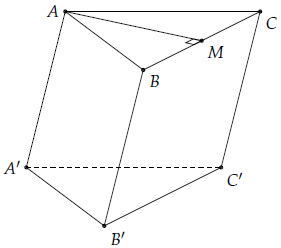
Vì tứ giác BB’C’C là hình bình hành nên BC // B’C’ (1)

Mặt khác, do ABC là tam giác đều nên AM BC (2)

Từ (1) và (2) suy ra AM⊥B’C’.

Mục 3. Cho hình lập phương ABCD.A’B’C’D’ hình lập phương ABCD.A’B’C’D’ cạnh a. Điểm M, N lần lượt là trung điểm của cạnh AB, BC. Lấy điểm P trên cạnh B’C’ sao cho C’P = x (0 < x < a). Lấy điểm Q trên cạnh C'D' sao cho C'Q = x. Chứng minh MN vuông góc với PQ.

Trả lời.

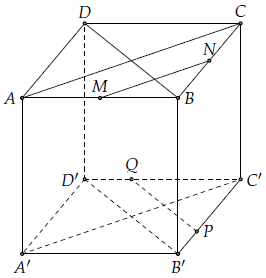
Vì tứ giác BB’D’D là hình chữ nhật nên BD // B’D’ (1)

Vì ABCD là hình vuông nên suy ra BD AC (2)

Từ (1) (2) suy ra B’D’⊥ AC (3)

Theo đề bài, MN là trung điểm của tam giác ABC, suy ra MN // AC (4)

Mặt khác, chúng ta có Suy ra PQ // B’D’ (5)

Từ (3), (4), (5) ta có MN ⊥ PQ.

Phần 4. Cho lăng trụ đứng ABC.A’B’C’. Gọi G, G’ lần lượt là trọng tâm hai đáy. Chứng minh rằng GG’ vuông góc với BC.

Trả lời.

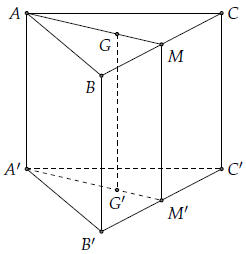
Dễ dàng chứng minh được GG’//MM’ và MM’⊥BC.

Nó có thể được nhìn thấy từ điều này.

Câu 5. Cho tứ diện đều ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, CD, AD, AC. Chứng minh MN vuông góc với PQ.

Trả lời.

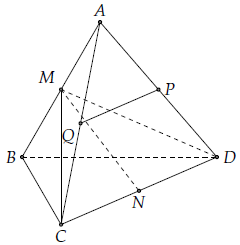
Giả sử chúng ta có ABC = ΔABD

Từ đó ta có MC = MD suy ra MCD cân tại M suy ra MN ⊥ CD (1)

Cũng giả sử PQ là đường trung bình của tam giác ACD suy ra PQ // CD (2)

Từ (1)(2) suy ra điều phải chứng minh.

Mục 6. Cho tứ diện ABCD, AB = CD = 2a (a > 0). Gọi M, N lần lượt là trung điểm của cạnh BC, AD.Tôi biết . Chứng minh rằng AB vuông góc với CD.

Trả lời.

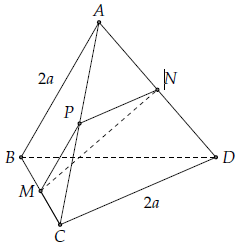
Gọi P là trung điểm của AC.

Theo tính chất của đường trung bình động, ta có Và

^{từ đó chúng ta có ông} 2^{+ NP} 2^{= 2a} 2^{= Minnesota}

2

Do đó, tam giác MNP nằm bên phải P suy ra MP ⊥ NP. (**)

từ (**) Ta có AB ⊥ CD.

Mục 7.

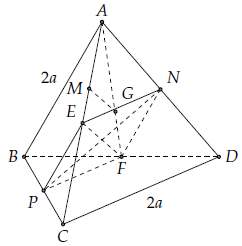
Cho tứ diện ABCD có AB = CD. Gọi G là trọng tâm của tam giác ABD, M thuộc cạnh AC sao cho AC=3AM, N và P lần lượt là trung điểm của cạnh AD và BC. Chứng minh MG vuông góc với NP.

Trả lời. Gọi E, F lần lượt là trung điểm của AC, BD.

Chúng ta có

suy ra MG // EF (1)

Mặt khác, theo tính chất đường trung bình động, ta có