Bạn đang xem bài viết Phân dạng bài tập có lời giải. Hi vọng sẽ là đáp án bạn ưng ý. Cùng theo dõi nhé!
Ở các cấp học dưới, phương pháp quy nạp toán học thường được giới thiệu khi giải các bài toán cực khó. Tuy nhiên, trong chương trình toán 11 chúng ta sẽ tìm hiểu kĩ hơn phương pháp này và vận dụng giải các bài toán từ cơ bản đến nâng cao.
Lý thuyết phương pháp quy nạp toán học
Bài toán
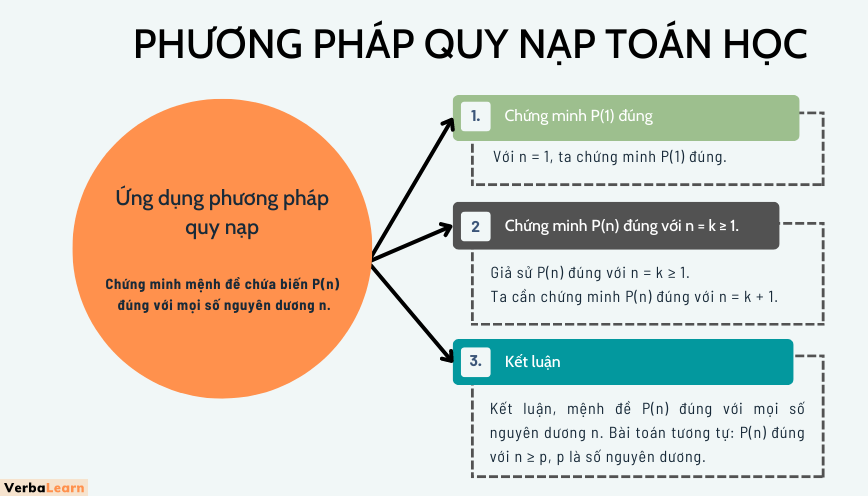
Chứng minh mệnh đề chứa biến P(n) đúng với mọi số nguyên dương n.
Phương pháp chứng minh
+) Bước 1. Với n = 1, ta chứng minh P(1) đúng.
+) Bước 2. Giả sử P(n) đúng với n = k ≥ 1.
Ta cần chứng minh P(n) đúng với n = k + 1.
Kết luận, mệnh đề P(n) đúng với mọi số nguyên dương n.
Lưu ý
Để chứng minh mệnh đề chứa biến P(n) đúng với n ≥ p, p là số nguyên dương. Ta cũng làm các bước tương tự như trên.
+) Bước 1. Với n = p, ta chứng minh P(p) đúng.
+) Giả sử P(n) đúng với n = k ≥ p.
Ta cần chứng minh P(n) đúng với n = k + 1.
Kết luận, mệnh đề P(n) đúng với mọi số nguyên dương n.
Dạng 1. Chứng minh mệnh đề P(n) đúng với mọi số tự nhiên n
Thực hiện theo các bước đã nêu ở phần tóm tắt lí thuyết.
Câu 1. Chứng minh rằng với mọi số tự nhiên n ≥ 1, ta có:
a)
b)
Lời giải
a) Đặt
Với n = 1 thì
Vậy (1) đúng với n = 1.
Giả sử (1) đúng với n = k ≥ 1, k ∈ ℕ, tức là ta có:
Ta cần chứng minh (1) cũng đúng với n = k + 1, tức là cần chứng minh:
Thật vậy, ta có:
Vậy (1) đúng với n = k + 1.
Do đó, với mọi số tự nhiên n ≥ 1.
b) Đặt:
Với n = 1 thì
Vậy (1) đúng với n = 1.
Giả sử (1) đúng với n = k ≥ 1, k ∈ ℕ, tức là ta có:
Ta cần chứng minh (1) cũng đúng với n = k + 1, tức là cần chứng minh:
Thật vậy, ta có:
Vậy (1) đúng với n = k + 1.
Do đó, với mọi số tự nhiên n ≥ 1.
Nhận xét. Với mọi số tự nhiên n ≥ 1, ta có:
Câu 2. Chứng minh rằng với mọi số tự nhiên n ≥ 1, ta luôn có :
a) un = n3 + 3n2 + 5n chia hết cho 3.
b) un = 9n – 1 chia hết cho 8.
Lời giải
a) Với n = 1, ta có: u1 = 13 + 3.12 + 5.1 = 9 chia hết cho 3.
Vậy mệnh đề đúng với n = 1.
Giả sử mệnh đề đúng với n = k ≥ 1, k ∈ ℕ, tức là uk = k3 + 3k2 + 5k chia hết cho 3.
Ta cần chứng minh uk+1 = (k + 1)3 + 3(k + 1)2 + 5(k + 1) chia hết cho 3.
Thật vậy, ta có:
uk+1 = (k + 1)3 + 3(k + 1)2 + 5(k + 1)
= k3 + 3k2 + 3k + 1 + 3(k + 1)2 + 5k + 5
= (k3 + 3k2 + 5k) + 3(k + 1)2 + 3k + 6.
Vì: (k3 + 3k2 + 5k) ⋮ 3, 3(k + 1)2 ⋮ 3, 3k ⋮ 3 và 6 ⋮ 3 nên: uk+1 ⋮ 3.
Vậy mệnh đề đúng với n = k + 1.
Do đó, ta có điều phải chứng minh.
b) Với n = 1 ta có u1 = 91 − 1 = 8 chia hết cho 8.
Vậy mệnh đề đúng với n = 1.
Giả sử mệnh đề đúng với n = k ≥ 1, k ∈ ℕ, tức là uk = 9k − 1 chia hết cho 8.
Ta cần chứng minh: uk+1 = 9k+1 − 1 chia hết cho 8.
Thật vậy, ta có:
uk+1 = 9k+1 − 1 = 9.9k − 9 + 8 = [9.(9k – 1) + 8] ⋮ 8.
Vậy mệnh đề đúng với n = k + 1.
Do đó, ta có điều phải chứng minh.
Câu 3. Chứng minh rằng với mọi số tự nhiên n ≥ 3, ta luôn có:
a) 3n > n2 + 4n + 5.
b) 2n > 2n + 1.
Lời giải
a) Với n = 3 ta thấy bất đẳng thức đã cho đúng.
Giả sử bất đẳng thức đã cho đúng với n = k ≥ 3, k ∈ ℕ, tức là ta có: 3k > k2 + 4k + 5 (1).
Ta cần chứng minh bất đẳng thức đúng với n = k + 1, tức là:
3k+1 > (k + 1)2 + 4(k + 1) + 5 hay 3k+1 > k2 + 6k + 10.
Thật vậy, nhân cả hai vế của bất đẳng thức (1) với 3 ta được:
3.3k > 3(k2 + 4k + 5)
⇔ 3k+1 > k2 + 6k + 10 + 2k2 + 6k + 5
⇒ 3k+1 > k2 + 6k + 10 (vì k ≥ 3).
Vậy bất đẳng thức đã cho đúng với n = k + 1.
Do đó, ta có điều phải chứng minh.
b) Với n = 3 ta thấy bất đẳng thức đã cho đúng.
Giả sử bất đẳng thức đã cho đúng với n = k ≥ 3, k ∈ ℕ, tức là ta có: 2k > 2k + 1 (1)
Ta cần chứng minh bất đẳng thức đúng với n = k + 1, tức là:
2k + 1 > 2(k + 1) + 1 hay 2k + 1 > 2k + 3.
Thật vậy, nhân cả hai vế của bất đẳng thức (1) với 2 ta được:
2.2k > 2(2k + 1) ⇔ 2k+1 > 2k + 2k + 2 (2)
Vì k ≥ 3 nên 2k ≥ 6. Do đó (2) tương đương với:
2k+1 > 2k + 6 + 2 ⇒ 2k+1 > 2k + 3
Vậy bất đẳng thức đã cho đúng với n = k + 1.
Do đó, ta có điều phải chứng minh.
Câu 4. Chứng minh rằng với mọi số nguyên dương n, ta luôn có:
a)
b)
c)
d)
e)
với mọi n ≥ 2, n ∈ ℕ.
f)
Lời giải.
a) Đặt
Với n = 1 thì .
Vậy (1) đúng với n = 1.
Giả sử (1) đúng với n = k ≥ 1, k ∈ ℕ, tức là ta có:
Ta cần chứng minh (1) cũng đúng với n = k + 1, tức là cần chứng minh:
Thật vậy, ta có:
Vậy (1) đúng với n = k + 1. Do đó:
với mọi số tự nhiên n ≥ 1.
b) Đặt
Với n = 1 thì .
Vậy (1) đúng với n = 1.
Giả sử (1) đúng với n = k ≥ 1, k ∈ ℕ, tức là ta có:
Ta cần chứng minh (1) cũng đúng với n = k + 1, tức là cần chứng minh:
Thật vậy, ta có:
Vậy (1) đúng với n = k + 1.
Do đó, với mọi số tự nhiên n ≥ 1.
c) Đặt
Với n = 1 thì
Vậy (1) đúng với n = 1.
Giả sử (1) đúng với n = k ≥ 1, k ∈ ℕ, tức là ta có:
Ta cần chứng minh (1) cũng đúng với n = k + 1, tức là cần chứng minh:
Thật vậy, ta có:
Vậy (1) đúng với n = k + 1.
Do đó, với mọi số tự nhiên n ≥ 1.
d) Đặt
Với n = 1 thì
Vậy (1) đúng với n = 1.
Giả sử (1) đúng với n = k ≥ 1, k ∈ ℕ, tức là ta có:
Ta cần chứng minh (1) cũng đúng với n = k + 1, tức là cần chứng minh:
Thật vậy, ta có:
Vậy (1) đúng với n = k + 1.
Do đó,
với mọi số tự nhiên n ≥ 1.
e) Đặt
Với n = 2 thì
Vậy (1) đúng với n = 2.
Giả sử (1) đúng với n = k ≥ 2, k ∈ ℕ, tức là ta có:
Ta cần chứng minh (1) cũng đúng với n = k + 1, tức là cần chứng minh:
Thật vậy, ta có:
Vậy (1) đúng với n = k + 1.
Do đó,
với mọi số tự nhiên n ≥ 2.
f) Đặt
Với n = 1 thì
Vậy (1) đúng với n = 1.
Giả sử (1) đúng với n = k ≥ 1, k ∈ ℕ, tức là ta có:
Ta cần chứng minh (1) cũng đúng với n = k + 1, tức là cần chứng minh:
Thật vậy, ta có:
Vậy (1) đúng với n = k + 1.
Do đó, với mọi số tự nhiên n ≥ 1.
Câu 5. Chứng minh rằng với mọi số nguyên dương n, ta luôn có:
a) un = n3 + 11n chia hết cho 6.
b) un = 2n3 − 3n2 + n chia hết cho 6.
c) un = 4n + 15n − 1 chia hết cho 9.
d) un = 7.22n−2 + 32n−1 chia hết cho 5.
Lời giải.
a) Với n = 1, ta có: u1 = 13 + 11.1 = 12 chia hết cho 6.
Vậy mệnh đề đúng với n = 1.
Giả sử mệnh đề đúng với n = k ≥ 1, k ∈ ℕ, tức là: uk = k3 + 11k chia hết cho 6.
Ta cần chứng minh uk+1 = (k + 1)3 + 11(k + 1) chia hết cho 6.
Thật vậy, ta có:
uk+1 = (k + 1)3 + 11(k + 1)
= k3 + 3k(k + 1) + 1 + 11k + 11
= k3 + 11k + 3k(k + 1) + 12.
Vì (k3 + 11k) ⋮ 6, 3k(k + 1) ⋮ 6 và 12 ⋮ 6 nên uk+1 ⋮ 6.
Vậy mệnh đề đúng với n = k + 1.
Do đó, ta có điều phải chứng minh.
b) Với n = 1, ta có: u1 = 2.13 – 3.12 + 1 = 0 chia hết cho 6.
Vậy mệnh đề đúng với n = 1.
Giả sử mệnh đề đúng với n = k ≥ 1, k ∈ ℕ, tức là: uk = 2k3 − 3k2 + k chia hết cho 6.
Ta cần chứng minh:
uk+1 = (k + 1)3 − 3(k + 1)2 + (k + 1) chia hết cho 6.
Thật vậy, ta có:
uk+1 = 2(k + 1)3 − 3(k + 1)2 + (k + 1)
= 2k3 + 6k(k + 1) + 2 − 3k2 − 6k − 3 + k + 1
= [(2k3 − 3k2 + k) + 6k(k + 1) − 6k] ⋮ 6.
Vậy mệnh đề đúng với n = k + 1.
Do đó, ta có điều phải chứng minh.
c) Với n = 1, ta có: u1 = 41 + 15.1 − 1 = 18 chia hết cho 9.
Vậy mệnh đề đúng với n = 1.
Giả sử mệnh đề đúng với n = k ≥ 1, k ∈ ℕ, tức là: uk = 4k + 15k − 1 chia hết cho 9.
Ta cần chứng minh: uk+1 = 4k+1 + 15(k + 1) − 1 chia hết cho 9.
Thật vậy, ta có:
uk+1 = 4k+1 + 15(k + 1) − 1
= 4.4k + 60k − 4 − 45k + 18
= [4(4k + 15k – 1) − 45k + 18] ⋮ 9.
Vậy mệnh đề đúng với n = k + 1.
Do đó, ta có điều phải chứng minh.
d) Với n = 1, ta có: u1 = 7.22·1 − 2 + 32·1 − 1 = 10 chia hết cho 5.
Vậy mệnh đề đúng với n = 1.
Giả sử mệnh đề đúng với n = k ≥ 1, k ∈ ℕ, tức là: uk = 7.22k−2 + 32k−1 chia hết cho 5.
Ta cần chứng minh: uk+1 = 7.22(k+1)−2 + 32(k+1)−1 chia hết cho 5.
Thật vậy, ta có:
uk+1 = 7.22(k+1)−2 + 32(k+1)−1
= 4 .7.22k−2 + 9.32k−1
= [4(72k−2 + 32k−1) + 5. 32k−1] ⋮ 5.
Vậy mệnh đề đúng với n = k + 1.
Do đó, ta có điều phải chứng minh.
Câu 6. Chứng minh rằng
a) 2n+2 > 2n + 5 với mọi n ∈ ℕ.
b) nn ≥ (n + 1)n−1 với mọi n ∈ ℕ*.
Lời giải.
a) Với n = 1 ta thấy bất đẳng thức đã cho đúng.
Giả sử bất đẳng thức đã cho đúng với n = k ≥ 1, k ∈ ℕ, tức là ta có: 2k+2 > 2k + 5 (1)
Ta cần chứng minh bất đẳng thức đúng với n = k + 1, tức là:
2(k+1)+2 > 2(k + 1) + 5 hay 2k+3 > 2k + 7.
Thật vậy, nhân cả hai vế của bất đẳng thức (1) với 2 ta được
2.2k+2 > 2(2k + 5)
⇔ 2k+3 > 2k + 7 + 2k + 3
⇒ 2k+3 > 2k + 7 (vì k ≥ 1 nên 2k + 3 > 0).
Vậy bất đẳng thức đã cho đúng với n = k + 1.
Do đó, ta có điều phải chứng minh.
b) Với n = 1 ta thấy bất đẳng thức đã cho đúng.
Giả sử bất đẳng thức đã cho đúng với n = k ≥ 1, k ∈ ℕ, tức là ta có:
Ta cần chứng minh bất đẳng thức đúng với n = k + 1, tức là:
(k + 1)k+1 ≥ [(k + 1) + 1](k+1)−1 hay (k + 1)k+1 ≥ (k + 2)k.
Thật vậy, với mọi số dương k ta có:
Vậy bất đẳng thức đã cho đúng với n = k + 1.
Do đó, ta có điều phải chứng minh.
Câu 7. Chứng minh rằng với mọi số nguyên dương n, ta luôn có:
a)
b)
c)
d)
e)
f) , với mọi n ≥ 2, n ∈ ℕ.
g)
Lời giải.
a) Đặt
Với n = 1 thì
Vậy (1) đúng với n = 1.
Giả sử (1) đúng với n = k ≥ 1, k ∈ ℕ, tức là ta có:
Ta cần chứng minh (1) cũng đúng với n = k + 1, tức là cần chứng minh:
Thật vậy, ta có:
Vậy (1) đúng với n = k + 1.
Do đó, với mọi số tự nhiên n ≥ 1.
b) Đặt
Với n = 1 thì
Vậy (1) đúng với n = 1.
Giả sử (1) đúng với n = k ≥ 1, k ∈ ℕ, tức là ta có:
Ta cần chứng minh (1) cũng đúng với n = k + 1, tức là cần chứng minh:
Thật vậy, ta có:
Vậy (1) đúng với n = k + 1.
Do đó,
với mọi số tự nhiên n ≥ 1.
c) Đặt:
Với n = 1 thì
Vậy (1) đúng với n = 1.
Giả sử (1) đúng với n = k ≥ 1, k ∈ ℕ, tức là ta có:
Ta cần chứng minh (1) cũng đúng với n = k + 1, tức là cần chứng minh:
Thật vậy, ta có:
Vậy (1) đúng với n = k + 1. Do đó:
với mọi số tự nhiên n ≥ 1.
d) Đặt
Với n = 1 thì
Vậy (1) đúng với n = 1.
Giả sử (1) đúng với n = k ≥ 1, k ∈ ℕ, tức là ta có:
Ta cần chứng minh (1) cũng đúng với n = k + 1, tức là cần chứng minh:
Thật vậy, ta có:
Vậy (1) đúng với n = k + 1. Do đó:
với mọi số tự nhiên n ≥ 1.
e) Đặt
Với n = 1, thì:
Vậy (1) đúng với n = 1.
Giả sử (1) đúng với n = k ≥ 1, k ∈ ℕ, tức là ta có:
Ta cần chứng minh (1) cũng đúng với n = k + 1, tức là cần chứng minh:
Thật vậy, ta có:
Vậy (1) đúng với n = k + 1. Do đó:
với mọi số tự nhiên n ≥ 1.
f) Đặt:
Với n = 2 thì
Vậy (1) đúng với n = 2.
Giả sử (1) đúng với n = k ≥ 2, k ∈ ℕ, tức là ta có:
Ta cần chứng minh (1) cũng đúng với n = k + 1, tức là cần chứng minh:
Thật vậy, ta có:
Vậy (1) đúng với n = k + 1. Do đó:
với mọi số tự nhiên n ≥ 2.
g) Đặt:
Với n = 1, thì
Vậy (1) đúng với n = 1.
Giả sử (1) đúng với n = k ≥ 1, k ∈ ℕ, tức là ta có:
Ta cần chứng minh (1) cũng đúng với n = k + 1, tức là cần chứng minh:
Thật vậy, ta có:
Vậy (1) đúng với n = k + 1.
Do đó, với mọi số tự nhiên n ≥ 1.
Câu 8. Chứng minh rằng với mọi số nguyên dương n, ta luôn có:
a) un = n3 − n chia hết cho 3.
b) un = 13n − 1 chia hết cho 6.
c) un = 4n + 6n + 8 chia hết cho 9.
d) un = 32n+1 + 2n+2 chia hết cho 7.
e) un = 11n+1 + 122n−1 chia hết cho 133.
f) un = 24n − 1 chia hết cho 15.
Lời giải.
a) Với n = 1, ta có: u1 = 13 − 1 = 0 chia hết cho 3.
Vậy mệnh đề đúng với n = 1.
Giả sử mệnh đề đúng với n = k ≥ 1, k ∈ ℕ, tức là: uk = k3 − k chia hết cho 3.
Ta cần chứng minh: uk+1 = (k + 1)3 − (k + 1) chia hết cho 3.
Thật vậy, ta có:
uk+1 = (k + 1)3 − (k + 1)
= k3 + 3k2 + 2k
= k3 − k + 3(k2 + k).
Vì (k3 – k) ⋮ 3, 3(k2 + k) ⋮ 3 nên uk+1 ⋮ 3.
Vậy mệnh đề đúng với n = k + 1.
Do đó, ta có điều phải chứng minh.
b) Với n = 1, ta có: u1 = 133 − 1 = 12 chia hết cho 6.
Vậy mệnh đề đúng với n = 1.
Giả sử mệnh đề đúng với n = k ≥ 1, k ∈ ℕ, tức là: uk = 13k − 1 chia hết cho 6.
Ta cần chứng minh: uk+1 = 13k − 1 chia hết cho 6.
Thật vậy, ta có:
uk+1 = 13k − 1
= 13k+1 – 13 + 12
= 13(13k – 1) + 12
Vì 13(13k – 1) ⋮ 6, 12 ⋮ 6 nên uk+1 ⋮ 6.
Vậy mệnh đề đúng với n = k + 1.
Do đó, ta có điều phải chứng minh.
c) Với n = 1, ta có: u1 = 41 + 6.1 + 8 = 18 chia hết cho 9.
Vậy mệnh đề đúng với n = 1.
Giả sử mệnh đề đúng với n = k ≥ 1, k ∈ ℕ, tức là: uk = 4k + 6k + 8 chia hết cho 9.
Ta cần chứng minh: uk+1 = 4k+1 + 6(k + 1) + 8 chia hết cho 9.
Thật vậy, ta có:
uk+1 = 4k+1 + 6(k + 1) + 8
= 4(4k + 6k + 8) – 18k – 18
= 4(4k + 6k + 8) – 18(k + 1)
Vì 4(4k + 6k + 8) ⋮ 9, 18(k + 1) ⋮ 9 nên uk+1 ⋮ 9.
Vậy mệnh đề đúng với n = k + 1.
Do đó, ta có điều phải chứng minh.
d) Với n = 1, ta có: u1 = 31+1 + 21+2 = 35 chia hết cho 7.
Vậy mệnh đề đúng với n = 1.
Giả sử mệnh đề đúng với n = k ≥ 1, k ∈ ℕ, tức là: uk = 32k+1 + 2k+2 chia hết cho 7.
Ta cần chứng minh: uk+1 = 32(k+1)+1 + 2(k+1)+2 chia hết cho 7.
Thật vậy, ta có:
uk+1 = 32(k+1)+1 + 2(k+1)+2
= 32k+3 + 2k+3
= 9(32k+1 + 2k+2) – 7.2k
Vì 9(32k+1 + 2k+2) ⋮ 7, 7.2k ⋮ 7 nên uk+1 ⋮ 7.
Vậy mệnh đề đúng với n = k + 1.
Do đó, ta có điều phải chứng minh.
e) Với n = 1, ta có: u1 = 111+1 + 121−1 = 133 chia hết cho 133.
Vậy mệnh đề đúng với n = 1.
Giả sử mệnh đề đúng với n = k ≥ 1, k ∈ ℕ, tức là: uk = 11k+1 + 122k−1 chia hết cho 133.
Ta cần chứng minh: uk+1 = 11k+2 + 122(k+1)−1 chia hết cho 133.
Thật vậy, ta có:
uk+1 = 11k+2 + 122(k+1)−1
= 11.11k+1 + 122.122k−1
= [11(11k+1 – 122k−1) – 133.122k−1] ⋮ 133
Vậy mệnh đề đúng với n = k + 1.
Do đó, ta có điều phải chứng minh.
e) Với n = 1, ta có: u1 = 21 – 1 = 15 chia hết cho 15.
Vậy mệnh đề đúng với n = 1.
Giả sử mệnh đề đúng với n = k ≥ 1, k ∈ ℕ, tức là: uk = 24k – 1 chia hết cho 15.
Ta cần chứng minh: uk+1 = 24(k+1) – 1 chia hết cho 15.
Thật vậy, ta có:
uk+1 = 24(k+1) – 1
= 24k+4 – 1
= 16.24k – 1
= 16.24k – 16 + 15
= 16(24k – 1) + 15
Vì 16(24k – 1) ⋮ 15, 15 ⋮ 15 nên uk+1 ⋮ 15.
Vậy mệnh đề đúng với n = k + 1.
Do đó, ta có điều phải chứng minh.
Câu 9. Chứng minh rằng:
a) 2n+1 > 2n + 3 với mọi n ≥ 2, n ∈ ℕ.
b) 3n−1 > n(n + 2) với mọi n ≥ 4, n ∈ ℕ.
c) (n!)2 ≥ nn với mọi n ∈ ℕ*.
d) 2n > n2 với mọi n ≥ 5, n ∈ ℕ.
Lời giải.
a) Với n = 2 ta thấy bất đẳng thức đã cho đúng.
Giả sử bất đẳng thức đã cho đúng với n = k ≥ 2, k ∈ ℕ, tức là ta có: 2k+1 > 2k + 3 (1).
Ta cần chứng minh bất đẳng thức đúng với n = k + 1, tức là:
2(k+1)+1 > 2(k + 1) + 3 hay 2k+2 > 2k + 5.
Thật vậy, nhân cả hai vế của bất đẳng thức (1) với 2 ta được:
2.2k+1 > 2(2k + 3)
⇔ 2k+2 > 2k + 5 + 2k + 1 (2)
Vì k ≥ 2 nên 2k + 1 > 0. Khi đó từ (2) suy ra:
2k+2 > 2k + 5.
Vậy bất đẳng thức đã cho đúng với n = k + 1.
Do đó, ta có điều phải chứng minh.
b) Với n = 4 ta thấy bất đẳng thức đã cho đúng.
Giả sử bất đẳng thức đã cho đúng với n = k ≥ 4, k ∈ ℕ, tức là ta có: 3k−1 > k(k + 2) (1)
Ta cần chứng minh bất đẳng thức đúng với n = k + 1, tức là:
3(k+1)−1 > (k + 1)[(k + 1) + 2] hay 3k > (k + 1)(k + 3).
Thật vậy, nhân cả hai vế của bất đẳng thức (1) với 3 ta được:
3.3k−1 > 3k(k + 2)
⇔ 3k > k2 + 4k + 3 + 2k2 + 2k − 3 (2)
Vì k ≥ 4 và 2k2 + 2k − 3 = 2k(k − 4) + 10(k − 4) + 37.
Nên 2k2 + 2k − 3 > 0.
Khi đó từ (2) suy ra:
3k > k2 + 4k + 3 ⇔ 3k > (k + 1)(k + 2).
Vậy bất đẳng thức đã cho đúng với n = k + 1.
Do đó, ta có điều phải chứng minh.
c) Trước hết ta chứng minh nn ≥ (n + 1)n−1.
Thật vậy, với n = 1 ta được khẳng định đúng.
Giả sử khẳng định đúng với n = k ≥ 1, tức là ta có:
hay
Ta cần chứng minh khẳng định cũng đúng khi n = k + 1. Ta có:
Vậy nn ≥ (n + 1)n−1 với mọi n ∈ ℕ*.
Trở lại bài toán. Ta cũng chứng minh bài toán bằng quy nạp.
Với n = 1 ta thấy bất đẳng thức đã cho đúng.
Giả sử bất đẳng thức đã cho đúng với n = k ≥ 1, k ∈ ℕ, tức là ta có: (k!)2 ≥ kk (1).
Ta cần chứng minh bất đẳng thức đúng với n = k + 1, tức là: [(k + 1)!]2 ≥ (k + 1)k+1.
Thật vậy, ta có:
[(k + 1)!]2 = [k!(k + 1)]2 = (k!)2(k + 1)2
≥ kk(k + 1)2 ≥ (k + 1)k−1(k + 1)2 = (k + 1)k+1.
Vậy bất đẳng thức đã cho đúng với n = k + 1.
Do đó, ta có điều phải chứng minh.
d) Trước hết, bằng phương pháp quy nạp ta chứng minh trước kết quả n2 > 2n + 1 với mọi n ∈ ℕ, n ≥ 5.
Với n = 5 ta thấy bất đẳng thức là đúng.
Giả sử bất đẳng thức trên đúng với n = k ≥ 5, k ∈ ℕ, tức là ta có: k2 > 2k + 1.
Ta cần chứng minh bất đẳng thức đúng với n = k + 1, tức là (k + 1)2 > 2(k + 1) + 1.
Thật vậy, ta có:
(k + 1)2 = k2 + 2k + 1
> 2k + 1 + 2k + 1 = 4k + 2
> 3k + 3 > 2k + 3.
Vậy n2 > 2n + 1 với mọi n ≥ 5, n ∈ ℕ.
Trở lại với bài toán.
Với n = 5 ta thấy bất đẳng thức đã cho đúng.
Giả sử bất đẳng thức đã cho đúng với n = k ≥ 5, k ∈ ℕ, tức là ta có 2k > k2 (1)
Ta cần chứng minh bất đẳng thức đúng với n = k + 1, tức là 2k+1 > (k + 1)2.
Thật vậy, nhân cả hai vế của bất đẳng thức (1) với 2 ta được:
2.2k > 2k2
⇔ 2k+1 > k2 + k2
⇔ 2k+1 > k2 + 2k + 1
⇔ 2k+1 > (k + 1)2.
Vậy bất đẳng thức đã cho đúng với n = k + 1.
Do đó, ta có điều phải chứng minh.
Bạn đang xem bài viết Phân dạng bài tập có lời giải xem thêm các bài viết khác về chủ đề Toán lớp 11. Chúc bạn 1 ngày vui vẻ!