Bạn đang xem bài viết Tổng quan lý thuyết & bài tập. Hi vọng sẽ là đáp án bạn ưng ý. Cùng theo dõi nhé!
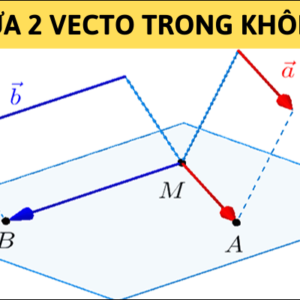
Ở bài viết này, Cấp Nước Lào Cai sẽ giúp bạn tổng hợp lý thuyết và một số dạng toán liên quan đến chủ đề hai đường thẳng song song trong không gian.
Lý thuyết hai đường thẳng song song
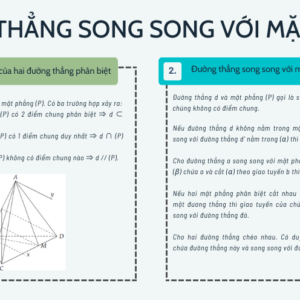
1. Vị trí tương đối của hai đường thẳng phân biệt
Cho hai đường thẳng phân biệt a, b.
 Hình ảnh minh họa 2 đường thẳng cắt nhau
Hình ảnh minh họa 2 đường thẳng cắt nhau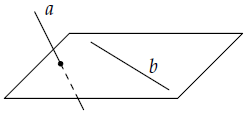 Hình ảnh minh họa 2 đường thẳng chéo nhau
Hình ảnh minh họa 2 đường thẳng chéo nhau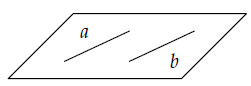 Hình ảnh minh họa 2 đường thẳng song song
Hình ảnh minh họa 2 đường thẳng song song
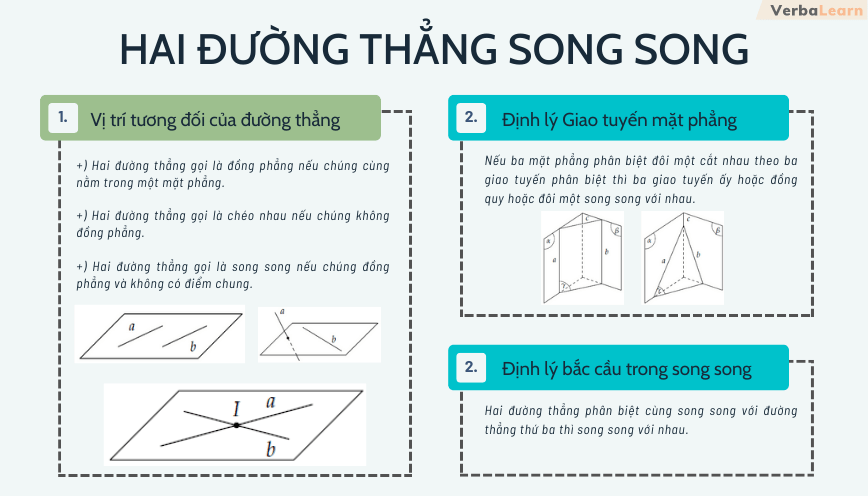
+) Hai đường thẳng gọi là đồng phẳng nếu chúng cùng nằm trong một mặt phẳng.
+) Hai đường thẳng gọi là chéo nhau nếu chúng không đồng phẳng.
+) Hai đường thẳng gọi là song song nếu chúng đồng phẳng và không có điểm chung.
2. Tính chất hai đường thẳng song song
Định lí 1
Trong không gian, qua một điểm không nằm trên đường thẳng cho trước, có một và chỉ một đường thẳng song song với đường thẳng đã cho.
Định lí 2 – Định lí về giao tuyến của ba mặt phẳng
Nếu ba mặt phẳng phân biệt đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc đôi một song song với nhau.
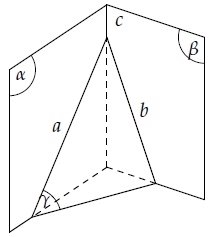
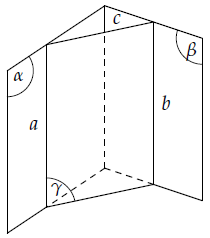
Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) cũng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
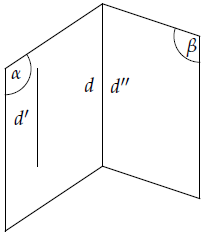
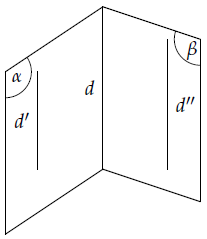
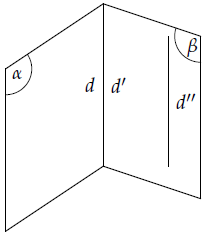
Định lí 3
Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau.
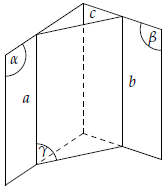
Dạng 1. Chứng minh hai đường thẳng song song.
Phương pháp giải
Cách 1. Chứng minh hai đường thẳng a, b đồng phẳng, rồi dùng các định lí trong hình học phẳng, chẳng hạn định lí đường trung bình, định lí đảo Thales,… để chứng minh a // b.
Cách 2. Chứng minh hai đường thẳng đó cùng song song với đường thẳng thứ ba. Chẳng hạn, chứng minh.
Cách 3. Áp dụng định lí về giao tuyến của ba mặt phẳng và hệ quả của nó. Chẳng hạn, chứng minh
Bài tập vận dụng
Câu 1. Cho tứ diện ABCD có I, J lần lượt là trọng tâm của tam giác ABC và ABD. Chứng minh rằng IJ // CD.
Lời giải
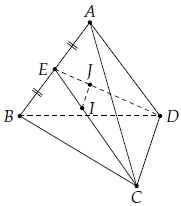
Gọi E là trung điểm AB.
Ta có ⇒ IJ và CD đồng phẳng.
Vì I, J lần lượt là trọng tâm của tam giác ABC và ABD nên
Theo định lí đảo Thales suy ra IJ // CD (đpcm).
Câu 2 Cho tứ diện ABCD. Gọi M, N, P, Q, R, S lần lượt là trung điểm của AB, CD, BC, AD, AC, BD. Chứng minh MPNQ là hình bình hành. Từ đó suy ra ba đoạn thẳng MN, PQ, RS cắt nhau tại trung điểm G của mỗi đoạn.
Lời giải
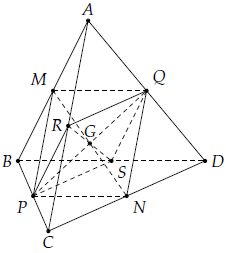
Vì MP là đường trung bình của ΔABC nên
(1)
Vì NQ là đường trung bình của ∆ACD nên
(2)
Từ (1) và (2) suy ra
Do đó, MPNQ là hình bình hành. Suy ra MN, PQ cắt nhau tại trung điểm G của mỗi đoạn.
Chứng minh tương tự ta được PSQR là hình bình hành nên PQ, RS cắt nhau tại trung điểm G của mỗi đoạn.
Vậy MN, PQ, RS cắt nhau tại trung điểm G của mỗi đoạn.
Nhận xét. Điểm G nói trên được gọi là trọng tâm của tứ diện.
Trọng tâm của tứ diện là điểm đồng quy của các đoạn nối trung điểm của các cạnh đối, nó cũng là trung điểm của các cạnh này.
Câu 3. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm của SA, SD. Chứng minh
1) MN // AD và MN // BC;
2) MO // SC và NO // SB.
Lời giải
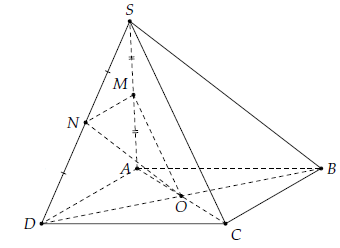
1) Xét tam giác SAD có
+) M là trung điểm của SA (giả thiết);
+) N là trung điểm của SD (giả thiết).
Suy ra MN là đường trung bình của ΔSAD. Do đó MN // AD.
Ta có MN // AD (chứng minh trên)
BC // AD (ABCD là hình bình hành)
⇒ MN // BC
2) Xét tam giác ASC có
+) M là trung điểm của SA (giả thiết);
+) O là trung điểm của AC (O là tâm của hình bình hành ABCD).
Suy ra OM là đường trung bình của ∆SAC. Do đó MO // SC.
Tương tự, NO là đường trung bình của ∆SDB nên NO // SB.
Câu 4. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm của AB, AD. Gọi I, J, G lần lượt là trọng tâm của các tam giác SAB, SAD và AOD. Chứng minh
1) IJ // MN
2) IJ // BD và GJ // SO.
Lời giải.
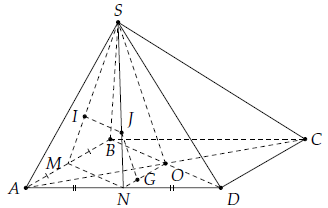
1) Xét tam giác SMN có
+) (I là trọng tâm của ΔSAB);
+) (J là trọng tâm của ΔSAD).
Suy ra IJ // MN (định lý Ta–lét đảo).
2) Vì MN là đường trung bình của ΔABD nên MN // BD.
Mà IJ // MN (chứng minh trên) nên IJ // BD.
Xét tam giác SON có
+) (G là trọng tâm của ΔAOD);
+) (J là trọng tâm của ΔSAD).
Suy ra GJ // SO (định lý Ta–lét đảo).
Câu 5. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O và I là một điểm trên cạnh SO.
1) Tìm giao điểm E và F của mặt phẳng (ICD) lần lượt với các đường SA, SB. Chứng minh EF // AB;
2) Gọi K là giao điểm của DE và CF. Chứng minh SK // BC.
Lời giải.
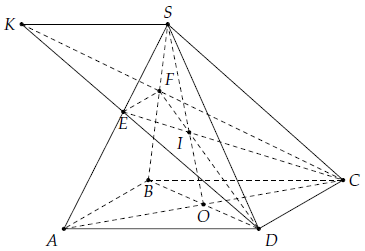
1) Vì I ∈ SO mà SO ⊂ (SBD) nên I ∈ (SBD). Do đó F = D I ∩ SB và E = C I ∩ SA.
Ta có
+) (CDI) ∩ (ABCD) = CD
+) (SAB) ∩ (ABCD) = AB
+) (CDI) ∩ (SAB) = EF
Mà AB // CD (ABCD là hình bình hành) nên EF // AB // CD (tính chất giao tuyến của ba mặt phẳng).
2) Cách 1. Ta có
+) ⇒ K là điểm chung thứ nhất của hai mặt phẳng (SAD) và (SBC).
+) ⇒ S là điểm chung thứ hai của hai mặt phẳng (SAD) và (SBC).
Suy ra SK là giao tuyến của hai mặt phẳng (SAD) và (SBC).
Ta có ⇒ SK // BC // AD
Vậy SK // BC.
Cách 2. Trong ∆SCD có EF // CD nên theo định lý Ta–lét ta có
(1)
Tương tự, trong ΔSAB có EF // AB nên
(2)
Từ (1) và (2) suy ra:
Xét ΔFSK và ΔFBC có
+) (chứng minh trên)
+) (đối đỉnh)
Do đó ∆FSK ∽ ∆FBC (cạnh – góc – cạnh) suy ra SK // BC.
Câu 6. Cho hình chóp SABCD có đáy ABCD là hình thang đáy lớn AB. Gọi E, F lần lượt là trung điểm của SA và SB.
1) Chứng minh EF // CD
2) Tìm I = AF ∩ (SCD)
3) Chứng minh SI // AB // CD
Lời giải.
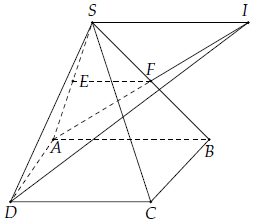
1) Ta có EF là đường trung bình của tam giác SAB nên EF // AB
Mà AB // CD (hai đáy của hình thang)
Nên EF // CD.
2) Hai mặt phẳng (SAB) và (SCD) có AB // CD nên giao tuyến là đường thẳng Sx // AB // CD.
Kéo dài AF cắt Sx tại I.
Ta thấy I là điểm chung của AF và (SCD).
3) Theo ý 2)
Dạng 2. Tìm giao tuyến của hai mặt phẳng chứa hai đường thẳng song song.
Phương pháp giải
⇒ (α) ∩ (β) = Ax với Ax // a // b
Bài tập vận dụng
Câu 1. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Điểm M thuộc cạnh SA. Điểm E, F lần lượt là trung điểm của AB và BC.
1) Tìm (SAB) ∩ (SCD)
2) Tìm (MBC) ∩ (SAD)
3) Tìm (MEF) ∩ (SAC)
4) Tìm AD ∩ (MEF)
5) Tìm SD ∩ (MEF)
6) Tìm thiết diện của hình chóp cắt bởi (MEF)
Lời giải
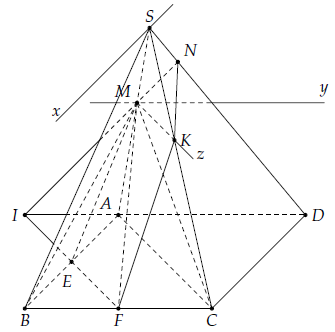
1)
⇒ (SAB) ∩ (SCD) = Sx với Sx // AB // CD
2)
⇒ (MBC) ∩ (SAD) = My với My // BC // AD
3)
⇒ (MEF) ∩ (SAC) = Mz với Mz // EF // AC
4) Trong (ABCD), gọi I = EF ∩ AD
Mà EF ⊂ (MEF) nên AD ∩ (MEF) = I
5) Trong (SAD), gọi N = SD ∩ IM
Mà IM ⊂ (MEF) nên SD ∩ (MEF) = N
6) Thiết diện của hình chóp cắt bởi (MEF) là ngũ giác MNKFE.
Câu 2. Cho hình chóp S.ABCD. Mặt đáy là hình thang có cạnh đáy lớn AD, AB cắt CD tại điểm K. Gọi M là điểm nằm trên cạnh SD.
1) Tìm d = (SAD) ∩ (SBC) và N = KM ∩ (SBC)
2) Chứng minh rằng AM, BN và d đồng quy.
Lời giải
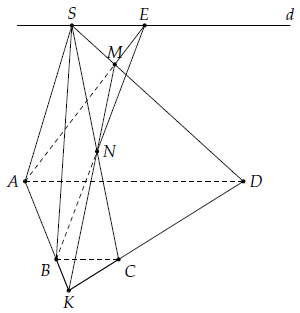
1)
⇒ (SAD) ∩ (SBC) = d với S ∈ d, d // AD // BC
Trong (SCD), gọi N = KM ∩ SC.
Mà SC ⊂ (SBC) nên N = KM ∩ (SBC)
2)
Theo định lí về giao tuyến của 3 mặt phẳng, suy ra AM, BN và d hoặc đồng quy hoặc đôi một song song.
Mà AM, d cắt nhau nên AM, BN và d phải đồng quy.
Câu 3. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của SA, SB. Gọi P là một điểm trên cạnh BC. Tìm giao tuyến của
1) (SBC) và (SAD)
2) (SAB) và (SCD)
3) (MNP) và (ABCD).
Lời giải.
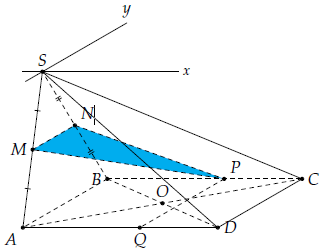
1) Ta có
+) (SBC) ∩ (ABCD) = BC
+) (SAD) ∩ (ABCD) = AD
+) AD // BC (ABCD là hình bình hành).
Mà S là điểm chung của 2 mặt phẳng (SBC) và (SAD) nên giao tuyến của 2 mặt phẳng (SBC) và (SAD) là đường thẳng Sx // BC // AD.
2) Giao tuyến của hai mặt phẳng (SAB) và (SCD) là đường thẳng Sy // AB // CD.
3) Vì MN // AB (MN là đường trung bình của ∆SAB) nên qua P kẻ PQ // AB (Q ∈ AD).
Khi đó giao tuyến của hai mặt phẳng (MNP) và (ABCD) là đường thẳng PQ.
Câu 4. Cho tứ diện SABC. Gọi E và F lần lượt là trung điểm của các cạnh SB và AB, G là một điểm trên cạnh AC. Tìm giao tuyến của các cặp mặt phẳng sau
1) (SAC) và (EFC)
2) (SAC) và (EFG).
Lời giải.
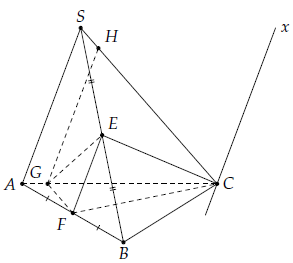
1) Ta có
+) (SAC) ∩ (SAB) = SA
+) (EFC) ∩ (SAB) = EF
+) SA // EF (EF là đường trung bình của ∆SAB).
Do đó giao tuyến của 2 mặt phẳng (SAC) và (EFC) sẽ song song với SA và EF.
Mà C là điểm chung của 2 mặt phẳng (SAC) và (EFC) nên giao tuyến của chúng là đường thẳng Cx // SA // EF.
2) Vì EF // SA (EF là đường trung bình của ∆SAB) nên qua G kẻ GH // SA (H ∈ SC).
Khi đó giao tuyến của hai mặt phẳng (SAC) và (EFG) là đường thẳng GH.
Câu 5. Cho hình chóp S.ABCD có O là tâm của hình bình hành ABCD, điểm M thuộc cạnh SA sao cho SM = 2MA, N là trung điểm của AD.
1) Tìm giao tuyến của mặt phẳng (SAD) và (MBC).
2) Tìm giao điểm I của SB và (CMN), giao điểm J của SA và (ICD).
3) Chứng minh ba đường thẳng ID, JC, SO đồng quy tại E. Tính tỉ số .
Lời giải.
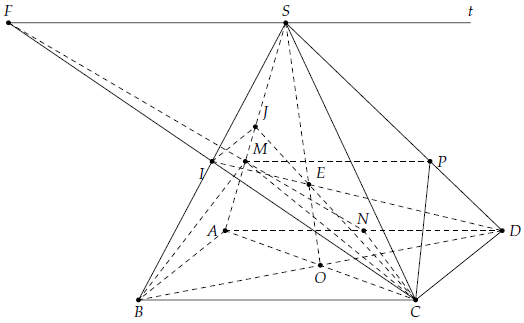
1) Vì
Nên (SAD) ∩ (MBC) = MP // BC // AD (với P ∈ SD)
2) Vì
Nên (SAD) ∩ (SBC) = St // AD // BC.
Gọi F = MN ∩ St; I = CF ∩ SB.
Vì nên I = SB ∩ (CMN).
Qua I kẻ đường thẳng song song với AB cắt SA tại J.
Vì
Nên J = SA ∩ (ICD).
3) Xét 3 mặt phẳng (SAC), (SBD) và (CDJI), ta có
Do đó ba đường thẳng ID, JC, SO đồng quy. Gọi điểm đồng quy là E.
Trong mặt phẳng (SFAD), áp dụng định lý Thales (để ý rằng AN // SF) ta có
Suy ra SF = AD = BC và SFBC là hình bình hành.
I = SB ∩ CF nên I là trung điểm của SB.
∆SBD có DI và SO là trung tuyến nên E là trọng tâm của ∆SBD.
Vậy
Câu 6. Cho hình chóp S.ABCD có đáy ABCD là hình thang với AD là đáy lớn và AD = 2BC. Gọi M, N, P lần lượt thuộc các đoạn SA, AD, BC sao cho MA = 2MS, NA = 2ND, PC = 2PB.
1) Tìm giao tuyến của các cặp mặt phẳng sau: (SAD) và (SBC), (SAC) và (SBD).
2) Xác định giao điểm Q của SB với (MNP).
3) Gọi K là trung điểm của SD. Chứng minh CK = (MQK) ∩ (SCD).
Lời giải
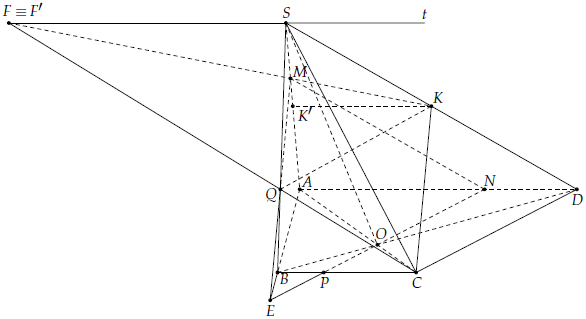
1) Vì
Nên (SAD) ∩ (SBC) = St // AD // BC.
Gọi O = AC ∩ BD ⇒
Suy ra: SO = (SAC) ∩ (SBD).
2) Gọi E = NP ∩ AB và Q = EM ∩ SB.
Vì nên Q = SB ∩ (MNP).
3) Gọi F = MK ∩ St và F’ = QC ∩ St.
Dựa vào các vị trí các điểm Q, C, M và K của giả thiết cho, dễ thấy F và F’ cùng nằm về một phía so với mặt phẳng (SAB).
Trong mặt phẳng (SF’BC), áp dụng định lý Thales (để ý rằng SF’ // BC) ta có:
Gọi K’ là trung điểm của SA. Suy ra
Trong mặt phẳng (SFAD), áp dụng định lý Thales (để ý rằng SF // KK’ ) ta có:
Từ (1), (2) và AD = 2BC suy ra SF = SF’ . Do đó F ≡ F’, suy ra bốn điểm Q, C, M và K đồng phẳng.
Vậy CK = (MQK) ∩ (SCD).
Câu 7. Cho tứ diện ABCD. Gọi G, J lần lượt là trọng tâm tam giác BCD và ACD.
1) Chứng minh GJ // AB
2) Tìm (ABD) ∩ (GJD)
Lời giải.
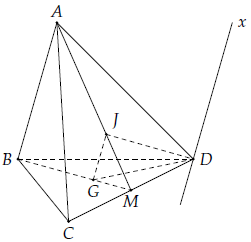
1) Gọi M là trung điểm CD.
Xét tam giác ABM có
Suy ra GJ // AB.
2) Hai mặt phẳng (ABD) và (GJD) có điểm D chung và GJ // AB nên giao tuyến là đường thẳng Dx // G J // AB.
Câu 8. Cho tứ diện ABCD. Gọi I, J lần lượt là trọng tâm ∆ABC, ∆ABD và E, F lần lượt là trung điểm BC, AC.
1) Chứng minh IJ // CD.
2) Tìm (DEF) ∩ (ABD)
Lời giải.
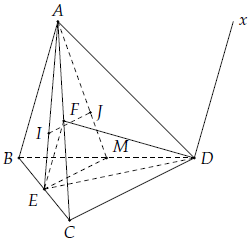
1) Gọi M là trung điểm BD.
Tam giác AEM có nên IJ // ME.
Mà ME // CD (đường trung bình)
Suy ra IJ // CD.
2) Hai mặt phẳng (DEF) và (ABD) có điểm chung D và EF // AB nên giao tuyến là đường thẳng Dx // AB // EF.
Câu 9. Cho hình chóp SABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm của SC và N là trọng tâm tam giác ABC.
1) Tìm I = SD ∩ (AMN)
2) Chứng minh NI // SB
3) Tìm (AMN) ∩ (SAD).
Lời giải.
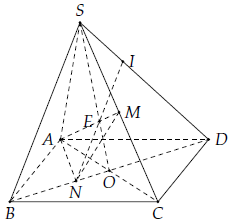
1) Gọi O là giao điểm AC và BD, E là giao điểm SO và AM.
Khi đó NE và SD cắt nhau tại I.
Ta thấy I ∈ SD và I ∈ NE ⊂ (AMN) nên I = SD ∩ (AMN).
2) Tam giác SOB có nên NE // SB.
Suy ra NI // SB.
3) Hai mặt phẳng (AMN) và (SAD) có hai điểm chung A, I nên (AMN) ∩ (SAD) = AI.
Câu 10. Cho hình chóp SABCD có đáy ABCD là hình thang (AB // CD) với CD = 2AB. Gọi O là giao điểm của AC và BD, K là trung điểm SC, G là trọng tâm tam giác SCD.
1) Chứng minh OG // BK
2) Tìm (ACG) ∩ (SBC).
Lời giải.
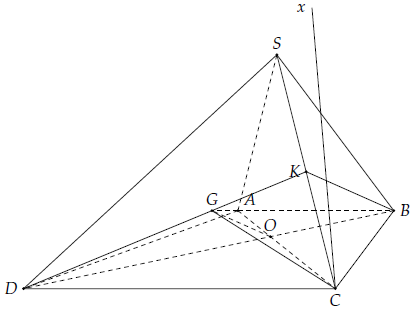
1) Ta có ∆OCD ∽ ∆OAB do và
.
Suy ra:
Suy ra:
Tam giác DBK có nên OG // BK.
2) Hai mặt phẳng (SBC) và (ACG) có điểm C chung và OG // BK nên giao tuyến là đường thẳng Cx // OG // BK.
Câu 11. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và O là giao điểm hai đường chéo AC và BD. Lấy điểm E trên cạnh SC sao cho EC = 2ES.
1) Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD)
2) Tìm giao điểm M của đường thẳng AE và mặt phẳng (SBD). Chứng minh M là trung điểm của đoạn thẳng SO.
Lời giải.
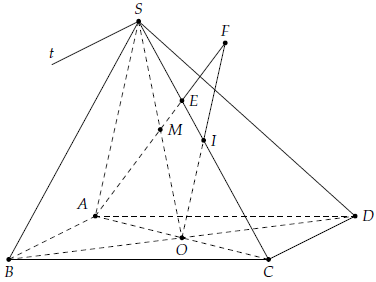
1) Vì
Nên (SAB) ∩ (SCD) = St // AB // CD.
2) Gọi M = AE ∩ SO.
Vì nên M = AE ∩ (SBD).
Gọi I là trung điểm SC, suy ra .
Gọi F = OI ∩ AE. Trong mặt phẳng (SAC), áp dụng định lý Thales (để ý rằng OI // SA)
Suy ra , từ đó dẫn đến SFOA là hình bình hành.
Vậy M là trung điểm của SO.
Câu 12. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, gọi M, N, P lần lượt là trung điểm của SD, CD, BC.
1) Tìm giao tuyến của các cặp mặt phẳng sau: (SAC) và (SBC), (AMN) và (SBC).
2) Tìm giao điểm I của (PMN) và AC, K của (PMN) và SA.
3) Gọi F là trung điểm của PM, chứng minh ba điểm K, F, I thẳng hàng.
Lời giải.
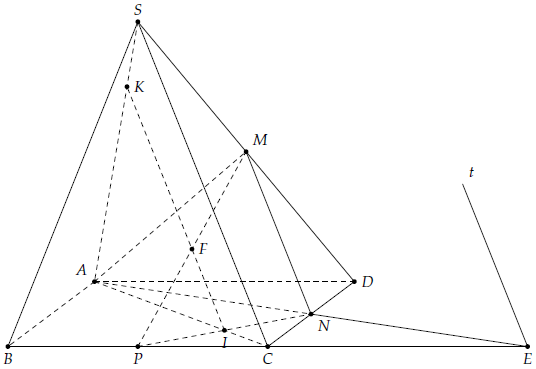
1) Dễ thấy SC = (SAC) ∩ (SBC).
Gọi E = BC ∩ AN
Ta có
Suy ra (SBC) ∩ (AMN) = Et // SC // MN.
2) Gọi I = AC ∩ PN ⇒ ⇒ I = AC ∩ (PMN).
Gọi K là giao điểm của SA với đường thẳng đi qua I và song song với SC.
Vì nên K = SA ∩ (PMN).
3) Theo cách dựng ta có IK // MN. (1)
ABCD là hình bình hành nên AC và BD cắt nhau tại trung điểm mỗi đường.
Mà PN là đường trung bình của ∆CBD nên AC cũng cắt PN tại I là trung điểm của PN.
Suy ra IF là đường trung bình của ∆PMN ⇒ IF // MN. (2)
(1) và (2) suy ra K, F, I thẳng hàng.
Bạn đang xem bài viết Tổng quan lý thuyết & bài tập xem thêm các bài viết khác về chủ đề Toán lớp 11. Chúc bạn 1 ngày vui vẻ!