Bạn đang xem bài viết Lý thuyết và 4 dạng bài tập. Hi vọng sẽ là đáp án bạn ưng ý. Cùng theo dõi nhé!
Bài viết dưới đây Cấp Nước Lào Cai sẽ trình bày đến bạn đọc tổng quan lý thuyết về hai mặt phẳng vuông góc trong không gian. Điểm kiến thức này là nền tảng cho 4 dạng toán hình học không gian thường gặp trong chương trình toán lớp 11.

Lý thuyết góc giữa hai mặt phẳng
Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.
Hai mặt phẳng song song hoặc trùng nhau thì góc giữa chúng bằng 0°.
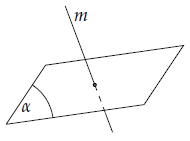
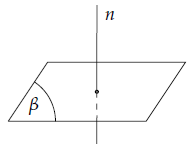
1. Cách xác định góc của hai mặt phẳng cắt nhau
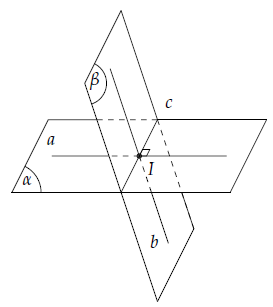
+) Tìm giao tuyến c của (α) và (β).
+) Tìm hai đường thẳng a, b lần lượt thuộc hai mặt phẳng và cùng vuông góc với c tại một điểm.
+) Góc giữa (α) và (β) là góc giữa a và b.
2. Diện tích hình chiếu của một đa giác
Cho đa giác ℋ nằm trong mặt phẳng (α) có diện tích là S và ℋ’ là hình chiếu vuông góc của ℋ trên mặt phẳng (β). Khi đó diện tích S’ của hình ℋ được tính theo công thức như sau:
S’ = S . cos φ
với φ là góc giữa (α) và (β).
Lý thuyết hai mặt phẳng vuông góc
Hai mặt phẳng được gọi là vuông góc với nhau nếu góc giữa hai mặt phẳng đó là góc vuông
Định lí 1. Điều kiện hai mặt phẳng vuông góc
Điều kiện cần và đủ để hai mặt phẳng vuông góc với nhau là mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.
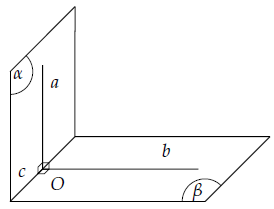
Hệ quả 1: Nếu hai mặt phẳng vuông góc với nhau thì bất cứ đường thẳng nào nằm trong mặt phẳng này và vuông góc với giao tuyến thì vuông góc với mặt phẳng kia.
Hệ quả 2: Cho hai mặt phẳng (α) và (β) vuông góc với nhau. Nếu từ một điểm thuộc mặt phẳng (α) ta dựng một đường thẳng vuông góc với mặt phẳng (β) thì đường thẳng này nằm trong mặt phẳng (α).
Định lí 2. Hai mặt phẳng cùng vuông góc với một mặt phẳng
Nếu hai mặt phẳng cắt nhau và cùng vuông góc với một mặt phẳng thì giao tuyến của chúng vuông góc với mặt phẳng đó.
Khái niệm các khối đa diện
1. Hình lăng trụ đứng
Hình lăng trụ đứng là hình lăng trụ có các cạnh bên vuông góc với đáy. Độ dài canh bên được gọi là chiều cao của hình lăng trụ đứng.
Nhận xét: Các mặt bên của hình lăng trụ đứng là hình chữ nhật và vuông góc với mặt đáy.
2. Hình lăng trụ đều
Hình lăng trụ đều là hình lăng trụ đứng có đáy là đa giác đều.
Nhận xét: Các mặt bên của hình lăng trụ đều là những hình chữ nhật bằng nhau và vuông góc với mặt đáy.
3. Hình hộp đứng
Hình hộp đứng là hình lăng trụ đứng có đáy là hình bình hành.
Nhận xét: Trong hình hộp đứng 4 mặt bên đều là hình chữ nhật.
4. Hình hộp chữ nhật
Hình hộp chữ nhật là hình hộp đứng có đáy là hình chữ nhật.
Nhận xét: Tất cả 6 mặt của hình hộp chữ nhật đều là hình chữ nhật.
5. Hình lập phương
Hình lập phương là hình hộp chữ nhật có tất cả các cạnh bằng nhau.
Nhận xét: Tất cả 6 mặt của hình lập phương đều là hình vuông.
6. Hình chóp đều
Một hình chóp được gọi là hình chóp đều nếu nó có đáy là một đa giác đều có chân đường cao trùng với tâm của đa giác đáy.
Nhận xét: Hình chóp đều có:
+) Các mặt bên là những tam giác cân bằng nhau. Các mặt bên tạo với mặt đáy các góc bằng nhau.
+) Các cạnh bên tạo với mặt đáy các góc bằng nhau.
7. Hình chóp cụt đều
Phần của hình chóp đều nằm giữa đáy và một thiết diện song song với đáy cắt các cạnh bên của hình chóp đều được gọi là hình chóp cụt đều.
Nhận xét: Hình chóp cụt đều có:
+) Hai đáy là hai đa giác đều và đồng dạng với nhau.
+) Các đường thẳng chứa các cạnh bên đồng quy tại một điểm.
+) Các mặt bên là các hình thang cân bằng nhau.
Dạng 1: Tìm góc giữa hai mặt phẳng
Phương pháp giải
Muốn tìm góc giữa hai mặt phẳng ta có: thể tìm góc giữa hai nửa đường thẳng lần lượt nằm trên hai mặt phẳng và vuông góc với giao tuyến của chúng.
Một số trường hợp thường gặp:
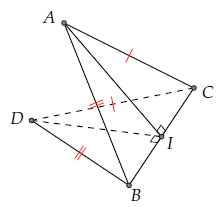
TH1: ∆ABC = ∆DBC. Gọi I là chân đường cao của ∆ABC.
Nối DI. Vì ∆ABC = ∆DBC nên DI ⊥ BC.
⇒
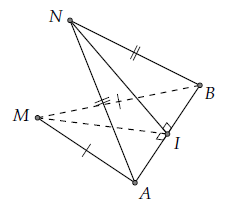
TH2: Xét góc giữa hai mặt phẳng (MAB) và (NAB) với ∆MAB và ∆NAB cân có cạnh đáy AB.
Gọi I là trung điểm AB. Khi đó: NI ⊥ AB và MI ⊥ AB.
⇒
TH3: Hai mặt phẳng cắt nhau (α) ∩ (β) = ∆.
Tìm giao tuyến ∆ của hai mặt phẳng.
Dựng AB có hai đầu mút nằm ở trên hai mặt phẳng và vuông góc với một mặt (giả sử là (β)).
Chiếu vuông góc của A hoặc B lên ∆ là điểm I.
⇒ là góc giữa hai mặt phẳng.
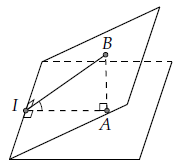
TH4: Nếu a ⊥ (α); b ⊥ (β) thì .
TH5: Trường hợp khó vẽ được góc giữa hai mặt phẳng thì có thể dùng công thức phép chiếu diện tích đa giác.
Bài tập vận dụng
Câu 1. Cho tứ diện S.ABC có đáy ABC là tam giác đều cạnh a, SA ⊥ (ABC) và . Tính góc giữa hai mặt phẳng (SBC) và (ABC).
Lời giải
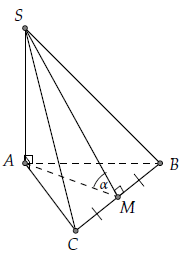
Gọi góc giữa hai mặt phẳng (SBC) và (ABC) là α.
Gọi M là trung điểm của BC. Do ∆ABC đều nên AM ⊥ BC (1)
Theo giả thiết SA ⊥ (ABC), suy ra theo (1) ta có SM ⊥ BC (2)
Lại có: (SBC) ∩ (ABC) = BC (3)
Từ (1), (2) và (3) ta có:
Ta có:
Xét tam giác SAM vuông tại A, ta có:
, suy ra: α = 60°.
Câu 2. Cho hình vuông ABCD cạnh a, SA ⊥ (ABCD) và . Tính số đo của góc giữa các mặt phẳng sau:
a) ((SBC), (ABC)) = ?
b) ((SBD), (ABD)) = ?
c) ((SAB), (SCD)) = ?
Lời giải
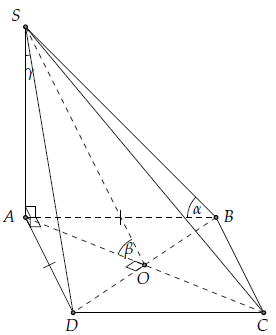
a) Gọi α = (S, BC, A).
Khi đó ta có:
Suy ra:
Trong ∆SAB có:
b) Gọi β = (S, BD, A) và AC ∩ BD = O, ta có:
Mà: suy ra:
c) Gọi γ = ((SAB), (SCD)).
Khi đó ta có: và
Câu 3. Cho tứ diện S.ABC có , AB = 2a;
, SA ⊥ (ABC); SA = 2a. Gọi M là trung điểm AB. Hãy tính:
a)
b) Đường cao AH của ∆AMC.
c)
Lời giải.
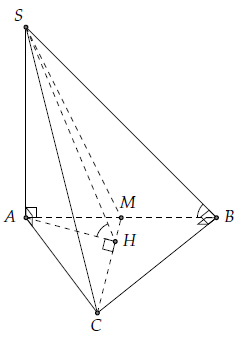
a) Gọi
Trong tam giác ABC ta có: AB ⊥ BC và SB ⊥ BC
Suy ra:
Ta có: AB = SA = 2a nên suy ra: α = 45°.
b) Đường cao AH của ∆AMC.
Ta có: và
Do đó:
c) Gọi ?
Do
Trong ∆SHA có:
Câu 4. Trong mặt phẳng (P) cho một ABC vuông cân, cạnh huyền BC = a. Trên nửa đường thẳng vuông góc với (P) tại A lấy điểm S.
a) Tính góc giữa hai mặt phẳng ((SAB), (CAB)) và ((SAC), (BAC)) và ((CSA), (BSA)).
b) Tính SA để góc giữa hai mặt phẳng ((SBC), (ABC)) có số đo 30°.
Lời giải.
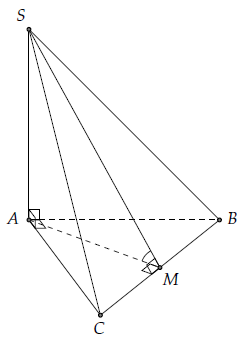
a) Dễ thấy (SAB) ⊥ (ABC), (SAB) ⊥ (SAC), (ABC) ⊥ (SAC)
Do đó các góc giữa các mặt phẳng ((SAB), (CAB)) và ((SAC), (BAC)) và ((CSA), (BSA)) đều bằng 90◦.
b) Gọi α là góc giữa hai mặt phẳng ((SBC), (ABC)).
Gọi M là trung điểm cạnh BC, khi đó ta có:
Ta có: , theo đề thì
Câu 5. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, , SA ⊥ (ABCD).
a) Tính góc giữa hai mặt phẳng (SCD) và (ABCD) với SA = a.
b) Tìm x = SA để góc giữa hai mặt phẳng (SCD) và (ABCD) bằng 60°.
Lời giải.
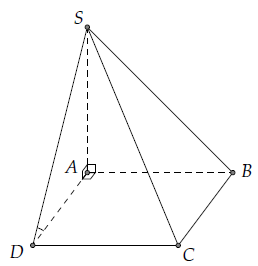
a) Vì SA ⊥ (ABCD) ⇒ CD ⊥ SA
Theo giả thiết CD ⊥ AD và (SCD) ∩ (ABCD) = CD
Suy ra: α = ((SCD), (ABCD)) = S’DA.
Xét tam giác SAD vuông tại A ta có:
b) Theo kết quả câu a ta có:
Câu 6. Cho tam giác vuông ABC có cạnh huyền BC nằm trên mặt phẳng (P). Gọi α, β lần lượt là góc hợp bởi hai đường thẳng AB, AC và mặt phẳng (P). Gọi φ là hợp bởi (ABC) và (P). Chứng minh rằng sin2 φ = sin2 α + sin2 β.
Lời giải.
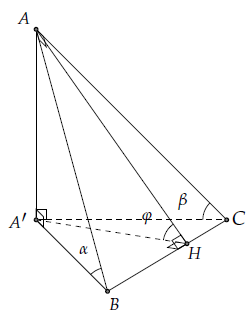
Gọi A’ là hình chiếu vuông góc của A lên mặt phẳng (P), AH là đường cao của tam giác ABC.
Suy ra: A’B và A’C lần lượt là hình chiếu của AB và AC lên mặt phẳng (P).
Do đó: và
Lại có:
Xét tam giác ABC vuông tại A, ta có:
Câu 7. Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. Gọi α, β, φ lần lượt là góc hợp bởi các mặt phẳng (OBC), (OCA), (OAB) với mặt phẳng (ABC). Chứng minh rằng cos2α + cos2 β + cos2 φ = 1.
Lời giải.
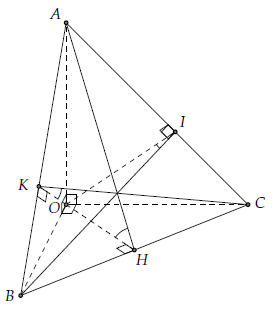
Gọi OH, OK, OI lần lượt là các đường cao của các tam giác OBC, OAB, OAC.
Ta có:
Ta có:
Ta có:
Do đó:
Suy ra điều phải chứng minh.
Dạng 2: Tính diện tích hình chiếu của đa giác
Phương pháp giải
Gọi S là diện tích của đa giác H trong (P), S’ là diện tích của hình chiếu H’ của H trên (Q), và . Khi đó: S’ = S . cos φ
Bài tập vận dụng
Câu 1. Cho ∆ABC cân tại A, đường cao , BC = 3a có BC nằm trong (P). Gọi A’ là hình chiếu của A lên (P). Khi ∆A’BC vuông tại A’, tính
.
Lời giải
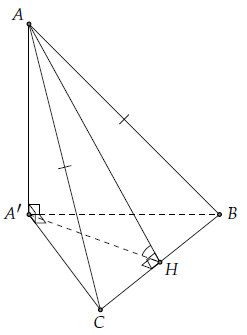
Gọi M là trung điểm của cạnh BC.
Do ∆ABC cân tại A nên AM ⊥ BC.
Mặt khác: AA’ ⊥ (P) ⇒ A’H ⊥ BC. Do đó:
Theo đề ta có:
Lại có:
Suy ra:
Khi đó ta có:
Suy ra: α = 30°.
Câu 2. Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, và SA ⊥ (ABC). Tính diện tích tam giác SBC.
Lời giải.
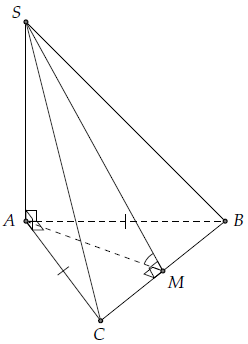
Gọi M là trung điểm cạnh BC.
Dễ dàng chứng minh được là góc giữa hai mặt phẳng (ABC) và (SBC).
Mặt khác: SA ⊥ (ABC),
Suy ra: ∆ABC là hình chiếu của ∆SBC lên mặt phẳng (ABC).
Do đó:
Lại có: và
Xét tam giác SAM vuông tại A, ta có:
Thay vào (1) ta được:
Câu 3. Cho hình thoi ABCD có đỉnh A nằm trong (P) các đỉnh còn lại không nằm trong (P), BD = a, . Chiếu vuông góc hình thoi ABCD lên (P), ta được hình vuông AB’C’D’.
a) Tính SABCD và SAB’C’D’ từ đó suy ra
b) Gọi E, F lần lượt là giao điểm của CB và CD với (P). Tính SEFDB; SEFD’B’.
Lời giải.
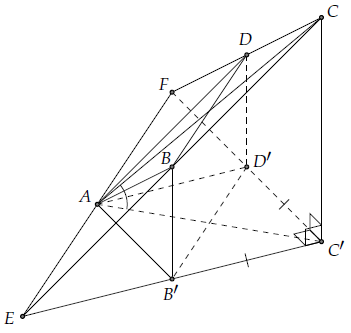
a) Ta có:
Do AB’C’D’ là hình chiếu của ABCD lên (P) và BD // B’D’ nên BD = B’D’ = a.
Mà: AB’C’D’ là hình vuông nên suy ra
Do đó:
Mặt khác: SAB’C’D’ = SABCD . cos α
⇒
b) Trong mặt phẳng (CC’D’D) gọi F là giao điểm của CD và C’D’
Trong mặt phẳng (BB’C’C) gọi E là giao điểm của BC và B’C’.
Dễ thấy:
⇒ FE // BD // B’D’
Suy ra: BDFE và B’D’FE là các hình thang cân.
Lại có: AD // BE ⇒ ADBE là hình bình hành.
Tương tự cũng có ABDF cũng là hình bình hành.
Suy ra: EF = 2B’D’ = 2a. Do đó:
Mà: SEFD’B’ = SEFDB . cos φ
⇒
Dạng 3: Chứng minh hai mặt phẳng vuông góc
Phương pháp giải
Cách 1: Chứng minh mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia
Cách 2: Chứng minh góc giữa hai mặt phẳng bằng 90°.
Bài tập vận dụng
Câu 1. Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA ⊥ (ABCD). Chứng minh rằng:
a) (SAC) ⊥ (SBD)
b) (SAB) ⊥ (SBC)
Lời giải
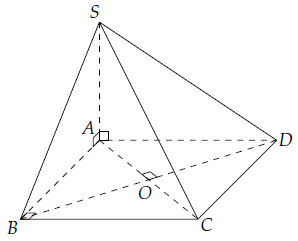
a) Ta có: AC ⊥ BD, AC ⊥ SA (vì SA ⊥ (ABCD)).
Do đó AC ⊥ (SBD).
Vì vậy (SAC) ⊥ (SBD).
b) Ta có: BC ⊥ AB, BC ⊥ SA (vì SA ⊥ (ABCD)).
Do đó BC ⊥ (SBD).
Vì vậy (SBC) ⊥ (SAB).
Câu 2. Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA ⊥ (ABCD). Gọi M và N lần lượt là hình chiếu của A lên SB và SD. Chứng minh rằng (SAC) ⊥ (AMN)
Lời giải
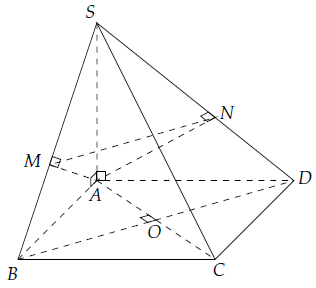
Ta có: BD ⊥ AC, BD ⊥ SA (vì SA ⊥ (ABCD)).
Do đó: BD ⊥ (SAC).
Mà MN // BD do
Nên MN ⊥ (SAC).
Vì vậy (SAC) ⊥ (AMN).
Câu 3. Cho hình chóp S.ABC có tam giác ABC vuông tại A, SA ⊥ (ABC). Gọi H và K lần lượt là hình chiếu của B trên các đường thẳng SA và SC. Chứng minh rằng:
a) (SAC) ⊥ (SAB)
b) (SAC) ⊥ (BHK)
Lời giải
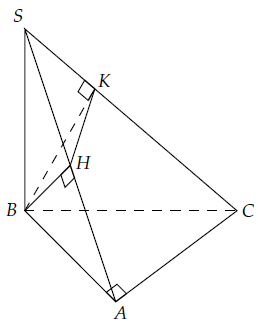
a) Ta có: AC ⊥ AB, AC ⊥ SA (vì SA ⊥ (ABC)).
Do đó AC ⊥ (SAB).
Vì vậy (SAC) ⊥ (SAB).
b) Ta có: SC ⊥
Mặt khác: BH ⊥ SA và BH ⊥ AC (vì AC ⊥ (SAB)).
Do đó: BH ⊥ (SAC)
Suy ra: SC ⊥ BH.
Từ đó: SC ⊥ (BHK).
Vì vậy (SAC) ⊥ (BHK).
Câu 4. Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O với AB = a, , SO ⊥ (ABCD), SB = a. Chứng minh rằng (SAB) ⊥ (SAD).
Lời giải
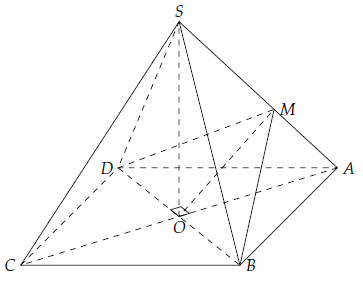
Gọi M là hình chiếu của O lên SA.
Khi đó: SA ⊥ (MBD).
Do đó góc giữa hai mặt phẳng (SAB) và (SAD) chính là góc giữa hai đường thẳng MB và MD.
Ta có:
Suy ra:
Vì thế tam giác MBD vuông cân tại M, từ đó hay (SAB) ⊥ (SAD).
Câu 5. Cho hình chóp S.ABCD có đáy ABCD là hình thoi và SA = SB = SC. Chứng minh rằng (SBD) ⊥ (ABCD).
Lời giải.
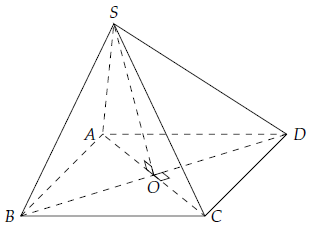
Ta có: AC ⊥ BD.
Gọi O là tâm hình thoi ABCD.
Vì SA = SC nên AC ⊥ SO.
Do đó: AC ⊥ (SBD).
Vì vậy (ABCD) ⊥ (SBD).
Câu 6. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA = 2a, SA ⊥ (ABC). Gọi I là trung điểm của BC. Chứng minh rằng (SAI) ⊥ (SBC).
Lời giải.
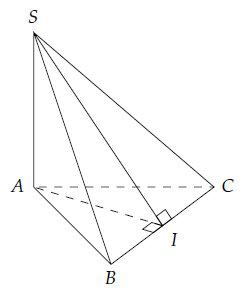
Ta có: SA ⊥ (ABC) nên BC ⊥ SA.
Vì AB = AC nên BC ⊥ AI.
Do đó: BC ⊥ (SAI).
Vì vậy (SBC) ⊥ (SAI).
Câu 7. Trong mặt phẳng (P) cho hình vuông ABCD. Gọi S là một điểm không thuộc (P) sao cho
SAB là tam giác đều và (SAB) ⊥ (ABCD). Chứng minh rằng (SAD) ⊥ (SAB).
Lời giải.
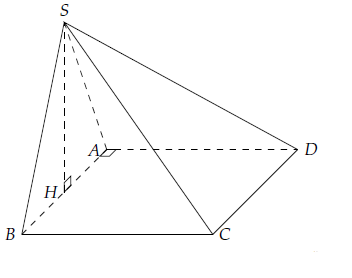
Gọi H là trung điểm AB.
Ta có: SAB là tam giác đều nên SH ⊥ AB.
Mà: (SAB) ⊥ (ABCD) nên SH ⊥ (ABCD).
Suy ra: AD ⊥ SH.
Mặt khác: AD ⊥ AB.
Do đó: AD ⊥ (SAB).
Từ đó: (SAD) ⊥ (SAB).
Câu 8. Cho hình lăng trụ đứng ABC.A’B’C’ có AB = AC = a, . Gọi M là trung điểm của AC. Chứng minh rằng (BC’M) ⊥ (ACC’A’).
Lời giải.
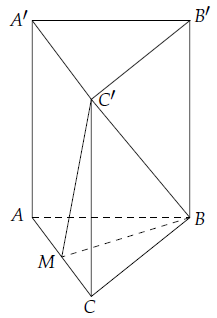
Vì AB = AC nên BM ⊥ AC.
ABC.A’B’C’ là lăng trụ đứng nên BM ⊥ AA’.
Do đó: BM ⊥ (ACC’A’).
Vì vậy: (BC’M) ⊥ (ACC’A’).
Câu 9. Cho hình chóp S.ABC có SA ⊥ (ABC). Gọi H và K lần lượt là trực tâm các tam giác ABC và SBC. Chứng minh rằng (SBC) ⊥ (CHK).
Lời giải.
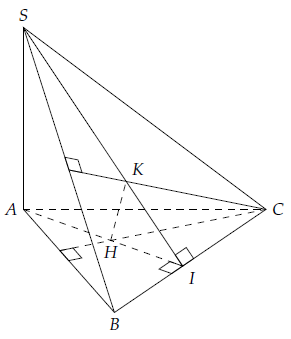
Gọi I = AH ∩ BC. Khi đó: BC ⊥ (SAI)
Suy ra: BC ⊥ SI.
Do đó: S, K, I thẳng hàng.
Ta có: SB ⊥ CK.
Mặt khác: CH ⊥ AB, CH ⊥ SA suy ra: CS ⊥ (SAB).
Từ đó: SB ⊥ SH.
Do đó: SB ⊥ (CHK).
Vì vậy: (SBC) ⊥ (CHK).
Câu 10. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a, , SA ⊥ (ABCD). Gọi M là trung điểm AD. Chứng minh rằng (SAC) ⊥ (SMB).
Lời giải.
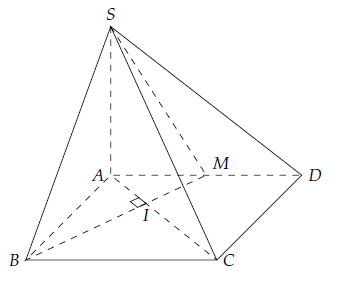
Gọi I = AC ∩ BM.
Vì SA ⊥ (ABCD) nên BM ⊥ SA.
Theo giả thiết ta suy ra:
Do đó: AI2 + MI2 = MA2.
Từ đó: BM ⊥ AC.
Suy ra: BM ⊥ (SAC). Vì vậy (SBM) ⊥ (SAC).
Câu 11. Cho hình vuông ABCD và tam giác đều SAB cạnh a nằm trong hai mặt phẳng vuông góc
nhau. Gọi I và F lần lượt là trung điểm AB và AD. Chứng minh rằng (SID) ⊥ (SFC).
Lời giải.
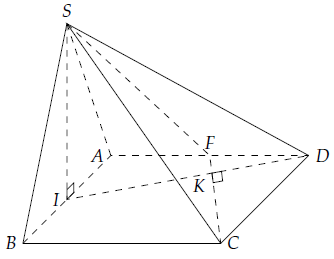
Gọi K = CF ∩ ID.
Tam giác SAB đều nên SI ⊥ AB.
Mà: (SAB) ⊥ (ABCD) nên SI ⊥ (ABCD), suy ra: CF ⊥ SI.
Mặt khác:
Suy ra: CF ⊥ ID. Do đó CF ⊥ (SID).
Vì vậy: (SFC) ⊥ (SID).
Dạng 4: Thiết diện chứa một đường thẳng và vuông góc với mặt phẳng.
Phương pháp giải
Xác định mặt phẳng (β) chứa đường thẳng d và vuông góc với mặt phẳng (α) cho trước bằng cách:
a) Từ điểm A bất kì thuộc đường thẳng d và dựng AH ⊥ (α). Mặt phẳng (AH, d) là mặt phẳng (β)
b) Tìm giao điểm của mặt phẳng (β) và các cạnh của hình chóp, hình lăng trụ… Từ đó suy ra: thiết diện.
Bài tập vận dụng
Câu 1. Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA vuông góc với mặt đáy. Gọi (P) là mặt phẳng chứa AD và vuông góc với mặt phẳng (SBC). Xác định thiết diện do mặt phẳng (P) cắt hình chóp.
Lời giải
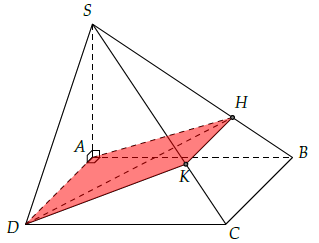
Kẻ AH ⊥ SB (H ∈ SB).
Ta có:
⇒ AD ⊥ (SAB) ⇒ AD ⊥ SB.
Ta có: AD ⊥ SB và AH ⊥ SB nên SB ⊥ (ADH)
Suy ra: (SBC) ⊥ (ADH).
Do đó, mặt phẳng (P) chứa AD và vuông góc với mặt phẳng (SBC) là (ADH).
Trong mặt phẳng (SBC) dựng HK ∥ BC (K ∈ BC).
Suy ra: HK ∥ AD (do cùng song song với AD).
Vậy thiết diện là hình thang ADKH có hai đáy là AD và HK.
Câu 2. Cho tứ diện OABC có các cạnh OA, OB, OC đôi một vuông góc nhau và OA = OB = OC = a. Gọi M là điểm trên AC sao cho AC = 3MC. Gọi H là hình chiếu của O lên mặt phẳng (ABC). Gọi (α) là mặt phẳng chứa OM và vuông góc với mặt phẳng (ABC). Xác định và tính diện tích thiết diện do mặt phẳng (α) cắt tứ diện.
Lời giải
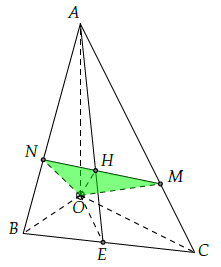
Ta có: OA ⊥ OB và OA ⊥ OC nên OA ⊥ (OBC).
Vì: OH ⊥ BC (do OH ⊥ (ABC)) và OA ⊥ BC (do OH ⊥ (ABC))
Nên: BC ⊥ (OAH)
Suy ra: BC ⊥ AH (1).
Tương tự ta có: AC ⊥ BH(2).
Từ (1) và (2) suy ra: H là trực tâm của ∆ABC.
Ta có: OH ⊥ (ABC) nên mặt phẳng (α) chứa OM và vuông góc với mặt phẳng (ABC) là (OHM).
Trong mặt phẳng (ABC) gọi N là giao điểm của HM và AB
Suy ra thiết diện của mặt phẳng (OHM) và tứ diện là ∆OMN.
Do OA = OB = OC = a và OA, OB, OC đôi một vuông góc nhau nên
Suy ra ∆ABC đều.
Mà: H là trực tâm của ∆ABC nên AH cắt BC tại trung điểm của đoạn BC.
Gọi E là trung điểm BC.
Ta có: H là trọng tâm ∆ABC nên 3HE = AE.
Do đó: MN ∥ BC, suy ra:
Vì ∆AOE vuông tại A nên:
Suy ra:
Vậy:
Câu 3. Cho hình chóp S.ABCD có đáy ABCD là hình vuông có tâm O, cạnh a, SA vuông góc với mặt đáy và SA = 2a. Gọi I là trung điểm của SB, (α) là mặt phẳng chứa OI và vuông góc với mặt phẳng (ABCD). Xác định và tính diện tích thiết diện do mặt phẳng (α) cắt hình chóp.
Lời giải.
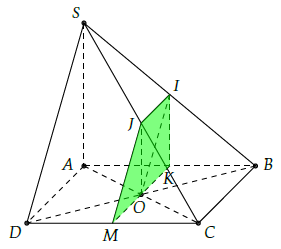
Trong (SAC) kẻ OJ ∥ SA (J ∈ SC) ⇒ J là trung điểm SC.
Ta có: OJ ⊥ (ABCD). Mặt phẳng (α) là (OIJ).
Gọi K là trung điểm AB.
Trong (ABCD) gọi M là giao điểm của OK và CD.
Thiết diện là hình thang I JMK vuông tại I và K.
Câu 3. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, AD = 2a, AB = BC = a, SA vuông góc với đáy, . Gọi E là trung điểm BC. Xác định và tính diện tích thiết diện của mặt phẳng chứa SE và vuông góc với mặt phẳng (SAC) với hình chóp.
Lời giải.
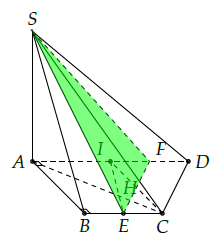
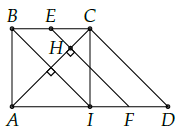
Gọi I là trung điểm của AD ⇒ ABCI là hình vuông ⇒ AC ⊥ BI (1).
Ta có: BCDI là hình bình hành ⇒ BI ∥ CD (2).
Từ (1) và (2 suy ra: AC ⊥ CD.
Ta có: CD ⊥ (SAC).
Kẻ EF ∥ CD (F ∈ AD).
Suy ra: EF ⊥ (SAC) ⇒ (SEF) ⊥ (SAC).
Mặt phẳng chứa SE và vuông góc (SAC) là mặt phẳng (SEF).
Thiết diện của mặt phẳng (SEF) với hình chóp là tam giác SEF.
Gọi H = AC ∩ EF.
Ta có: EF ⊥ SH.
Ta có: EFDC là hình bình hành
Vậy:
Câu 4. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại C, SA ⊥ (ABC), SA = AC = a. Gọi I lần lượt là trung điểm của SB. Lấy điểm M trên cạnh AC sao cho 3AM = AC. Gọi (α) là mặt phẳng chứa IM và vuông góc với mặt phẳng (SAC). Xác định và tính diện tích thiết diện của mặt phẳng (α) và hình chóp.
Lời giải.
Trong mặt phẳng (ABC), kẻ MN ∥ BC (N ∈ AB).
Ta có: BC ⊥ (SAC).
Mà MN ǁ BC nên MN ⊥ (SAC).
Suy ra: (IMN) ⊥ (SAC).
Mặt phẳng chứa IM và vuông góc với mặt phẳng (SAC) là mặt phẳng (IMN).
Gọi J là trung điểm SC. Ta có: IJ ∥ MN.
Suy ra: thiết diện cắt bởi (IMN) và hình chóp là hình thang IJMN vuông tại M và J.
Ta có:
Vậy:
Câu 5. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AB = 2a, AD = CD = SA = a, SA vuông góc với đáy. Gọi I, M lần lượt là trung điểm SB, AD. Gọi (P) là mặt phẳng chứa IM và vuông góc (SAD). Tính diện tích thiết diện do (P) cắt hình chóp.
Lời giải
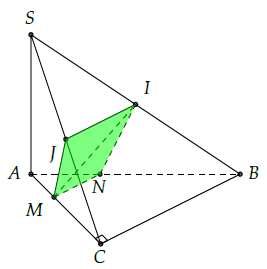
Gọi N là trung điểm BC.
Ta có: MN ∥ AB ∥ CD và MN ⊥ AD.
Ta có: MN ⊥ (SAD) ⇒ (IMN) ⊥ (SAD).
Mặt phẳng (P) là (IMN).
Kẻ IK ∥ AB(K ∈ SA).
Thiết diện là hình thang IKMN vuông tại K và M.
Suy ra:
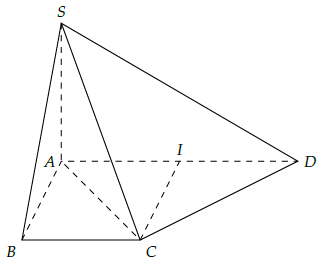
Câu 6. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, AB = BC = a, AD = 2a, SA ⊥ (ABCD). Chứng minh rằng (SAC) ⊥ (SCD).
Lời giải.
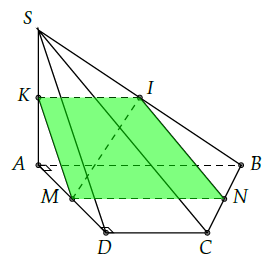
Vì SA ⊥ (ABCD) nên CD ⊥ SA.
Gọi I là trung điểm AD.
Khi đó: ABCI là hình vuông và tam giác ICD vuông cân tại I.
Từ đó A’CD = 90° hay CD ⊥ AC
Do đó CD ⊥ (SAC). Vì vậy (SCD) ⊥ (SAC).
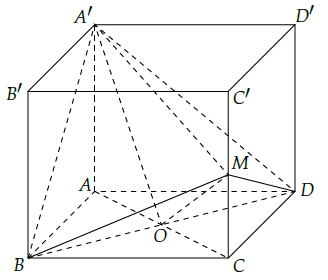
Câu 7. Cho hình hộp chữ nhật ABCD.A’B’C’D’ có đáy là hình vuông ABCD cạnh a, AA’ = b. Gọi M là trung điểm của CC’. Xác định tỉ số để hai mặt phẳng (A’BD) và (MBD) vuông góc với nhau.
Lời giải.
Gọi O là tâm ABCD.
Vì A’B = A’D nên A’O ⊥ BD.
Vì MB = MD nên MO ⊥ BD.
Suy ra: góc giữa (A’BD) và (MBD) là góc giữa A’O và MO.
Do đó (A’BD) ⊥ (MBD) khi:
Ta có:
Vì vậy để (A’BD) ⊥ (MBD) thì:
Vậy: thì (A’BD) ⊥ (MBD).
Câu 8. Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác vuông cân tại B và . Gọi M, N lần lượt là trung điểm AC, AA’. Gọi I, J lần lượt là trung điểm AB, CM.
a) Chứng minh (AC’B) ⊥ (BMN).
b) Xác định thiết diện do mặt phẳng (P) chứa IJ và vuông góc (BMN) với hình lăng trụ.
Lời giải
a) Ta có: và
Suy ra: AA’C’C là hình vuông.
Do đó: AC’ ⊥ A’C.
Mà: MN ∥ A’C nên MN ⊥ AC’ (1)
Ta có: BM ⊥ AC (do OABC vuông cân tại B và M là trung điểm AC)
Và BM ⊥ AA’ (do AA’ ⊥ (ABC).
Suy ra: BM ⊥ (AA’C’C).
Do đó BM ⊥ AC’ (2)
Từ (1) và (2) suy ra: AC’ ⊥ (BMN).
Vậy (AC’B’) ⊥ (BMN).
b) Kẻ JK ∥ AC’ (K ∈ CC’).
Ta có: JK ⊥ (BMN).
Suy ra: (IJK) ⊥ (BMN). Mặt phẳng (α) là (IJK).
Trong (ABC) gọi D = I J ∩ BC, trong (BB’C’C) gọi E = DK ∩ BB .
Thiết diện là tứ giác IJKE.
Bạn đang xem bài viết Lý thuyết và 4 dạng bài tập xem thêm các bài viết khác về chủ đề Toán lớp 11. Chúc bạn 1 ngày vui vẻ!