Bạn đang xem bài viết Lý thuyết và các dạng bài tập phổ biến. Hi vọng sẽ là đáp án bạn ưng ý. Cùng theo dõi nhé!
Cấp số cộng là điểm kiến thức nền tảng trong phần dãy số bên cạnh cấp số nhân. Bài viết dưới đây, Cấp Nước Lào Cai sẽ giúp bạn đọc tìm hiểu chi tiết lý thuyết cấp số cộng và một vài dạng bài tập đặc trưng.
Lý thuyết cấp số cộng
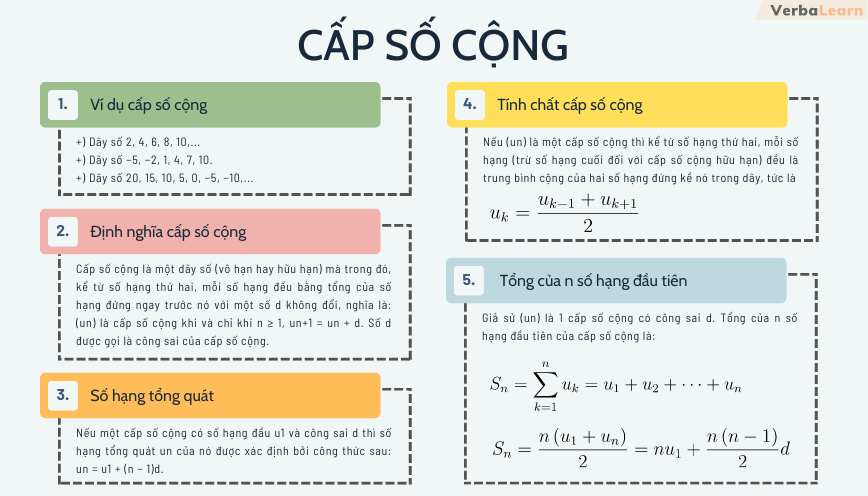
1. Ví dụ cấp số cộng
+) Dãy số 2, 4, 6, 8, 10,…
+) Dãy số −5, −2, 1, 4, 7, 10.
+) Dãy số 20, 15, 10, 5, 0, −5, −10,…
2. Định nghĩa cấp số cộng
Cấp số cộng là một dãy số (vô hạn hay hữu hạn) mà trong đó, kể từ số hạng thứ hai, mỗi số hạng đều bằng tổng của số hạng đứng ngay trước nó với một số d không đổi, nghĩa là: (un) là cấp số cộng khi và chỉ khi n ≥ 1, un+1 = un + d. Số d được gọi là công sai của cấp số cộng.
Để chứng minh một dãy số (un) là một cấp số cộng, ta xét hiệu un+1 − un = d (không đổi) với mọi n ∈ ℕ*.
3. Tính chất cấp số cộng
Tính chất 1. Nếu (un) là một cấp số cộng thì kể từ số hạng thứ hai, mỗi số hạng (trừ số hạng cuối đối với cấp số cộng hữu hạn) đều là trung bình cộng của hai số hạng đứng kề nó trong dãy, tức là .
4. Hệ quả
Ba số a, b, c (theo thứ tự đó) lập thành một cấp số cộng khi và chỉ khi a + c = 2b.
5. Số hạng tổng quát của cấp số cộng
Nếu một cấp số cộng có số hạng đầu u1 và công sai d thì số hạng tổng quát un của nó được xác định bởi công thức sau: un = u1 + (n − 1)d.
Chú ý:
Để tìm n số hạng liên tiếp của cấp số cộng thỏa điều kiện, ta cần nhớ:
+) Nếu n lẻ, cần đặt số hạng cần tìm là x, công sai: d.
+) Nếu n chẵn, cần đặt số hạng cần tìm là x − d, công sai: 2d.
6. Tổng của n số hạng đầu tiên của cấp số cộng
Giả sử (un) là 1 cấp số cộng có công sai d.
Gọi (Sn là tổng n số hạng đầu tiên của cấp số cộng). Ta có:
Phân dạng bài tập cấp số cộng
Câu 1. Chứng minh các dãy số sau là một cấp số cộng. Xác định công sai và số hạng đầu tiên của cấp số cộng đó?
a) Dãy số (un) với un = 19n − 5.
ĐS: d = 19, u1 = 14
b) Dãy số (un) với un = −3n + 1.
ĐS: d = −3, u1 = −2
Lời giải
a) Ta có: un+1 − un
= 19(n + 1) − 5 − 19n + 5
= 19n + 19 − 5 − 19n + 5 = 19.
Do đó dãy số (un) là một cấp số cộng với công sai d = 19, số hạng đầu u1 = 14.
b) Ta có: un+1 − un
= −3(n + 1) + 1 + 3n − 1
= −3n − 3 + 1 + 3n − 1 = −3.
Do đó dãy số (un) là một cấp số cộng với công sai d = −3, số hạng đầu u1 = −2.
Câu 2. Ba góc của một tam giác vuông lập thành một cấp số cộng. Tìm ba góc đó.
ĐS:
Lời giải
Gọi ba góc của tam giác lần lượt là A, B, C.
Khi đó ta có: A + B + C = π.
Do ba góc A, B, C của tam giác theo thứ tự lập thành một cấp số cộng nên A + C = 2B.
Do đó:
Do tam giác ABC vuông nên giả sử , khi đó công sai d của cấp số cộng là
.
Vậy góc A của tam giác là
Câu 3. Một tam giác vuông có chu vi bằng 12 cm và ba cạnh lập thành một cấp số cộng. Tính độ dài ba cạnh của tam giác đó.
ĐS: 5cm, 4cm, 3cm
Lời giải
Giả sử ba cạnh của tam giác vuông lần lượt là a, b, c trong đó a là cạnh huyền và a > b > c.
Do tam giác vuông có chu vi bằng 12 cm nên a + b + c = 12.
Mặt khác a, b, c theo thứ tự lập thành cấp số cộng nên a + c = 2b.
Khi đó: 2b + b = 12
⇔ 3b = 12 ⇔ b = 4cm.
Giả sử công sai của cấp số cộng là d thì a = 4 − d, c = 4 + d.
Do tam giác vuông cạnh huyền là a nên a2 = b2 + c2
⇔ (4 − d)2 = 42 + (4 + d)2
⇔ −16d = 16 ⇔ d = −1.
Vậy: a = 5cm, c = 3cm.
Câu 4. Một cấp số cộng có 10 số hạng, trong đó số hạng đầu bằng 5, số hạng cuối bằng 23. Tìm cấp số cộng đó?
ĐS: 5, 7, 9, 11, 13, 15, 17, 19, 21, 23
Lời giải
Ta có: u10 = u1 + 9d
⇔ 23 = 5 + 9d ⇔ d = 2.
Vậy cấp số cộng cần tìm là 5, 7, 9, 11, 13, 15, 17, 19, 21, 23.
Câu 5. Tìm ba số hạng liên tiếp của một cấp số cộng biết tổng của chúng bằng 27 và tổng các bình phương của chúng là 293.
ĐS: 4, 9, 14
Lời giải
Gọi ba số hạng liên tiếp của cấp số cộng là x − d, x, x + d trong đó d là công sai của cấp số cộng.
Khi đó ta có: x − d + x + x + d = 27
⇔ 3x = 27 ⇔ x = 9.
Mà: (x − d)2 + x2 + (x + d)2 = 293
⇔ (9 − d)2 + 81 + (9 + d)2 = 293
⇔ 2d2 − 50 = 0
⇔ d = 5 ∨ d = −5.
Với d = 5 thì ba số hạng của cấp số cộng là 4, 9, 14.
Với d = −5 thì ba số hạng của cấp số cộng là 14, 9, 4.
Vậy ba số hạng liên tiếp của cấp số cộng là 4, 9, 14.
Câu 6. Tìm bốn số hạng liên tiếp của một cấp số cộng, biết tổng của chúng bằng 10 và tổng bình phương của chúng bằng 30.
ĐS: 1, 2, 3, 4
Lời giải
Gọi bốn số hạng liên tiếp của cấp số cộng là x − 3d, x − d, x + d, x + 3d với 2d là công sai của cấp số cộng.
Khi đó ta có:
x − 3d + x − d + x + d + x + 3d = 10
⇔ 4x = 10
⇔ x =
Mặt khác:
(x − 3d)2 + (x − d)2 + (x + d)2 + (x + 3d)2 = 30
⇔ 4x2 + 20d2 = 30
⇔ d2 =
⇔ d = ∨ d =
Với x = thì d =
, khi đó bốn số hạng liên tiếp của cấp số cộng là 1, 2, 3, 4.
Với x = thì d =
, khi đó bốn số hạng liên tiếp của cấp số cộng là 4, 3, 2, 1.
Vậy bốn số hạng liên tiếp của cấp số cộng là 1, 2, 3, 4.
Câu 7. Cho một cấp số cộng (un) có u3 + u28 = 100. Hãy tính tổng của 30 số hạng đầu tiên của cấp số cộng đó.
ĐS: 1500
Lời giải
Ta có:
Câu 8. Cho một cấp số cộng (un) có S6 = 18 và S10 = 110. Tính S20.
ĐS: S20 = 620
Lời giải
Giả sử cấp số cộng (un) có số hạng đầu là u1 và công sai là d.
Ta có:
Từ (1) và (2), ta có hệ phương trình:
Khi đó:
Câu 9. Tính các tổng sau:
a) S = 1 + 3 + 5 + ··· + (2n − 1) + (2n + 1).
ĐS: S = (n + 1)2
b) S = 1002 − 992 + 982 − 972 + ··· + 22 − 12.
ĐS: S = 5050
Lời giải
a) S = 1 + 3 + 5 + ··· + (2n − 1) + (2n + 1)
Xét cấp số cộng (uk), k ∈ ℕ* với số hạng đầu là u1 = 1 và công sai là d = 2.
Ta có: uk = u1 + (k − 1)d
⇔ 2n + 1 = 1 + 2(k − 1)
⇔ k = n + 1.
Vậy:
b) S = 1002 − 992 + 982 − 972 + ··· + 22 − 12 = 199 + 195 + ··· + 3
Xét cấp số cộng (un) có số hạng đầu u1 = 199 và công sai d = u2 − u1 = 195 − 199 = −4.
Ta có: un = u1 + (n − 1)d
⇔ 3 = 199 − 4(n − 1) ⇔ n = 50.
Khi đó:
Câu 10. Tìm số hạng đầu tiên, công sai, số hạng thứ 20 và tổng của 20 số hạng đầu tiên của các cấp số cộng sau, biết rằng:
a)
ĐS: u1 = 3, d = 4, u20 = 79, S20 = 820
b)
ĐS: u1 = 1, d = 3, u20 = 58, S20 = 590
c)
ĐS: u1 = , d =
, u20 = 31, S20 = 335
d)
ĐS: u1 = 3, d = 1, u20 = 22, S20 = 250
Hoặc u1 = −11, d = , u20 =
, S20 = 502
Lời giải.
a)
Vậy số hạng đầu của cấp số cộng là u1 = 3, công sai là d = 4.
Khi đó số hạng thứ 20 là:
u20 = u1 + 19d = 3 + 19⋅4 = 79.
Tổng của 20 số hạng đầu tiên của cấp số cộng là
b)
Vậy số hạng đầu của cấp số cộng là u1 = 1, công sai là d = 3.
Khi đó số hạng thứ 20 là:
u20 = u1 + 19d = 1 + 19⋅3 = 58.
Tổng của 20 số hạng đầu tiên của cấp số cộng là:
c)
Vậy số hạng đầu của cấp số cộng là u1 = , công sai là d =
.
Khi đó số hạng thứ 20 là:
u20 = u1 + 19d = + 19⋅
= 31.
Tổng của 20 số hạng đầu tiên của cấp số cộng là:
d)
Từ (1), ta có u1 + 5d = 8 ⇔ u1 = 8 − 5d, thay vào (2)
(8 − 4d)2 + (8 − 2d)2 = 52
⇔ 20d2 − 96d + 76 = 0
⇔ d = 1 ∨ d =
+) Với d = 1 thì u1 = 3. Khi đó số hạng thứ 20 là:
u20 = u1 + 19d = 3 + 19⋅1 = 22.
Tổng của 20 số hạng đầu tiên của cấp số cộng là:
+) Với d = thì u1 = −11. Khi đó số hạng thứ 20 là:
u20 = u1 + 19d = −11 + 19⋅ =
Tổng của 20 số hạng đầu tiên của cấp số cộng là:
Câu 11. Tìm số hạng đầu và công sai của cấp số cộng, biết:
a)
ĐS: u1 = 3, d = 4
b)
ĐS: u1 = 3, d = 4
c)
ĐS: u1 = −5, d = 2 3
d)
ĐS:
e)
ĐS: Không tồn tại
f)
ĐS:
g)
ĐS: u1 = 1, d = 3
h)
ĐS:
i)
ĐS:
k)
ĐS:
l)
ĐS:
m)
ĐS:
n)
ĐS:
o)
ĐS:
Lời giải.
a)
Vậy số hạng đầu của cấp số cộng là u1 = 3, công sai là d = 4.
b)
Vậy số hạng đầu của cấp số cộng là u1 = 3, công sai là d = 4.
c)
Vậy số hạng đầu của cấp số cộng là u1 = –5, công sai là d = 2.
d)
Vậy số hạng đầu của cấp số cộng là u1 = 3, công sai là d = 2 hoặc u1 = –17, d = 2.
e)
Từ (1) suy ra d = 60 – 2u6, thay vào (2), ta có:
Vậy không tồn tại cấp số cộng thỏa yêu cầu bài toán.
f)
Từ (2), ta có 3u1 + 3d = 21 ⇒ d = 7 − u1, thay vào (1)
Với u1 = 9 thì d = –2.
Với u1 = 5 thì d = 2
Vậy số hạng đầu của cấp số cộng là u1 = 9, công sai là d = –2 hoặc u1 = 5, d = 2.
g)
Vậy số hạng đầu của cấp số cộng là u1 = 1, công sai là d = 3.
h)
Do
Với u2 = 3 và d = 2 thì u1 = u2 – d = 1.
Với u2 = 3 và d = –2 thì u1 = u2 – d = 5.
Vậy số hạng đầu của cấp số cộng là u1 = 1, công sai là d = 2 hoặc u1 = 5, d = –2.
i)
Từ (1), suy ra . Thay vào (2), ta có:
Vậy số hạng đầu của cấp số cộng là u1 = 1, công sai là d = 2 hoặc u1 = 7, d = –2.
k)
Từ (1), suy ra u1 = 1 – 2d. Thay vào (2), ta có:
Với d = 2 thì u1 = 1 – 2d = –3.
Với d = –2 thì u1 = 1 – 2d = 5.
Vậy số hạng đầu của cấp số cộng là u1 = –3, công sai là d = 2 hoặc u1 = 5, d = –2.
l)
Từ (1), suy ra u3 = 4. Thay vào (2), ta có:
Với u3 = 4 và d = –3 thì u1 = u3 – 2d = 10.
Với u3 = 4 và d = 3 thì u1 = u3 – 2d = –2.
Vậy số hạng đầu của cấp số cộng là u1 = 10, công sai là d = –3 hoặc u1 = –2, d = 3.
m)
Do
Với thì
.
Với thì
.
Vậy số hạng đầu của cấp số cộng là , công sai là
hoặc
,
.
n)
Từ (1), suy ra u1 + u4 = u2 + u3 = 10 và
Từ (2), ta có:
Với thì
Với thì
Với d = 2 thì u1 = 2
Với d = –2 thì u1 = 8
Vậy số hạng đầu của cấp số cộng là , công sai là
hoặc
,
hoặc u1 = 2, d = 2 hoặc u1 = 8, d = –2
o)
Khi đó ta có:
Mặt khác:
Vậy số hạng đầu của cấp số cộng là , công sai là
Câu 12. Xác định số hạng đầu, công sai và số hạng thứ n của các cấp số cộng sau, biết rằng:
a)
ĐS:
b)
ĐS: u1 = 86, d = –19
c)
ĐS: u1 = 0, d = 0
d)
ĐS: u1 = 0, d = 0
Lời giải.
a) Áp dụng công thức:
Trong đó u1 là số hạng đầu, d là công sai.
Ta có:
Vậy số hạng đầu là và công sai
b) Ta có:
Vậy số hạng đầu là u1 = 86 và công sai d = −19.
c)
Vậy số hạng đầu là u1 = 0 và công sai d = 0.
d)
Vậy số hạng đầu là u1 = 0 và công sai d = 0.
Câu 13. Cho cấp số cộng u1, u2, u3,… có công sai d.
a) Biết u2 + u22 = 40. Tính S23.
ĐS: S23 = 460
b) Biết u1 + u4 + u7 + u10 + u13 + u16 = 147. Tính A = u6 + u11 và B = u1 + u6 + u11 + u16.
ĐS: A = 49, B = 98
c) Biết u4 + u8 + u12 + u16 = 224. Tính S19.
ĐS: S19 = 1064
d) Biết u23 + u57 = 29. Tính C = u10 + u70 + u157 + 3u1.
ĐS: C = 87
Lời giải.
a) Ta có: u2 + u22 = 40
⇔ u1 + d + u1 + 21d = 40
⇔ 2u1 + 22d = 40.
Khi đó:
b) Ta có:
u1 + u4 + u7 + u10 + u13 + u16 = 147
⇔ u1 + u1 + 3d + u1 + 6d + u1 + 9d + u1 + 12d + u1 + 15d = 147
⇔ 6u1 + 45d = 147
⇔ 2u1 + 15d = 49
⇔ (u1 + 5d) + (u1 + 10d) = 49
⇔ u6 + u11 = 49.
Ta lại có:
2u1 + 15d = 49
⇔ 4u1 + 30d = 98
⇔ u1 + (u1 + 5d) + (u1 + 10d) + (u1 + 15d) = 98
⇔ u1 + u6 + u11 + u16 = 98.
c) Ta có:
u4 + u8 + u12 + u16 = 224
⇔ u1 + 3d + u1 + 7d + u1 + 11d + u1 + 15d = 224
⇔ 4u1 + 36d = 224
⇔ 2u1 + 18d = 112
⇔
⇔ S19 = 1064.
d) Ta có:
u23 + u57 = 29
⇔ 2u1 + 78d = 29
⇔ 6u1 + 234d = 87
⇔ (u1 + 9d) + (u1 + 69d) + (u1 + 156d) + 3u1 = 87
⇔ u10 + u70 + u157 + 3u1 = 87.
Câu 14. Tìm ba số hạng liên tiếp của một cấp số cộng, biết rằng:
a) Tổng của chúng bằng 15 và tích của chúng bằng 105.
ĐS: 3, 5, 7
b) Tổng của chúng bằng 15 và tổng bình phương của chúng bằng 83.
ĐS: 3, 5, 7
c) Tổng của chúng bằng 21 và tổng bình phương của chúng bằng 155.
ĐS: 5, 7, 9
Lời giải.
a) Gọi ba số hạng liên tiếp của cấp số cộng là x − d, x, x + d trong đó d là công sai.
Theo đề bài ta có:
Với d = 2 thì ba số hạng liên tiếp là 3, 5, 7.
Với d = −2 thì ba số hạng liên tiếp là 7, 5, 3.
Vậy ba số hạng liên tiếp của cấp số cộng là 3, 5, 7.
b) Gọi ba số hạng liên tiếp của cấp số cộng là x − d, x, x + d trong đó d là công sai.
Theo đề bài ta có:
Với d = 2 thì ba số hạng liên tiếp là 3, 5, 7.
Với d = −2 thì ba số hạng liên tiếp là 7, 5, 3.
Vậy ba số hạng liên tiếp của cấp số cộng là 3, 5, 7.
c) Gọi ba số hạng liên tiếp của cấp số cộng là x − d, x, x + d trong đó d là công sai.
Theo đề bài ta có:
Với d = 2 thì ba số hạng liên tiếp là 5, 7, 9.
Với d = −2 thì ba số hạng liên tiếp là 9, 7, 5.
Vậy ba số hạng liên tiếp của cấp số cộng là 5, 7, 9.
Câu 15. Tìm bốn số hạng liên tiếp của một cấp số cộng, biết rằng:
a) Tổng của chúng bằng 10 và tổng bình phương bằng 70.
ĐS: −2, 1, 4, 7
b) Tổng của chúng bằng 22 và tổng bình phương bằng 66.
ĐS: Không tồn tại
c) Tổng của chúng bằng 36 và tổng bình phương bằng 504.
ĐS: 0, 6, 12, 18
d) Chúng có tổng bằng 20 và tích của chúng bằng 384.
ĐS:
e) Tổng của chúng bằng 20, tổng nghịch đảo của chúng bằng và các số này là những số nguyên.
ĐS: 2, 4, 6, 8
f) Nó là số đo của một tứ giác lồi và góc lớn nhất gấp 5 lần góc nhỏ nhất.
ĐS: 30°, 70°, 110°, 150°
Lời giải.
a) Gọi bốn số hạng liên tiếp của cấp số cộng là x − 3d, x − d, x + d, x + 3d trong đó 2d là công sai.
Theo đề bài ta có:
Vậy bốn số hạng liên tiếp của cấp số cộng là −2, 1, 4, 7.
b) Gọi bốn số hạng liên tiếp của cấp số cộng là x − 3d, x − d, x + d, x + 3d trong đó 2d là công sai.
Theo đề bài ta có:
Vậy không tồn tại bốn số hạng liên tiếp của cấp số cộng thỏa mãn yêu cầu đề bài.
c) Gọi bốn số hạng liên tiếp của cấp số cộng là x − 3d, x − d, x + d, x + 3d trong đó 2d là công sai.
Theo đề bài ta có:
Vậy bốn số hạng liên tiếp của cấp số cộng là 0, 6, 12, 18.
d) Gọi bốn số hạng liên tiếp của cấp số cộng là x − 3d, x − d, x + d, x + 3d trong đó 2d là công sai.
Theo đề bài ta có:
Vậy bốn số hạng liên tiếp của cấp số cộng là 2, 4, 6, 8 hoặc ,
,
,
.
e) Gọi bốn số hạng liên tiếp của cấp số cộng là x − 3d, x − d, x + d, x + 3d trong đó 2d là công sai trong đó 2d ∈ ℤ.
Theo đề bài ta có:
Vậy bốn số hạng nguyên liên tiếp của cấp số cộng là 2, 4, 6, 8.
f) Gọi bốn số hạng liên tiếp của cấp số cộng xếp theo thứ tự tăng dần là x − 3d, x − d, x + d, x + 3d trong đó 2d > 0 là công sai.
Theo đề bài ta có:
Vậy bốn góc của tứ giác lồi lần lượt là 30°, 70°, 110°, 150°.
Câu 16. Tìm năm số hạng liên tiếp của một cấp số cộng, biết tổng của chúng bằng 40 và tổng bình phương của chúng bằng 480.
ĐS: 0, 4, 8, 12, 16
Lời giải.
Gọi năm số hạng liên tiếp của cấp số cộng là x − 2d, x − d, x, x + d, x + 2d trong đó d là công sai. Theo đề bài ta có:
Vậy năm số hạng liên tiếp của cấp số cộng là 0, 4, 8, 12, 16.
Câu 17. Một cấp số cộng có 7 số hạng với công sai d dương và số hạng thứ tư bằng 11. Hãy tìm các số hạng còn lại của cấp số cộng đó, biết hiệu của số hạng thứ ba và số hạng thứ năm bằng 6.
ĐS: 2, 5, 8, 11, 14, 17, 20
Lời giải.
Gọi số hạng đầu của cấp số cộng là u1, công sai d.
Vì số hạng thứ tư của cấp số cộng bằng 11 nên ta có: u4 = 11.
Do d dương nên u5 > u3.
Vì hiệu của số hạng thứ ba và số hạng thứ năm bằng 6 nên ta có u5 − u3 = 6. Ta có:
Vậy các số hạng còn lại của cấp số cộng là: u1 = 2, u2 = 5, u4 = 11, u6 = 17, u7 = 20.
Câu 18. Một cấp số cộng có 7 số hạng mà tổng của số hạng thứ ba và số hạng thứ năm bằng 28, tổng số hạng thứ năm và số hạng cuối bằng 140. Tìm cấp số cộng đó.
ĐS: −70, −42, −14, 14, 42, 70, 98
Lời giải.
Gọi số hạng đầu của cấp số cộng là u1, công sai d. Theo đề bài ta có:
Vậy cấp số cộng đó là: −70, −42, −14, 14, 42, 70, 98.
Câu 19. Viết sáu số xen giữa hai số 3 và 24 để được cấp số cộng có tám số hạng. Tìm cấp số cộng đó.
ĐS: 3, 6, 9, 12, 15, 18, 21, 24
Lời giải.
Gọi số hạng đầu của cấp số cộng là u1, công sai d. Theo đề bài ta có:
Vậy cấp số cộng đó là: 3, 6, 9, 12, 15, 18, 21, 24.
Câu 1. Giữa các số 7 và 35, hãy đặt thêm sáu số nữa để được một cấp số cộng.
ĐS: 7, 11, 15, 19, 23, 27, 31, 35
Lời giải.
Gọi số hạng đầu của cấp số cộng là u1, công sai d. Theo đề bài ta có:
Vậy cấp số cộng đó là: 7, 11, 15, 19, 23, 27, 31, 35.
Câu 20. Giữa các số 4 và 67, hãy đặt thêm 20 số nữa để được một cấp số cộng.
ĐS: u1 = 4, d = 3
Lời giải.
Gọi số hạng đầu của cấp số cộng là u1, công sai d. Theo đề bài ta có:
Vậy cấp số cộng đó là: 4, 7, 10, 13, 16, 19, 22, 25, 28, 31, 34, 37, 40, 43, 46, 49, 52, 55, 58, 61, 64, 67.
Câu 21. Một người trồng 3003 cây theo một hình tam giác như sau: “Hàng thứ nhất có một cây, hàng thứ hai có 2 cây, hàng thứ ba có 3 cây,…”. Hỏi có bao nhiêu hàng cây được trồng như thế?
ĐS: 77 hàng
Lời giải.
Gọi un là số cây trồng ở hàng thứ n.
Theo đề bài ta có u1 = 1; u2 = 2; u3 = 3,…
Dễ thấy un là cấp số cộng với số hạng đầu là u1 = 1, công sai d = 1.
Giả sử với 3003 cây trồng được n0 hàng. Khi đó ta có:
Vậy có 77 hàng được trồng.
Câu 22. Một công viên hình tam giác được trồng cây xanh theo hàng có quy luật của một cấp số cộng như sau: hàng thứ nhất có 9 cây, hàng thứ 10 có 54 cây, hàng cuối cùng có 2014 cây. Hỏi công viên đó có tất cả bao nhiêu cây được trồng?
ĐS: 406623 cây
Lời giải.
Gọi un là số cây trồng ở hàng thứ n,
Theo đề bài ta có un là cấp số cộng với: u1 = 9, u10 = 54, un = 2014.
Ta có: u10 = 54
⇔ u1 + 9d = 54 ⇔ d = 5.
Mặt khác: un = 2014
⇔ u1 + (n − 1)d = 2014
⇔ 9 + (n − 1)⋅5 = 2014
⇔ n = 402.
Khi đó tổng số cây của tất cả các hàng là:
Vậy công viên đó có tất cả 406623 cây được trồng.
Câu 23. Bạn A muốn mua món quà tặng mẹ và chị nhân ngày Quốc tế phụ nữ 8/3. Do đó A quyết định tiết kiệm từ ngày 1/1 của năm đó với ngày đầu là 500 đồng/ngày, ngày sau cao hơn ngày trước 500 đồng. Hỏi đúng đến ngày 8/3 bạn A có đủ tiền để mua quà cho mẹ và chị không? Giả sử rằng món quà A dự định mua khoảng 800 ngàn đồng và từ ngày 1/1 đến ngày 8/3 có số ngày ít nhất là 67 ngày.
Lời giải.
Gọi u1, u2, …, un là số tiền tiết kiệm của ngày 1/1, 2/1, …, 8/3.
Theo đề bài ta có (un) lập thành cấp số cộng với công sai d = 500.
Từ ngày 1/1 đến ngày 8/3, bạn A tiết kiệm được ít nhất là:
Vậy bạn A đủ tiền để mua quà cho mẹ mùng 8/3.
Câu 24. Một tòa nhà hình tháp có 30 tầng và tổng cộng có 1890 phòng, càng lên cao thì số phòng càng giảm, biết rằng cứ 2 tầng liên tiếp thì hơn kém nhau 4 phòng. Quy ước rằng tầng trệt là tầng 1, tiếp theo lên là tầng số 2, 3,… Hỏi tầng số 10 có bao nhiêu phòng?
ĐS: 85 phòng
Lời giải.
Gọi un là số phòng của tầng thứ n. Theo đề bài ta có:
u1 − u2 = u2 − u3 = u3 − u4 = … = u29 − u30 = 4
Nên (un) là cấp số cộng với công sai d = −4. Ta có:
Số hạng tổng quát của cấp số cộng là:
un = u1 + (n − 1)d = 121 − 4(n − 1) = −4n + 125.
Khi đó tầng 10 có số phòng là u10 = −4⋅10 + 125 = 85.
Câu 25. Khi ký hợp đồng dài hạn (10 năm) với các công nhân được tuyển dụng. Công ty liên doanh X đề xuất hai phương án trả lương để người lao động chọn, cụ thể là:
Phương án 1: Người lao động sẽ nhận 36 triệu đồng cho năm làm việc đầu tiên và kể từ năm thứ hai, mức lương sẽ được tăng thêm 3 triệu đồng mỗi năm.
Phương án 2: Người lao động sẽ được nhận 7 triệu đồng cho quý đầu tiên và kể từ quý làm việc thứ hai mức lương sẽ tăng thêm 500000 đồng mỗi quý.
Biết rằng mỗi năm có 4 quý. Nếu em là người lao động, em sẽ chọn phương án nào ?
ĐS: Phương án 2
Lời giải.
Theo đề bài, số tiền công nhân nhận được ở mỗi kỳ theo từng phương án lập thành một cấp số cộng, cụ thể:
Phương án 1:
Giá trị ban đầu u1 = 36 (triệu), công sai d = 3 (triệu).
Do hợp đồng kéo dài 10 năm nên n = 10.
Suy ra: u10 = u1 + (n − 1)⋅d = 36 + (10 − 1)⋅3 = 63 (triệu).
Vậy tổng số tiền lương nhận được của một công nhân khi hoàn thành hợp đồng (10 năm) là:
(triệu)
Phương án 2:
Giá trị ban đầu u1 = 7 (triệu), công sai d = 0,5 (triệu).
Do hợp đồng kéo dài 10 năm, mà mỗi năm có 4 quý nên n = 40.
Suy ra: u40 = u1 + (n − 1)⋅d = 7 + (40 − 1)⋅0,5 = 26,5 (triệu).
Vậy tổng số tiền lương nhận được của một công nhân khi hoàn thành hợp đồng (10 năm) là:
(triệu)
Vậy nếu là người lao động, em sẽ chọn phương án 2.
Câu 26. Tìm x để ba số a, b, c theo thứ tự đó lập thành một cấp số cộng với:
a) a = 10 − 3x, b = 2x2 + 3, c = 7 − 4x.
ĐS: x = hoặc x = 1
b) x = a2 − bc, y = b2 − ca, z = c2 − ab.
ĐS: x = 2y − z
Lời giải.
a) Để ba số a, b, c theo thứ tự lập thành một cấp số cộng thì
a + c = 2b
⇔ 10 − 3x + 7 − 4x = 2(2x2 + 3)
⇔ 4x2 + 7x − 11 = 0
⇔ x = ∨ x = 1
Vậy: x = và x = 1 thỏa yêu cầu bài toán.
b) Tương tự, để ba số a, b, c theo thứ tự lập thành một cấp số cộng thì:
a + c = 2b ⇔ a = 2b − c.
Do đó:
x = a2 − bc = (2b − c)2 − bc = 4b2 − 5bc + c2
y = b2 − ca = b2 − c(2b − c) = b2 − 2bc + c2
z = c2 − ab = c2 − b(2b − c) = −2b2 + bc + c2
Nhận xét: 2y − z = 4b2 − 5bc + c2 = x.
Vậy: x = 2y − z với y = b2 − ca, z = c2 − ab, a + c = 2b.
Câu 27. Tìm các nghiệm của phương trình: x3 − 15x2 + 71x − 105 = 0, biết rằng các nghiệm này phân biệt và chúng lập thành một cấp số cộng.
ĐS: 3, 5, 7
Lời giải.
Gọi x1, x2, x3 theo thứ tự là 3 nghiệm của phương trình đã cho.
Do x1, x2, x3 theo thứ tự lập thành một cấp số cộng.
Nên: x1 + x3 = 2x2 và d > 0 với d là công sai của cấp số cộng đã cho.
Mà theo định lý Vi-ét thì:
x1 + x2 + x3 = 15
⇔ 3x2 = 15 ⇔ x2 = 5.
Mặt khác: x1⋅x2⋅x3 = 105
⇔ x1⋅x3 = 21
⇔ (x2 − d)(x2 + d) = 21
⇔ 25 − d2 = 21
⇔ d = 2.
Vậy: x1 = 3, x2 = 5, x3 = 7.
Câu 28. Giải các phương trình sau:
a) 1 + 6 + 11 + 16 + 21 + … + x = 970.
ĐS: x = 96
b) 2 + 7 + 12 + 17 + 22 + ··· + x = 245.
ĐS: x = 47
c) (x + 1) + (x + 4) + (x + 7) + ··· + (x + 28) = 155.
ĐS: x = 1
d) (2x + 1) + (2x + 6) + (2x + 11) + ··· + (2x + 96) = 1010.
ĐS: x = 1
Lời giải.
a) Ta có: 1, 6, 11, …, x là một cấp số cộng với u1 = 1, un = x và d = 5.
Suy ra: un = u1 + (n − 1)⋅5 = 5n − 5
⇔ x = 5n − 4.
Mà: 1 + 6 + 11 + 16 + 21 + ··· + x = 970
⇔ (1).
Thay x = 5n − 4 vào (1), ta được:
Với n = 20 ⇒ x = 96.
Vậy x = 96 là nghiệm của phương trình đã cho.
b) Ta có: 2, 7, 12, …, x là một cấp số cộng với u1 = 2, un = x và d = 5.
Suy ra: un = u1 + (n − 1)⋅5 = 5n − 3
⇔ x = 5n − 3.
Mà: 2 + 7 + 12 + 17 + 22 + ··· + x = 245
⇔ (2).
Thay x = 5n − 3 vào (2), ta được:
Với n = 10 ⇒ x = 47.
Vậy x = 47 là nghiệm của phương trình đã cho.
c) Ta có: (x + 1), (x + 4), (x + 7), …, (x + 28) là một cấp số cộng với u1 = x + 1, un = x + 28 và d = 3.
Suy ra: un = u1 + (n − 1)⋅3
⇔ x + 28 = x + 1 + (n − 1)⋅3
⇔ n = 10.
Mà: (x + 1) + (x + 4) + (x + 7) + … + (x + 28) = 155
⇔ (3).
Thay n = 10 vào (3), ta được x = 1.
Vậy x = 1 là nghiệm của phương trình đã cho.
d) Ta có (2x + 1), (2x + 6), (2x + 11), …, (2x + 96) là một cấp số cộng với u1 = 2x + 1, un = 2x + 96 và d = 5.
Suy ra: un = u1 + (n − 1)⋅5
⇔ 2x + 96 = 2x + 1 + (n − 1)⋅5
⇔ n = 20.
Mà: (2x + 1) + (2x + 6) + (2x + 11) + … + (2x + 96) = 1010
⇔ (4).
Thay n = 20 vào (4), ta được x = 1.
Vậy x = 1 là nghiệm của phương trình đã cho.
Câu 29. Cho a, b, c là ba số hạng liên tiếp của một cấp số cộng. Chứng minh rằng:
a) a2 + 2bc = c2 + 2ab.
b) a2 + 8bc = (2b + c)2.
c) 2(a + b + c)3 = 9[a2(b + c) + b2(a + c) + c2(a + b)].
d) Ba số: a2 − bc, b2 − ac, c2 − ab cũng là một cấp số cộng.
e) Ba số: b2 + bc + c2, a2 + ac + c2, a2 + ab + b2 cũng là một cấp số cộng.
f) Ba số: ;
;
, (a, b, c > 0) cũng là một cấp số cộng.
Lời giải.
a) Vì a, b, c là ba số liên tiếp của một cấp số cộng nên a + c = 2b ⇒ a = 2b − c.
Do đó: a2 + 2bc
= (2b − c)2 + 2bc
= 4b2 − 2bc + c2
= 2b(2b − c) + c2
= 2ba + c2
= c2 + 2ab.
Vậy: a2 + 2bc = c2 + 2ab (đpcm).
b) Vì a, b, c là ba số liên tiếp của một cấp số cộng nên a + c = 2b ⇒ a = 2b − c.
Do đó: a2 + 8bc
= (2b − c)2 + 8bc
= 4b2 + 4bc + c2
= (2b + c)2.
Vậy a2 + 8bc = (2b + c)2 (đpcm).
c) Vì a, b, c là ba số liên tiếp của một cấp số cộng nên a + c = 2b ⇒ a = 2b − c.
Do đó:
VT = 2(a + b + c)3 = 2(3b)3 = 54b3
VP = 9 [a2(b + c) + b2(a + c) + c2(a + b)]
= 9 [(2b − c)2(b + c) + b2(2b − c + c) + c2(2b − c + b)]
= 9 [ (4b2 − 4bc + c2)(b + c) + b2(2b) + c2(3b − c)]
= 9 [4b3 − 4b2c + bc2 + 4b2c − 4bc2 + c3 + 2b3 + 3bc2 − c3]
= 9⋅(6b3) = 54b3 = VT .
Vậy: 2(a + b + c)3 = 9 [a2(b + c) + b2(a + c) + c2(a + b)] (đpcm).
d) Vì ba số a, b, c theo thứ tự lập thành một cấp số cộng thì a + c = 2b ⇒ a = 2b − c.
Do đó:
a2 − bc = (2b − c)2 − bc = 4b2 − 5bc + c2
b2 − ca = b2 − c(2b − c) = b2 − 2bc + c2
c2 − ab = c2 − b(2b − c) = −2b2 + bc + c2
Nhận xét: (a2 − bc) + (c2 − ab)
= (4b2 − 5bc + c2) + (−2b2 + bc + c2)
= 2b2 − 4bc +2c2
= 2(b2 − 2bc + c2)
= 2(b2 – ca)
Vậy ba số: a2 − bc, b2 − ac, c2 − ab là một cấp số cộng.
e) Vì ba số a, b, c theo thứ tự lập thành một cấp số cộng thì a + c = 2b ⇒ a = 2b − c.
Xét: 2(a2 + ac + c2) − (a2 + ab + b2)
= a2 + a(2c − b) + 2c2 − b2
= (2b − c)2 + (2b − c)(2c − b) + 2c2 − b2
= b2 + bc + c2
⇒ (b2 + bc + c2) + (a2 + ab + b2) = 2(a2 + ac + c2).
Vậy ba số: b2 + bc + c2, a2 + ac + c2, a2 + ab + b2 cũng là một cấp số cộng.
f) Vì ba số a, b, c theo thứ tự lập thành một cấp số cộng thì:
Ta có:
Vậy ba số: ;
;
, (a, b, c > 0) cũng là một cấp số cộng.
Câu 30. Cho ba số a2, b2, c2 theo thứ tự đó lập thành một cấp số cộng có công sai khác không.
Chứng minh rằng: cũng lập thành cấp số cộng.
Lời giải.
Vì ba số a2, b2, c2 theo thứ tự lập thành một cấp số cộng nên a2 + c2 = 2b2. Ta có:
Vậy ba số: cũng lập thành cấp số cộng.
Câu 31. Cho tam giác ABC có theo thứ tự đó lập thành cấp số cộng. Chứng minh cos A, cos B, cos C theo thứ tự cũng lập thành cấp số cộng.
Lời giải.
Ta có:
Vậy: cos A, cos B, cos C theo thứ tự cũng lập thành cấp số cộng.
Câu 32. Cho tam giác ABC có theo thứ tự lập thành cấp số cộng. Chứng minh ba cạnh: a, b, c theo thứ tự cũng lập thành cấp số cộng.
Lời giải.
Ta có:
Vậy ba cạnh: a, b, c theo thứ tự cũng lập thành cấp số cộng.
Câu 33. Tìm tham số m để phương trình f(x) = 0 có 4 nghiệm phân biệt lập thành một cấp số cộng trong các trường hợp sau:
a) f(x) = x4 − 2mx2 + 2m − 1.
ĐS: m = 5 hoặc m =
b) f(x) = x4 + 2(m + 1)x2 + 4.
ĐS: m =
c) f(x) = x4 + (3m + 5)x2 + (m + 1)2.
ĐS: Không có m thỏa mãn
d) f(x) = x4 − 10mx2 + 9m.
ĐS: m = 1
Lời giải.
a) Đặt t = x2 (t ≥ 0). Phương trình đã cho trở thành:
t2 − 2mt + 2m − 1 = 0 (1).
Ta phải tìm m sao cho (1) có hai nghiệm t1, t2 phân biệt dương phân biệt, tức là 0 < t1 < t2.
Đặt:
⇒ x1 < x2 < x3 < x4.
Để bốn nghiệm lập thành cấp số cộng thì:
Vậy ta có:
Vậy với thì phương trình đã cho có bốn nghiệm phân biệt lập thành một cấp số cộng.
b) Đặt t = x2 (t ≥ 0). Phương trình đã cho trở thành:
t2 + 2(m + 1)t + 4 = 0 (1)
Ta phải tìm m sao cho (1) có hai nghiệm t1, t2 phân biệt dương phân biệt, tức là 0 < t1 < t2.
Đặt:
⇒ x1 < x2 < x3 < x4.
Để bốn nghiệm lập thành cấp số cộng thì:
Vậy ta có:
Vậy với thì phương trình đã cho có bốn nghiệm phân biệt lập thành một cấp số cộng.
c) Đặt t = x2 (t ≥ 0). Phương trình đã cho trở thành:
t2 + (3m + 5)t + (m + 1)2 = 0 (1)
Ta phải tìm m sao cho (1) có hai nghiệm t1, t2 phân biệt dương phân biệt, tức là 0 < t1 < t2.
Đặt:
⇒ x1 < x2 < x3 < x4.
Để bốn nghiệm lập thành cấp số cộng thì:
Vậy ta có:
Vậy không có giá trị m để phương trình đã cho có bốn nghiệm phân biệt lập thành một cấp số cộng.
d) Đặt t = x2 (t ≥ 0). Phương trình đã cho trở thành:
t2 − 10mt + 9m = 0 (1)
Ta phải tìm m sao cho (1) có hai nghiệm t1, t2 phân biệt dương phân biệt, tức là 0 < t1 < t2.
Đặt
⇒ x1 < x2 < x3 < x4.
Để bốn nghiệm lập thành cấp số cộng thì:
Vậy ta có:
Vậy để phương trình đã cho có bốn nghiệm phân biệt lập thành một cấp số cộng thì m = 1.
Câu 34. Tìm tham số m để phương trình: x3 − (3m + 1)x2 + 2mx = 0 có 3 nghiệm phân biệt lập thành cấp số cộng?
ĐS: m =
Lời giải.
Ta có:
Để phương trình đã cho có ba nghiệm phân biệt thì phương trình (1) phải có hai nghiệm phân biệt khác 0, tức là:
Giả sử x1, x2 là hai nghiệm của phương trình (1) và x3 = 0, ta có:
Do vai trò của x1, x2 như nhau, ta chỉ cần xét hai trường hợp sau:
TH1: x1, x2 cùng dương hoặc cùng âm
Khi đó: x1 + x3 = 2x2 ⇒ x1 = 2x2.
Kết hợp với (I), ta có:
⇒ vô nghiệm, do đó không có m thỏa.
TH2: x1 và x2 trái dấu, x3 nằm giữa
Khi đó: x1 + x2 = 2x3 ⇒ x1 = −x2.
Kết hợp với (I) ta có:
Với m = phương trình đã cho có ba nghiệm lập thành một cấp số cộng.
Bạn đang xem bài viết Lý thuyết và các dạng bài tập phổ biến xem thêm các bài viết khác về chủ đề Toán lớp 11. Chúc bạn 1 ngày vui vẻ!