Toán lớp 10: Lý thuyết và phân dạng bài tập mới nhất 2023

Bạn đang xem bài viết Lý thuyết và phân dạng bài tập. Hi vọng sẽ là đáp án bạn ưng ý. Cùng theo dõi nhé!

Hệ thức lượng trong tam giác bao gồm định lý cosin, định lý sin, công thức tính đường trung tuyến, công thức tính diện tích, công thức hê rông và các hệ quả đi kèm. Việc nắm vững các công thức hệ thức lượng giúp tìm chính xác độ dài, diện tích hoặc yếu tố nào đó của tam giác nhanh chóng hơn.

Tóm tắt

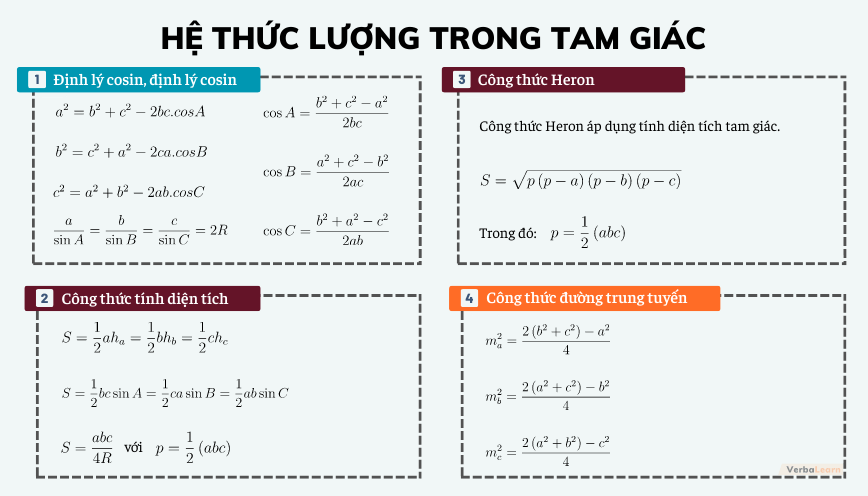
Hệ thức lượng trong tam giác

Cho tam giác ABC, BC = a, CA = b, Ab = c, S là diện tích tam giác. Giả sử h_a, h_b, h_c lần lượt là độ dài các đường cao đi qua ba đỉnh A, B, C; m_a, m_b, m_c lần lượt là các đường trung tuyến đi qua ba đỉnh A, B, C. R và r lần lượt là bán kính đường tròn ngoại tiếp và nội tiếp của tam giác ABC. Ta có kết quả sau đây:

Định lí cosin

a² = b² + c² – 2bc.cos A

b² = c² + a² – 2ca.cos B

c² = a² + b² – 2ab.cos C

⟹ Hệ quả của định lí cosin

$\begin{gathered} \cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}} \hfill \\ \hfill \\ \cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}} \hfill \\ \hfill \\ \cos C = \frac{{{b^2} + {a^2} - {c^2}}}{{2ab}} \hfill \\ \end{gathered}$

Định lí sin

$\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R$

Công thức diện tích

– $S = \frac{1}{2}a{h_a} = \frac{1}{2}b{h_b} = \frac{1}{2}c{h_c}$

– $S = \frac{1}{2}bc\sin A = \frac{1}{2}ca\sin B = \frac{1}{2}ab\sin C$

– $S = \frac{{abc}}{{4R}}$

– $S = pr$ với $p = \frac{1}{2}\left( {abc} \right)$

Công thức Hê – Rông

$S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)}$

Công thức trung tuyến

$\begin{gathered} m_a^2 = \frac{{2\left( {{b^2} + {c^2}} \right) - {a^2}}}{4} \hfill \\ \hfill \\ m_b^2 = \frac{{2\left( {{a^2} + {c^2}} \right) - {b^2}}}{4} \hfill \\ \hfill \\ m_c^2 = \frac{{2\left( {{a^2} + {b^2}} \right) - {c^2}}}{4} \hfill \\ \end{gathered}$

Phân dạng bài tập

Dạng 1. Giải tam giác

Phương pháp

Đề bài yêu cầu: Tìm một số yếu tố của tam giác khi cho biết các yếu tố khác.

Áp dụng các công thức sách giáo khoa như: định lí cosin, hệ quả của định lí cosin, định lí sin, các công thức liên quan đến diện tích để vận dụng vào làm bài.

Bài tập vận dụng

Câu 1. Cho tam giác có ABC có AB = 4, AC = 6, $\widehat A = 120^\circ$ . Tính độ dài cạnh BC.

Hướng dẫn giải

$\begin{gathered} B{C^2} = A{B^2} + A{C^2} - 2AB \cdot AC \cdot \cos A \hfill \\ \hfill \\ \begin{array}{*{20}{c}} {}&{} \end{array} = {6^2} + {4^2} - 2 \cdot 6 \cdot 4 \cdot \cos 120^\circ \hfill \\ \hfill \\ \begin{array}{*{20}{c}} {}&{} \end{array} = {6^2} + {4^2} - 2 \cdot 6 \cdot 4 \cdot \left( { - \frac{1}{2}} \right) = 76 \hfill \\ \hfill \\ \Rightarrow BC = \sqrt {76} = 2\sqrt {19} \hfill \\ \end{gathered}$

Câu 2. Cho tam giác ABC có a = 7; b = 8; c = 5. Tính $\widehat A,S,{h_a},R$

Hướng dẫn giải

$\begin{gathered} \cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}} = \frac{{{8^2} + {5^2} - {7^2}}}{{2 \cdot 8 \cdot 5}} = \frac{1}{2} \hfill \\ \begin{array}{*{20}{c}} {}&\begin{gathered} \hfill \\ \Rightarrow \widehat A = 60^\circ \hfill \\ \end{gathered} \end{array} \hfill \\ \hfill \\ S = \frac{1}{2}bc\sin A = \frac{1}{2}8 \cdot 5 \cdot \sin 60^\circ = 10\sqrt 3 \hfill \\ \hfill \\ S = \frac{1}{2}a{h_a} \Rightarrow {h_a} = \frac{{2S}}{a} = \frac{{2 \cdot 10\sqrt 3 }}{7} = \frac{{20\sqrt 3 }}{7} \hfill \\ \hfill \\ S = \frac{{abc}}{{4R}} \Rightarrow R = \frac{{abc}}{{4S}} = \frac{{7 \cdot 8 \cdot 5}}{{4 \cdot 10\sqrt 3 }} = \frac{{7\sqrt 3 }}{3} \hfill \\ \end{gathered}$

Câu 3. Cho tam giác ABC có độ dài ba cạnh là AB = 2, BC = 5, CA = 6. Tính độ dài đường trung tuyến MA, với M là trung điểm của BC.

Hướng dẫn giải

Áp dụng công thức tình độ dài trung tuyến ta có:

$\begin{gathered} MA = \sqrt {\frac{{A{B^2} + A{C^2}}}{2} - \frac{{B{C^2}}}{4}} \hfill \\ \hfill \\ \begin{array}{*{20}{c}} {}&{} \end{array} = \sqrt {\frac{{{2^2} + {6^2}}}{2} - \frac{{{5^2}}}{4}} = \frac{{\sqrt {55} }}{2} \hfill \\ \end{gathered}$

Câu 4. Tam giác ABC vuông tại A có AC = 6cm, BC = 10cm. Tính bán kính đường tròn nội tiếp tam giác ABC.

Hướng dẫn giải

Do tam giác ABC vuông tại A có AC = 6cm, BC = 10cm nên

$AB = \sqrt {B{C^2} - A{C^2}} = \sqrt {{{10}^2} - {6^2}} = 8$

Diện tích tam giác ABC là

${S_{\Delta ABC}} = \frac{1}{2}AB \cdot AC = 24$

Bán kính đường tròn nội tiếp tam giác ABC là

$r = \frac{{2{S_{\Delta ABC}}}}{{AB + BC + CA}} = \frac{{2 \cdot 24}}{{6 + 8 + 10}} = 2$

Câu 5. Cho tam giác ABC có b = 7, c = 5, cos A = $\frac{3}{5}$ . Tính độ dài đường cao h_a của tam giác ABC.

Hướng dẫn giải

Theo định lí hàm cos ta có:

$\begin{gathered} {a^2}{\text{ }} = {b^2} + {c^2} - 2bc\cos A \hfill \\ \begin{array}{*{20}{c}} {}&\begin{gathered} \hfill \\ = 49 + 25 - 2 \cdot 7 \cdot 5 \cdot \frac{3}{5} = 32 \hfill \\ \hfill \\ \end{gathered} \end{array} \hfill \\ \Rightarrow a = 4\sqrt 2 \hfill \\ \end{gathered}$

Ta lại có: $\cos A = \frac{3}{5} \Rightarrow \sin A = \frac{4}{5}$

Diện tích tam giác ABC là:

${S_{\Delta ABC}} = \frac{1}{2}bc\sin A = \frac{1}{2} \cdot 7 \cdot 5 \cdot \frac{4}{5} = 14$

Vì ${S_{\Delta ABC}} = \frac{1}{2}a{h_a}$ nên

${h_a} = \frac{{2{S_{\Delta ABC}}}}{a} = \frac{{28}}{{4\sqrt 2 }} = \frac{{7\sqrt 2 }}{2}$

Vậy ${h_a} = \frac{{7\sqrt 2 }}{2}$

Câu 6. Cho ΔABC có BC = a, $\widehat {BAC} = 120^\circ$ . Bán kính đường tròn ngoại tiếp ΔABC là

A. $R = \frac{{a\sqrt 3 }}{2}$

B. $R = \frac{a}{2}$

C. $R = \frac{{a\sqrt 3 }}{3}$

D. $R = a$

Hướng dẫn giải

Theo định lý sin trong tam giác ta có:

$2R = \frac{{BC}}{{\sin \widehat {BAC}}} \Rightarrow R = \frac{1}{2} \cdot \frac{a}{{\sin 120^\circ }} = \frac{{a\sqrt 3 }}{3}$

⟹ Chọn D.

Câu 7. Tam giác ABC có a = 8, c = 3, $\widehat B = 60^\circ$ . Độ dài cạnh b bằng bao nhiêu?

A. 49

B. 97

C. 7

D. 61

Hướng dẫn giải

b² = c² + a² – 2ca.cos B

= 8² + 3² – 2.8.3.cos 60° = 49

⇒ b = 7

⟹ Chọn C.

Câu 8. Cho ΔABC có a = 4, c = 5, $\widehat B = 150^\circ$ . Tính diện tích tam giác ABC.

A. S = 10

B. S =15

C. S = 5

D. S = 20

Hướng dẫn giải

Diện tích tam giác ABC là

$S = \frac{1}{2}ac\sin \widehat B = \frac{1}{2}4 \cdot 5 \cdot \sin 150^\circ = 5$

⟹ Chọn C.

Câu 9. Một tam giác có ba cạnh là 52, 56, 60. Bán kính đường tròn ngoại tiếp tam giác đó là

A. 65,4

B. 40

C. 32,5

D. 65,8

Hướng dẫn giải

Ta có: $p = \frac{{52 + 56 + 60}}{2} = 84$

Áp dụng hệ thức Hê – rông ta có:

$S = \sqrt {84\left( {84 - 52} \right)\left( {84 - 56} \right)\left( {84 - 60} \right)} = 1344$

Mặt khác:

$S = \frac{{abc}}{{4R}} \Rightarrow R = \frac{{abc}}{{4S}} = \frac{{52 \cdot 56 \cdot 60}}{{4 \cdot 1344}} = 32,5$

⟹ Chọn C.

Câu 10. Khoảng cách từ A đến B không thể đo trực tiếp được vì phải qua một đầm lầy. Người ta xác định được một điểm C mà từ đó có thể nhìn được A và B dưới một góc 60°. Biết CA = 200 (m), CB =180 (m). Khoảng cách AB bằng bao nhiêu?

A. 228 (m).

B. $20\sqrt {91}$ (m)

C. 112 (m).

D. 168 (m).

Hướng dẫn giải

AB² = CA² + CB² – 2CA.CB.cos 60° = 36400

⇒ AB = $20\sqrt {91}$ (m).

⟹ Chọn B.

Câu 11. Tam giác ABC có góc A nhọn, AB = 5, AC = 8, diện tích bằng 12. Tính độ dài cạnh BC.

A. 2

B. 4

C. 5

D. 3

Hướng dẫn giải

Ta có:

$\begin{gathered} S = \frac{1}{2}AB \cdot AC \cdot \sin A \hfill \\ \hfill \\ \Rightarrow \sin A = \frac{{2S}}{{AB \cdot AC}} = \frac{{2 \cdot 12}}{{5 \cdot 8}} = \frac{3}{5} \hfill \\ \hfill \\ \Rightarrow \widehat A = 36^\circ 52'12'' \hfill \\ \hfill \\ B{C^2} = A{B^2} + A{C^2} - 2AB \cdot AC \cdot \cos A \hfill \\ \hfill \\ \begin{array}{*{20}{c}} {}&{} \end{array} = {5^2} + {8^2} - 2 \cdot 5 \cdot 8 \cdot \cos 36^\circ 52'12'' \approx 25 \hfill \\ \hfill \\ \Rightarrow BC \approx 5 \hfill \\ \end{gathered}$

⟹ Chọn C.

Câu 12. Tam giác ABC có AB = 4, AC = 6 và trung tuyến BM = 3. Tính độ dài cạnh BC.

A. $\sqrt {17}$

B. $2\sqrt 5$

C. 4

D. 8

Hướng dẫn giải

$\begin{gathered} B{M^2} = \frac{{A{B^2} + A{C^2}}}{2} - \frac{{A{C^2}}}{4} \hfill \\ \hfill \\ \Rightarrow B{C^2} = 2\left( {B{M^2} + \frac{{A{C^2}}}{4}} \right) - A{B^2} \hfill \\ \hfill \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{} \end{array} = 2\left( {{3^2} + \frac{{{6^2}}}{4}} \right) - {4^2} = 20 \hfill \\ \hfill \\ \Rightarrow BC = 2\sqrt 5 \hfill \\ \end{gathered}$

⟹ Chọn B.

Câu 13. Tam giác ABC có AB = 4, AC =10 và đường trung tuyến AM = 6. Tính độ dài cạnh BC.

A. 6

B. 5

C. $\sqrt {22}$

D. $2\sqrt {22}$

Hướng dẫn giải

Ta có:

$\begin{gathered} A{M^2} = \frac{{A{C^2} + A{B^2}}}{2} - \frac{{B{C^2}}}{4} \hfill \\ \hfill \\ \Rightarrow B{C^2} = 4\left( {\frac{{A{C^2} + A{B^2}}}{2} - A{M^2}} \right) \hfill \\ \hfill \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{} \end{array} = 4\left( {\frac{{{{10}^2} + {4^2}}}{2} - {6^2}} \right) = 88 \hfill \\ \hfill \\ \Rightarrow BC = 2\sqrt {22} \hfill \\ \end{gathered}$

⟹ Chọn D.

Câu 14. Tam giác ABC có $\widehat A = 75^\circ ,\widehat B = 45^\circ ,AC = 2$ . Tính cạnh AB.

A. $\frac{{\sqrt 2 }}{2}$

B. $\sqrt 6$

C. $\frac{{\sqrt 6 }}{2}$

D. $\frac{{\sqrt 6 }}{3}$

Hướng dẫn giải

Ta có:

$\begin{gathered} \frac{b}{{\sin B}} = \frac{c}{{\sin C}} \hfill \\ \hfill \\ \Rightarrow AB = c = \frac{{b \cdot \sin C}}{{\sin B}} = \frac{{AC \cdot \sin C}}{{\sin B}} \hfill \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&\begin{gathered} \hfill \\ = \frac{{2\sin \left( {180^\circ - 75^\circ - 45^\circ } \right)}}{{\sin 45^\circ }} = \sqrt 6 \hfill \\ \end{gathered} \end{array} \hfill \\ \end{gathered}$

⟹ Chọn B.

Câu 15. Tam giác ABC có $\widehat B = 60^\circ ,\widehat C = 45^\circ ,AB = 3$ . Tính cạnh AC.

A. $\frac{{3\sqrt 6 }}{2}$

B. $\frac{{3\sqrt 2 }}{2}$

C. $\sqrt 6$

D. $\frac{{2\sqrt 6 }}{3}$

Hướng dẫn giải

Ta có:

$\begin{gathered} \frac{b}{{\sin B}} = \frac{c}{{\sin C}} \hfill \\ \hfill \\ \Rightarrow AC = b = \frac{{c \cdot \sin B}}{{\sin C}} = \frac{{AB \cdot \sin B}}{{\sin C}} \hfill \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&\begin{gathered} \hfill \\ = \frac{{3\sin 60^\circ }}{{\sin 45^\circ }} = \frac{{3\sqrt 6 }}{2} \hfill \\ \end{gathered} \end{array} \hfill \\ \end{gathered}$

⟹ Chọn A.

Câu 16. Tam giác ABC có các góc $\widehat A = 75^\circ ,\widehat B = 45^\circ$ . Tính tỉ số $\frac{{AB}}{{AC}}$ .

A. $\frac{{\sqrt 6 }}{3}$

B. $\sqrt 6$

C. $\frac{{\sqrt 6 }}{2}$

D. $\frac{{2\sqrt 6 }}{3}$

Hướng dẫn giải

Ta có:

$\begin{gathered} \frac{b}{{\sin B}} = \frac{c}{{\sin C}} \hfill \\ \hfill \\ \Rightarrow \frac{{AB}}{{AC}} = \frac{c}{b} = \frac{{\sin C}}{{\sin B}} \hfill \\ \hfill \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&\begin{gathered} = \frac{{\sin \left( {180^\circ - 75^\circ - 45^\circ } \right)}}{{\sin 45^\circ }} = \frac{{\sqrt 6 }}{2} \hfill \\ \hfill \\ \end{gathered} \end{array} \hfill \\ \end{gathered}$

⟹ Chọn C.

Câu 17. Tính bán kính đường tròn ngoại tiếp tam giác ABC biết AB = c và cos (A + B) = $\frac{1}{3}$ .

A. $\frac{{c\sqrt 2 }}{2}$

B. $\frac{{3c\sqrt 2 }}{8}$

C. $\frac{{9c\sqrt 2 }}{8}$

D. $\frac{{3c}}{2}$

Hướng dẫn giải

Ta có: $\cos C = - \cos \left( {A + B} \right) = - \frac{1}{3}$

Do đó: $\sin C = \sqrt {1 - {{\left( { - \frac{1}{3}} \right)}^2}} = \frac{{2\sqrt 2 }}{3}$

$\frac{{AB}}{{\sin C}} = 2R \Rightarrow R = \frac{{AB}}{{2\sin C}} = \frac{{3c\sqrt 2 }}{8}$

⟹ Chọn B.

Câu 18. Tam giác ABC có các góc $\widehat A = 105^\circ ,\widehat B = 45^\circ$ . Tính tỉ số $\frac{{AB}}{{AC}}$ .

A. $\frac{{\sqrt 2 }}{2}$

B. $\sqrt 2$

C. $\frac{{\sqrt 6 }}{2}$

D. $\frac{{\sqrt 6 }}{3}$

Hướng dẫn giải

Ta có:

$\begin{gathered} \frac{b}{{\sin B}} = \frac{c}{{\sin C}} \hfill \\ \hfill \\ \Rightarrow \frac{{AB}}{{AC}} = \frac{c}{b} = \frac{{\sin C}}{{\sin B}} \hfill \\ \hfill \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&\begin{gathered} = \frac{{\sin \left( {180^\circ - 105^\circ - 45^\circ } \right)}}{{\sin 45^\circ }} = \frac{{\sqrt 2 }}{2} \hfill \\ \hfill \\ \end{gathered} \end{array} \hfill \\ \end{gathered}$

⟹ Chọn A.

Câu 19. Tam giác ABC có AB = 4, AC = 5, BC = 6. Tính cos (B + C).

A. 0,125

B. –0,25

C. –0,125

D. 0,75

Hướng dẫn giải

Ta có: c = AB = 4, b = AC = 5, a = BC = 6.

$\cos A = \frac{{{b^2} + {a^2} - {a^2}}}{{2bc}} = \frac{1}{8}$

Để ý $\cos \left( {B + C} \right) = - \cos A = - \frac{1}{8} = - 0,125$

⟹ Chọn C.

Câu 20. Tam giác có ba cạnh lần lượt là 2, 3, 4. Góc bé nhất của tam giác có sin bằng bao nhiêu?

A. $\frac{{\sqrt {15} }}{8}$

B. $\frac{7}{8}$

C. $\frac{1}{2}$

D. $\frac{{\sqrt {14} }}{8}$

Hướng dẫn giải

Góc bé nhất ứng với cạnh có số đo bé nhất.

Giả sử: a = 2, b = 3, c = 4.

Ta có: $\cos A = \frac{{{b^2} + {a^2} - {a^2}}}{{2bc}} = \frac{7}{8}$

Do đó: $\sin A = \sqrt {1 - {{\left( {\frac{7}{8}} \right)}^2}} = \frac{{\sqrt {15} }}{8}$

⟹ Chọn A.

Câu 21. Tam giác có ba cạnh lần lượt là 3, 8, 9. Góc lớn nhất của tam giác có cosin bằng bao nhiêu?

A. $\frac{1}{6}$

B. $- \frac{1}{6}$

C. $\frac{{\sqrt {17} }}{4}$

D. $- \frac{4}{{25}}$

Hướng dẫn giải

Góc lớn nhất tương ứng với cạnh lớn nhất:

$\cos \alpha = \frac{{{3^2} + {8^2} - {9^2}}}{{2 \cdot 3 \cdot 8}} = - \frac{1}{6}$

⟹ Chọn B.

Câu 22. Hình vuông ABCD có cạnh bằng a. Gọi E là trung điểm cạnh BC, F là trung điểm cạnh AE. Tìm độ dài đoạn thẳng DF.

A. $\frac{{a\sqrt {13} }}{4}$

B. $\frac{{a\sqrt 5 }}{4}$

C. $\frac{{a\sqrt 3 }}{2}$

D. $\frac{{3a}}{4}$

Hướng dẫn giải

Ta có: $AE = DE = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 5 }}{2}$

Dùng công thức độ dài trung tuyến:

$\begin{gathered} D{F^2} = \frac{{D{A^2} + D{E^2}}}{2} - \frac{{A{E^2}}}{4} \hfill \\ \begin{array}{*{20}{c}} {}&{} \end{array} = \frac{\begin{gathered} \hfill \\ {a^2} + \frac{{5{a^2}}}{4} \hfill \\ \end{gathered} }{2} - \frac{{5{a^2}}}{{16}} = \frac{{13{a^2}}}{{16}} \hfill \\ \hfill \\ \Rightarrow DF = \frac{{a\sqrt {13} }}{4} \hfill \\ \end{gathered}$

⟹ Chọn A.

Câu 23. Tam giác ABC có BC =12, CA = 9, AB = 6. Trên cạnh BC lấy điểm M sao cho BM = 4. Tính độ dài đoạn thẳng AM

A. $2\sqrt 5$

B. $3\sqrt 2$

C. $\sqrt {20}$

D. $\sqrt {19}$

Hướng dẫn giải

$\begin{gathered} \cos B = \frac{{A{B^2} + B{C^2} - A{C^2}}}{{2AB \cdot BC}} \hfill \\ \begin{array}{*{20}{c}} {}&{\begin{array}{*{20}{c}} {}&\begin{gathered} \hfill \\ = \frac{{{6^2} + {{12}^2} - {9^2}}}{{2 \cdot 6 \cdot 12}} = \frac{{11}}{{16}} \hfill \\ \end{gathered} \end{array}} \end{array} \hfill \\ \hfill \\ AM = \sqrt {A{B^2} + B{M^2} - 2AB \cdot BM \cdot \cos B} \hfill \\ \begin{array}{*{20}{c}} {}&\begin{gathered} \hfill \\ \hfill \\ \hfill \\ \hfill \\ \end{gathered} \end{array} = \sqrt {{6^2} + {4^2} - 2 \cdot 6 \cdot 4 \cdot \frac{{11}}{{16}}} = \sqrt {19} \hfill \\ \end{gathered}$

⟹ Chọn D.

Câu 24. Tam giác ABC vuông tại A có AB = AC = a. Điểm M nằm trên cạnh BC sao cho $BM = \frac{{BC}}{3}$ . Độ dài AM bằng bao nhiêu?

A. $\frac{{a\sqrt {17} }}{3}$

B. $\frac{{a\sqrt 5 }}{3}$

C. $\frac{{2a\sqrt 2 }}{3}$

D. $\frac{{a\sqrt 5 }}{4}$

Hướng dẫn giải

$\begin{gathered} BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \hfill \\ \hfill \\ BC = AB\sqrt 2 = a\sqrt 2 \Rightarrow BM = \frac{{a\sqrt 2 }}{3} \hfill \\ \hfill \\ AM = \sqrt {A{B^2} + B{M^2} - 2AB \cdot BM \cdot \cos 45^\circ } \hfill \\ \hfill \\ \begin{array}{*{20}{c}} {}&{} \end{array} = \sqrt {{a^2} + {{\left( {\frac{{a\sqrt 2 }}{3}} \right)}^2} - 2 \cdot a \cdot \frac{{a\sqrt 2 }}{3} \cdot \frac{{\sqrt 2 }}{2}} = \frac{{a\sqrt 5 }}{3} \hfill \\ \end{gathered}$

⟹ Chọn B.

Câu 25. Tam giác ABC cos (A + B) = $- \frac{1}{8}$ , AC = 4, BC = 5. Tính cạnh AB.

A. 3

B. 9

C. 11

D. 6

Hướng dẫn giải

Vì trong tam giác ABC ta có A + B bù với góc C nên

$\begin{gathered} \cos \left( {A + B} \right) = - \frac{1}{8} \Rightarrow \cos C = \frac{1}{8} \hfill \\ \hfill \\ AB = \sqrt {A{C^2} + B{C^2} - 2AB \cdot BC \cdot \cos C} \hfill \\ \hfill \\ \begin{array}{*{20}{c}} {}&{} \end{array} = \sqrt {{4^2} + {5^2} - 2 \cdot 4 \cdot 5 \cdot \frac{1}{8}} = 6 \hfill \\ \end{gathered}$

⟹ Chọn D.

Câu 26. Tam giác ABC có AB = 7, AC = 5 và cos (B + C) = $- \frac{1}{5}$ . Tính BC.

A. $2\sqrt {15}$

B. $4\sqrt {22}$

C. $4\sqrt {15}$

D. $\sqrt {22}$

Hướng dẫn giải

Vì trong tam giác ABC ta có B + C bù với góc A nên

$\begin{gathered} \cos \left( {B + C} \right) = - \frac{1}{5} \Rightarrow \cos A = \frac{1}{5} \hfill \\ \hfill \\ BC = \sqrt {A{B^2} + A{C^2} - 2AB \cdot AC \cdot \cos A} \hfill \\ \hfill \\ \begin{array}{*{20}{c}} {}&{} \end{array} = \sqrt {{7^2} + {5^2} - 2 \cdot 7 \cdot 5 \cdot \frac{1}{5}} = 2\sqrt {15} \hfill \\ \end{gathered}$

⟹ Chọn A.

Câu 27. Tam giác ABC có BC = $\sqrt 5$ , AC = 3 và cot C = 2. Tính cạnh AB.

A. 6

B. $\sqrt 2$

C. 9

D. $2\sqrt {10}$

Hướng dẫn giải

Từ giả thiết cot C = 2, ta suy ra C là góc nhọn

$\begin{gathered} \cot C = 2 \Rightarrow \tan C = \frac{1}{2} \hfill \\ \hfill \\ \Rightarrow {\cos ^2}C = \frac{1}{{1 + {{\tan }^2}C}} = \frac{1}{\begin{gathered} 1 + {\left( { - \frac{1}{2}} \right)^2} \hfill \\ \hfill \\ \end{gathered} } = \frac{4}{5} \hfill \\ \Rightarrow \cos C = \frac{2}{{\sqrt 5 }} \hfill \\ \hfill \\ AB = \sqrt {A{C^2} + B{C^2} - 2AC \cdot BC \cdot \cos C} \hfill \\ \hfill \\ \begin{array}{*{20}{c}} {}&{} \end{array} = \sqrt {{3^2} + {{\sqrt 5 }^2} - 2 \cdot 3 \cdot \sqrt 5 \cdot \frac{2}{{\sqrt 5 }}} = \sqrt 2 \hfill \\ \end{gathered}$

⟹ Chọn B.

Câu 28. Tam giác ABC có AB = 3, AC = 4 và tan A = $- 2\sqrt 2$ . Tính cạnh BC.

A. $3\sqrt 2$

B. $4\sqrt 3$

C. $\sqrt {33}$

D. 7

Hướng dẫn giải

Từ giả thiết tan A = $- 2\sqrt 2$ , ta suy ra A là góc tù

$\begin{gathered} \tan A = - 2\sqrt 2 \hfill \\ \hfill \\ \Rightarrow {\cos ^2}A = \frac{1}{{1 + {{\tan }^2}A}} = \frac{1}{{1 + {{\left( { - 2\sqrt 2 } \right)}^2}}} = \frac{1}{9} \hfill \\ \hfill \\ \Rightarrow \cos A = - \frac{1}{3} \hfill \\ \hfill \\ BC = \sqrt {A{B^2} + A{C^2} - 2AB \cdot AC \cdot \cos A} \hfill \\ \hfill \\ \begin{array}{*{20}{c}} {}&{} \end{array} = \sqrt {{3^2} + {4^2} - 2 \cdot 3 \cdot 4 \cdot \left( { - \frac{1}{3}} \right)} = \sqrt {33} \hfill \\ \end{gathered}$

⟹ Chọn C.

Câu 29. Cho tam giác ABC có cạnh BC = a, cạnh CA = b. Tam giác ABC có diện tích lớn nhất khi góc C bằng:

A. 60°

B. 90°

C. 150°

D. 120°

Hướng dẫn giải

Diện tích của tam giác ABC là $S = \frac{1}{2}a \cdot b \cdot \sin C$

S lớn nhất khi sin C lớn nhất, hay $\sin C = 1 \Rightarrow \widehat C = 90^\circ$

⟹ Chọn B.

Câu 30. Cho tam giác MPQ vuông tại P. Trên cạnh MQ lấy hai điểm E F, sao cho các góc $\widehat {MPE}$ bằng nhau. Đặt MP = q, PQ = m, PE = x, PF = y. Trong các hệ thức sau, hệ thức nào đúng?

A. ME = EF = FQ

B. ME² = q² + x² – xq

C. MF² = q² + y² – yq

D. MQ² = q² + m² – 2qm

Hướng dẫn giải

Từ giả thiết, suy ra:

$\widehat {MPE} = \widehat {EPF} = \widehat {FPQ} = \frac{{\widehat {MPQ}}}{3} = 30^\circ$

Tam giác MPF có:

$\begin{gathered} \widehat {MPF} = \widehat {MPE} + \widehat {EPF} = 60^\circ \hfill \\ \hfill \\ M{F^2} = M{P^2} + P{F^2} - 2MP \cdot PF \cdot \cos \widehat {MPF} \hfill \\ \begin{array}{*{20}{c}} {}&{\begin{array}{*{20}{c}} {}&\begin{gathered} \hfill \\ = {q^2} + {y^2} - 2y \cdot q \cdot \frac{1}{2} = {q^2} + {y^2} - yq \hfill \\ \end{gathered} \end{array}} \end{array} \hfill \\ \end{gathered}$

⟹ Chọn C.

Câu 31. Tính góc C của tam giác ABC biết a ≠ b và a(a² – c²) = b(b² – c²).

A. C = 150°

B. C = 120°

C. C = 60°

D. C = 30°

Hướng dẫn giải

Ta có:

$\begin{gathered} a\left( {{a^2} - {c^2}} \right) = b\left( {{b^2} - {c^2}} \right) \hfill \\ \hfill \\ \Leftrightarrow {a^3} - {b^3} - {c^2}\left( {a - b} \right) = 0 \hfill \\ \hfill \\ \Leftrightarrow \left( {a - b} \right)\left( {{a^2} + ab + {b^2}} \right) - {c^2}\left( {a - b} \right) = 0 \hfill \\ \hfill \\ \Leftrightarrow {a^2} + ab + {b^2} - {c^2} = 0 \hfill \\ \hfill \\ \Rightarrow \cos C = \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}} = - \frac{1}{2} \hfill \\ \end{gathered}$

Do đó: C = 120°

⟹ Chọn B.

Câu 32. Tính bán kính đường tròn ngoại tiếp tam giác ABC biết AB = 12 và cot (A + B) = $\frac{1}{3}$ .

A. $2\sqrt {10}$

B. $\frac{{9\sqrt {10} }}{5}$

C. $5\sqrt {10}$

D. $3\sqrt 2$

Hướng dẫn giải

Ta có: cot (A + B) = $\frac{1}{3}$ nên cot C = $- \frac{1}{3}$ , suy ra: 3cos C = –sin C

Mà ${\sin ^2}C + {\cos ^2}C = 1$

$\begin{gathered} \Rightarrow \sin C = \frac{3}{{\sqrt {10} }} = \frac{{3\sqrt {10} }}{{10}} \hfill \\ \hfill \\ \frac{{AB}}{{\sin C}} = 2R \Rightarrow R = \frac{{AB}}{{2\sin C}} = 2\sqrt {10} \hfill \\ \end{gathered}$

⟹ Chọn A.

Câu 33. Tính bán kính đường tròn ngoại tiếp tam giác ABC biết AB = 10 và tan (A + B) = $\frac{1}{3}$ .

A. $\frac{{5\sqrt {10} }}{9}$

B. $\frac{{10}}{3}$

C. $\frac{{\sqrt {10} }}{5}$

D. $5\sqrt {10}$

Hướng dẫn giải

Ta có: tan (A + B) = $\frac{1}{3}$ nên tan C = $- \frac{1}{3}$ , suy ra: 3sin C = –cos C

Mà ${\sin ^2}C + {\cos ^2}C = 1$

$\begin{gathered} \Rightarrow \sin C = \frac{1}{{\sqrt {10} }} = \frac{{\sqrt {10} }}{{10}} \hfill \\ \hfill \\ \frac{{AB}}{{\sin C}} = 2R \Rightarrow R = \frac{{AB}}{{2\sin C}} = 5\sqrt {10} \hfill \\ \end{gathered}$

⟹ Chọn D.

Câu 34. Tam giác ABC có $AB = 4,AC = 6,\cos B = \frac{1}{8},\cos C = \frac{3}{4}$ .Tính cạnh BC. cos 4

A. 7

B. 5

C. 3

D. 2

Hướng dẫn giải

$\begin{gathered} \sin B = \sqrt {1 - {{\cos }^2}B} = \frac{{\sqrt {63} }}{8} \hfill \\ \hfill \\ \sin C = \sqrt {1 - {{\cos }^2}C} = \frac{{\sqrt 7 }}{4} \hfill \\ \hfill \\ \cos A = - \cos \left( {B + C} \right) \hfill \\ \hfill \\ \begin{array}{*{20}{c}} {}&{} \end{array}{\text{ }} = \sin B\sin C - \cos B\cos C = \frac{9}{{16}} \hfill \\ \end{gathered}$

Do đó: $BC = \sqrt {A{B^2} + A{C^2} - 2AB \cdot AC \cdot \cos A} = 5$

⟹ Chọn B.

Câu 35. Cho tam giác cân ABC có $\widehat A = 120^\circ$ và AB = AC = a. Lấy điểm M trên cạnh BC sao cho $BM = \frac{{2BC}}{5}$ . Tính độ dài AM

A. $\frac{{a\sqrt 3 }}{3}$

B. $\frac{{11a}}{5}$

C. $\frac{{a\sqrt 7 }}{5}$

D. $\frac{{a\sqrt 6 }}{4}$

Hướng dẫn giải

$\begin{gathered} BC = \sqrt {A{B^2} + A{C^2} - 2AB \cdot AC \cdot \cos 120^\circ } \hfill \\ \hfill \\ \begin{array}{*{20}{c}} {}&{} \end{array} = \sqrt {{a^2} + {a^2} - 2a \cdot a \cdot \left( { - \frac{1}{2}} \right)} = a\sqrt 3 \hfill \\ \hfill \\ \Rightarrow BM = \frac{{2a\sqrt 3 }}{5} \hfill \\ \hfill \\ AM = \sqrt {A{B^2} + B{M^2} - 2AB \cdot BM \cdot \cos 30^\circ } \hfill \\ \hfill \\ \begin{array}{*{20}{c}} {}&{} \end{array} = \sqrt {{a^2} + {{\left( {\frac{{2a\sqrt 3 }}{5}} \right)}^2} - 2a \cdot \frac{{2a\sqrt 3 }}{5} \cdot \frac{{\sqrt 3 }}{2}} \hfill \\ \hfill \\ \begin{array}{*{20}{c}} {}&{} \end{array} = \frac{{a\sqrt 7 }}{5} \hfill \\ \end{gathered}$

⟹ Chọn C.

Dạng 2. Hệ thức liên hệ giữa các yếu tố trong tam giác, nhận dạng tam giác

Phương pháp giải

Bài tập vận dụng

Câu 1. Cho tam giác ABC thỏa $\frac{{\sin A}}{{\sin B}} = 2\cos C$ . Tam giác ABC là tam giác gì?

Hướng dẫn giải

Ta có:

$\begin{gathered} \frac{{\sin A}}{{\sin B}} = 2\cos C \hfill \\ \hfill \\ \Leftrightarrow \frac{a}{b} = 2\cos C \hfill \\ \hfill \\ \Leftrightarrow a = 2b \cdot \cos C \hfill \\ \hfill \\ \Leftrightarrow a = 2b \cdot \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}} \hfill \\ \hfill \\ \Leftrightarrow {a^2} = {a^2} + {b^2} - {c^2} \hfill \\ \hfill \\ \Leftrightarrow b = c \hfill \\ \end{gathered}$

Tam giác ABC cân tại A.

Câu 2. Chứng minh trong tam giác ABC ta có: h_a = 2R.sin B.sin C

Hướng dẫn giải

Áp dụng định lí sin trong tam giác ta có:

$\frac{b}{{\sin B}} = 2R \Rightarrow 2R \cdot \sin B = b$

Do đó: h_a = 2R.sin B.sin C ⇔ h_a = b.sin C ( đúng)

Câu 3. Cho tam giác ABC. Chứng minh S =R.r (sin A + sin B + sin C)

Hướng dẫn giải

Ta có:

$\begin{gathered} {\text{VP}} = Rr\left( {\frac{a}{{2R}} + \frac{b}{{2R}} + \frac{c}{{2R}}} \right) \hfill \\ \hfill \\ \begin{array}{*{20}{c}} {}&{} \end{array} = r\left( {\frac{{a + b + c}}{2}} \right) = rp = S\left( {\rlap{--} Dpcm} \right) \hfill \\ \end{gathered}$

Câu 4. Cho tam giác ABC thỏa $\left\{ \begin{gathered} \frac{{{b^3} + {c^3} - {a^3}}}{{b + c - a}} = {a^2} \hfill \\ \hfill \\ a = 2b \cdot \cos C \hfill \\ \end{gathered} \right.$ . Chứng minh tam giác ABC là tam giác đều.

Hướng dẫn giải

Ta có:

$\begin{gathered} \left\{ \begin{gathered} \frac{{{b^3} + {c^3} - {a^3}}}{{b + c - a}} = {a^2} \hfill \\ \hfill \\ a = 2b \cdot \cos C \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} {b^3} + {c^3} - {a^3} = {a^2}b + {a^2}c - {a^3} \hfill \\ \hfill \\ a = 2b\frac{{{a^2} + {b^2} - {c^2}}}{{2ab}} \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} \left( {b + c} \right)\left( {{b^2} - bc + {c^2} - {a^2}} \right) = 0 \hfill \\ \hfill \\ a = 2b\frac{{{a^2} + {b^2} - {c^2}}}{{2ab}} \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} - bc + 2bc \cdot \cos A = 0 \hfill \\ {b^2} = {c^2} \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \Leftrightarrow \left\{ \begin{gathered} \cos A = \frac{1}{2} \hfill \\ \hfill \\ b = c \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} A = 60^\circ \hfill \\ b = c \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$

Vì tam giác ABC cân có 1 góc bằng 60° nên tam giác ABC là tam giác đều.

Câu 5. Chứng minh trong tam giác ABC ta có: sin B.cos C + sin C.cos B = sin A

Hướng dẫn giải

$\begin{gathered} {\text{VT}} = \frac{b}{{2R}} \cdot \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}} + \frac{c}{{2R}} \cdot \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}} \hfill \\ \hfill \\ \begin{array}{*{20}{c}} {}&{} \end{array} = \frac{{{a^2} + {b^2} - {c^2}}}{{4aR}} + \frac{{{a^2} + {c^2} - {b^2}}}{{4aR}} \hfill \\ \hfill \\ \begin{array}{*{20}{c}} {}&{} \end{array} = \frac{{2{a^2}}}{{4aR}} = \frac{a}{{2R}} = \sin A \hfill \\ \end{gathered}$

Câu 6. Cho tam giác ABC, chọn công thức đúng trong các đáp án sau:

A. $m_a^2 = \frac{{{b^2} + {c^2}}}{2} + \frac{{{a^2}}}{4}$

B. $m_a^2 = \frac{{{a^2} + {c^2}}}{2} - \frac{{{b^2}}}{4}$

C. $m_a^2 = \frac{{2{c^2} + 2{b^2} - {a^2}}}{4}$

D. $m_a^2 = \frac{{{a^2} + {b^2}}}{2} - \frac{{{c^2}}}{4}$

Hướng dẫn giải

Theo công thức đường trung tuyến ta có:

$m_a^2 = \frac{{{b^2} + {c^2}}}{2} - \frac{{{a^2}}}{4} = \frac{{2{c^2} + 2{b^2} - {a^2}}}{4}$

⟹ Chọn C.

Câu 7. Trong tam giác ABC, câu nào sau đây đúng?

A. a² = b² + c² + 2bc.cos A

B. a² = b² + c² – 2bc.cos A

C. a² = b² + c² + bc.cos A

D. a² = b² + c² – bc.cos A

Hướng dẫn giải

Áp dụng định lí hàm số cos tại đỉnh A ta có:

a² = b² + c² – 2bc.cos A

⟹ Chọn B.

Câu 8. Nếu tam giác ABC có a² < b² + c² thì:

A. $\widehat A$ là góc tù

B. $\widehat A$ là góc vuông

C. $\widehat A$ là góc nhọn

D. $\widehat A$ là góc nhỏ nhất

Hướng dẫn giải

Ta có:

$\begin{gathered} {a^2} = {b^2} + {c^2} - 2bc \cdot \cos A \hfill \\ \hfill \\ \Rightarrow \cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}} \hfill \\ \end{gathered}$

Do a² < b² + c² nên cos A > 0

⟹ Chọn C.

Câu 9. Tam giác ABC có ba cạnh thoả mãn điều kiện (a + b + c)(a + b – c) = 3ab. Khi đó số đo của $\widehat C$ là:

A. 120°

B. 30°

C. 45°

D. 60°

Hướng dẫn giải

Ta có: (a + b + c)(a + b – c) = 3ab

⇔ (a + b)² – c² = 3ab

⇔ a² + b² – c² = ab.

Theo hệ quả của định lí hàm cosin:

$\cos \widehat C = \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}} = \frac{{ab}}{{2ab}} = \frac{1}{2} \Rightarrow \widehat C = 60^\circ$

⟹ Chọn D.

Câu 10. Cho tam giác ABC. Khẳng định nào sau đây là đúng?

A. $m_a^2 + m_b^2 + m_c^2 = \frac{2}{3}\left( {{a^2} + {b^2} + {c^2}} \right)$

B. $m_a^2 + m_b^2 + m_c^2 = \frac{4}{3}\left( {{a^2} + {b^2} + {c^2}} \right)$

C. $m_a^2 + m_b^2 + m_c^2 = \frac{1}{3}\left( {{a^2} + {b^2} + {c^2}} \right)$

D. $m_a^2 + m_b^2 + m_c^2 = \frac{3}{4}\left( {{a^2} + {b^2} + {c^2}} \right)$

Hướng dẫn giải

Sử dụng công thức trung tuyến, ta có:

$\begin{gathered} m_a^2 + m_b^2 + m_c^2 \hfill \\ \hfill \\ = \frac{{2{b^2} + 2{c^2} - {a^2}}}{4} + \frac{{2{c^2} + 2{a^2} - {b^2}}}{4} + \frac{{2{a^2} + 2{b^2} - {c^2}}}{4} \hfill \\ \hfill \\ = \frac{3}{4}\left( {{a^2} + {b^2} + {c^2}} \right) \hfill \\ \end{gathered}$

⟹ Chọn D.

Câu 11. Cho tam giác ABC thỏa mãn c = a.cos B. Khẳng định nào sau đây là đúng?

A. Tam giác ABC là tam giác cân

B. Tam giác ABC là tam giác nhọn

C. Tam giác ABC là tam giác vuông

D. Tam giác ABC là tam giác tù

Hướng dẫn giải

Ta có:

$\begin{gathered} c = a\cos B \hfill \\ \hfill \\ \Leftrightarrow c = a \cdot \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}} \hfill \\ \hfill \\ \Leftrightarrow c = \frac{{{a^2} + {c^2} - {b^2}}}{{2c}} \hfill \\ \hfill \\ \Leftrightarrow {c^2} + {b^2} = {a^2} \hfill \\ \end{gathered}$

Theo định lí pi-ta-go tam giác ABC vuông tại A.

⟹ Chọn C.

Câu 12. Diện tích S của tam giác sẽ thỏa mãn hệ thức nào trong hai hệ thức sau đây?

I) S² = p(p – a)(p – b)(p – c)

II) 16S² = (a + b + c)(a + b – c)(a – b + c)( –a + b + c)

A. Chỉ I

B. Chỉ II

C. Cả I và II

D. Không có

Hướng dẫn giải

Ta có: I) đúng vì là công thức Hê-rông tính diện tích tam giác.

Khi đó:

$\begin{gathered} {S^2} = \frac{{a + b + c}}{2} \cdot \frac{{a + b - c}}{2} \cdot \frac{{a - b + c}}{2} \cdot \frac{{ - a + b + c}}{2} \hfill \\ \hfill \\ \Leftrightarrow 16{S^2} = \left( {a + b + c} \right)\left( {a + b - c} \right)\left( {a - b + c} \right)\left( { - a + b + c} \right) \hfill \\ \end{gathered}$

Do đó II) đúng

⟹ Chọn C.

Câu 13. Cho tam giác ABC, các đường cao h_a, h_b, h_c thỏa mãn hệ thức 3h_a = 2h_b + h_c. Tìm hệ thức giữa a, b, c.

A. $\frac{3}{a} = \frac{2}{b} - \frac{1}{c}$

B. 3a = 2b + c

C. 3a = 2b – c

D. $\frac{3}{a} = \frac{2}{b} + \frac{1}{c}$

Hướng dẫn giải

Kí hiệu S = S_∆_ABC

Ta có:

$\begin{gathered} 3{h_a} = 2{h_b} + {h_c} \hfill \\ \hfill \\ \Leftrightarrow \frac{{3 \cdot 2S}}{a} = \frac{{2 \cdot 2S}}{b} + \frac{{2S}}{c} \hfill \\ \hfill \\ \Leftrightarrow \frac{3}{a} = \frac{2}{b} + \frac{1}{c} \hfill \\ \end{gathered}$

⟹ Chọn D.

Câu 14. Trong tam giác ABC, hệ thức nào sau đây sai?

A. $a = \frac{{b \cdot \sin A}}{{\sin B}}$

B. $\sin C = \frac{{c \cdot \sin A}}{a}$

C. a = 2R.sin A

D. b = R.tan B

Hướng dẫn giải

Theo định lí hàm số sin ta có:

$\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R$

Suy ra:

$\begin{gathered} \frac{a}{{\sin A}} = \frac{b}{{\sin B}} \Rightarrow a = \frac{{b \cdot \sin A}}{{\sin B}} \hfill \\ \hfill \\ \frac{a}{{\sin A}} = \frac{c}{{\sin C}} \Rightarrow \sin C = \frac{{c \cdot \sin A}}{a} \hfill \\ \hfill \\ \frac{a}{{\sin A}} = 2R \Rightarrow a = 2R \cdot \sin A \hfill \\ \hfill \\ \frac{b}{{\sin B}} = 2R \Rightarrow \frac{b}{2} = R\sin B \Rightarrow \frac{b}{{2\cos B}} = R\tan B \hfill \\ \end{gathered}$

⟹ Chọn D.

Câu 15. Cho tam giác ABC thỏa mãn hệ thức b + c = 2a. Trong các mệnh đề sau, mệnh đề nào đúng?

A. cos B + cos C = 2cos A

B. sin B + sin C = 2sin A

C. sin B + sin C = sin A

D. sin B + cos C = 2sin A

Hướng dẫn giải

Ta có:

$\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R \Leftrightarrow \left\{ \begin{gathered} a = 2R\sin A \hfill \\ b = 2R\sin B \hfill \\ c = 2R\sin C \hfill \\ \end{gathered} \right.$

Mà: b + c = 2a

⇔ 2R.sin B + 2R.sin C = 4R.sin A

⇔ sin B + sin C = 2sin A

⟹ Chọn B.

Câu 16. Tam giác ABC có $\widehat A = 120^\circ$ thì câu nào sau đây đúng?

A. a² = b² + c² – 3bc

B. a² = b² + c² + bc

C. a² = b² + c² +3bc

D. a² = b² + c² – bc

Hướng dẫn giải

Áp dụng định lí hàm số cos tại đỉnh A ta có:

a² = b² + c² – 2bc.cos A

⇒ a² = b² + c² – 2bc.cos120°

⇒ a² = b² + c² + bc

⟹ Chọn B.

Câu 17. Trong tam giác ABC, điều kiện để hai trung tuyến vẽ từ A và B vuông góc với nhau là:

A. 2a² = 2b² + 5c²

B. 3a² = 3b² + 5c²

C. 2a² = 2b² + 3c²

D. a² = b² + 5c²

Hướng dẫn giải

Vì hai trung tuyến vẽ từ A và B vuông góc với nhau nên ∆ABG vuông tại G với G là trọng tâm tam giác ABC.

Khi đó:

$\begin{gathered} {c^2} = G{A^2} + G{B^2} \hfill \\ \hfill \\ \Leftrightarrow {c^2} = \frac{4}{9}\left( {\frac{{{b^2} + {c^2}}}{2} - \frac{{{a^2}}}{4} + \frac{{{a^2} + {c^2}}}{2} - \frac{{{b^2}}}{4}} \right) \hfill \\ \hfill \\ \Leftrightarrow {c^2} = \frac{4}{9}\left( {{c^2} + \frac{{{a^2}}}{4} + \frac{{{b^2}}}{4}} \right) \hfill \\ \hfill \\ \Leftrightarrow 5{c^2} = {a^2} + {b^2} \hfill \\ \end{gathered}$

⟹ Chọn D.

Câu 18. Trong tam giác ABC, nếu có a² = bc thì:

A. $\frac{1}{{h_a^2}} = \frac{1}{{{h_b}}} - \frac{1}{{{h_c}}}$

B. $h_a^2 = {h_b} \cdot {h_c}$

C. $\frac{1}{{h_a^2}} = \frac{1}{{{h_b}}} + \frac{1}{{{h_c}}}$

D. $\frac{1}{{h_a^2}} = \frac{2}{{{h_b}}} + \frac{2}{{{h_c}}}$

Hướng dẫn giải

Ta có:

$\begin{gathered} {a^2} = bc \hfill \\ \hfill \\ \Leftrightarrow {\left( {\frac{{2S}}{{{h_a}}}} \right)^2} = \left( {\frac{{2S}}{{{h_b}}}} \right) \cdot \left( {\frac{{2S}}{{{h_c}}}} \right) \hfill \\ \hfill \\ \Leftrightarrow \frac{1}{{h_a^2}} = \frac{1}{{{h_b}}} \cdot \frac{1}{{{h_c}}} \hfill \\ \hfill \\ \Leftrightarrow h_a^2 = {h_b} \cdot {h_c} \hfill \\ \end{gathered}$

⟹ Chọn B.

Câu 19. Trong tam giác ABC, nếu có 2h_a = h_b + h_c thì:

A. $\frac{2}{{\sin A}} = \frac{1}{{\sin B}} + \frac{1}{{\sin C}}$

B. 2sin A = sin B + sin C

C. sin A = 2sin B + 2sin C

D. $\frac{2}{{\sin A}} = \frac{1}{{\sin B}} - \frac{1}{{\sin C}}$

Hướng dẫn giải

Ta có:

$\begin{gathered} 2{h_a} = {h_b} + {h_c} \hfill \\ \hfill \\ \Leftrightarrow 2 \cdot \frac{{2S}}{a} = \frac{{2S}}{b} + \frac{{2S}}{c} \hfill \\ \hfill \\ \Leftrightarrow \frac{2}{a} = \frac{1}{b} + \frac{1}{c} \hfill \\ \hfill \\ \Leftrightarrow \frac{2}{{2R\sin A}} = \frac{1}{{2R\sin B}} + \frac{1}{{2R\sin C}} \hfill \\ \hfill \\ \Leftrightarrow \frac{2}{{\sin A}} = \frac{1}{{\sin B}} + \frac{1}{{\sin C}} \hfill \\ \end{gathered}$

⟹ Chọn A.

Câu 20. Trong tam giác ABC, câu nào sau đây đúng?

A. ${m_a} = \frac{{b + c}}{2}$

B. ${m_a} > \frac{{b + c}}{2}$

C. ${m_a} < \frac{{b + c}}{2}$

D. ${m_a} = b + c$

Hướng dẫn giải

Ta có:

$m_a^2 = \frac{{{b^2} + {c^2}}}{2} - \frac{{{a^2}}}{4} = \frac{{{{\left( {b + c} \right)}^2} + {{\left( {b - c} \right)}^2} - {a^2}}}{4}$

Vì $\left| {b - c} \right| < a \Rightarrow {\left( {b - c} \right)^2} < {a^2}$

$\Rightarrow m_a^2 < \frac{{{{\left( {b + c} \right)}^2}}}{4} \Leftrightarrow {m_a} < \frac{{b + c}}{2}$

⟹ Chọn C.

Câu 21. Tam giác ABC có các cạnh a, b, c thỏa mãn điều kiện (a + b + c)(a + b – c) = 3ab. Tính số đo của góc C.

A. 45°

B. 60°

C. 120°

D. 30°

Hướng dẫn giải

Ta có: (a + b + c)(a + b – c) = 3ab

⇔ (a + b)² – c² = 3ab

⇔ a² + b² – c² = ab

Mà: $\cos C = \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}} = \frac{1}{2} \Rightarrow \widehat C = 60^\circ$

⟹ Chọn B.

Câu 22. Cho tam giác ABC, xét các bất đẳng thức sau:

I) |a – b| < c

II) a < b + c

III) m_a + m_b + m_c < a + b + c

Hỏi khẳng định nào sau đây đúng?

A. Chỉ I, II

B. Chỉ II, III

C. Chỉ I, III

D. Cả I, II, III

Hướng dẫn giải

Ta có: I) và II) đúng vì đây là bất đẳng thức tam giác

Ta có:

$m_a^2 = \frac{{{b^2} + {c^2}}}{2} - \frac{{{a^2}}}{4} = \frac{{{{\left( {b + c} \right)}^2} + {{\left( {b - c} \right)}^2} - {a^2}}}{4}$

Vì $\left| {b - c} \right| < a \Rightarrow {\left( {b - c} \right)^2} < {a^2}$

$\Rightarrow m_a^2 < \frac{{{{\left( {b + c} \right)}^2}}}{4} \Leftrightarrow {m_a} < \frac{{b + c}}{2}$

Tương tự ta có:

${m_b} < \frac{{a + c}}{2};{\text{ }}{m_c} < \frac{{a + c}}{2}$

Do đó: m_a + m_b + m_c < a + b + c

Vậy III) Đúng.

⟹ Chọn D.

Câu 23. Tam giác ABC có các cạnh a, b, c thỏa mãn điều kiện ${b^2} + {c^2} - {a^2} = \sqrt 3 bc$ . Tính số đo của góc A.

A. 45°

B. 60°

C. 120°

D. 30°

Hướng dẫn giải

Ta có:

$\begin{gathered} {b^2} + {c^2} - {a^2} = \sqrt 3 bc \hfill \\ \hfill \\ \Leftrightarrow 2bc \cdot \cos A = \sqrt 3 bc \hfill \\ \hfill \\ \Leftrightarrow \cos A = \frac{{\sqrt 3 }}{2} \Rightarrow \widehat A = 30^\circ \hfill \\ \end{gathered}$

Mà $\cos C = \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}} = \frac{1}{2} \Rightarrow \widehat C = 60^\circ$

⟹ Chọn D.

Câu 24. Tam giác ABC, a.cos B = b.cos A. Tam giác ABC là tam giác gì?

A .Tam giác vuông

B. Tam giác đều

C. Tam giác vuông cân

D. Tam giác cân

Hướng dẫn giải

Ta có:

$\begin{gathered} a \cdot \cos B = b \cdot \cos A \hfill \\ \hfill \\ \Leftrightarrow a \cdot \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}} = b \cdot \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}} \hfill \\ \hfill \\ \Leftrightarrow {a^2} = {b^2} \Leftrightarrow a = b \hfill \\ \end{gathered}$

Vậy tam giác ABC cân.

⟹ Chọn D.

Câu 25. Cho tam giác ABC vuông tại A, AC = b, AB = c. Lấy điểm M trên cạnh BC sao cho góc $\widehat {BAM} = 30^\circ$ . Tính tỉ số $\frac{{MB}}{{MC}}$ .

A. $\frac{{b\sqrt 3 }}{{3c}}$

B. $\frac{{c\sqrt 3 }}{{3b}}$

C. $\frac{{c\sqrt 3 }}{b}$

D. $\frac{{b - c}}{{b + c}}$

Hướng dẫn giải

Ta có:

$\begin{gathered} \frac{{MB}}{{\sin 30^\circ }} = \frac{{AM}}{{\sin B}} \Rightarrow MB = \frac{{AM \cdot \sin 30^\circ }}{{\sin B}} = \frac{{AM}}{{2\sin B}} \hfill \\ \hfill \\ \frac{{MC}}{{\sin 60^\circ }} = \frac{{AM}}{{\sin C}} \Rightarrow MC = \frac{{AM \cdot \sin 60^\circ }}{{\sin C}} = \frac{{AM\sqrt 3 }}{{2\sin C}} \hfill \\ \end{gathered}$

Do đó: $\frac{{MB}}{{MC}} = \frac{{\sin C}}{{\sqrt 3 \sin B}} = \frac{c}{{\sqrt 3 b}} = \frac{{\sqrt 3 c}}{{3b}}$

⟹ Chọn B.

Câu 26. Mệnh đề nào sau đây sai?

A. Nếu a² > b² + c² thì A là góc tù

B. Nếu tam giác ABC có một góc tù thì a² > b² + c²

C. Nếu a² < b² + c² thì A là góc nhọn

D. Nếu a² = b² + c² thì A là góc vuông

Hướng dẫn giải

Ta có: $\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}$

Do đó:

– a² > b² + c² thì cos A < 0 do đó A là góc tù nên A đúng

– a² < b² + c² thì cos A > 0 do đó A là góc nhọn nên C đúng

– a² = b² + c² thì cos A = 0 do đó A là góc vuông nên D đúng

– Nếu tam giác ABC có góc B tù thì b² > a² + c²; nếu góc C tù thì c² > a² + b² do đó B sai

⟹ Chọn B.

Dạng 3: Ứng dụng hệ thức lượng trong thực tế

Phương pháp giải

Bài tập vận dụng

Câu 1. Hai chiếc tàu thuỷ cùng xuất phát từ vị trí A, đi thẳng theo hai hướng tạo với nhau một góc 60°. Tàu thứ nhất chạy với tốc độ 30 km/h, tàu thứ hai chạy với tốc độ 40 km/h. Hỏi sau 2 giờ hai tàu cách nhau bao nhiêu km ?

Hướng dẫn giải

Sau 2h quãng đường tàu thứ nhất chạy được là: S₁ = 30 × 2 = 60 km

Sau 2h quãng đường tàu thứ hai chạy được là: S₂ = 40 × 2 = 80 km

Vậy sau 2h hai tàu cách nhau là:

$S = \sqrt {S_1^2 + S_2^2 - 2{S_1} \cdot {S_2} \cdot \cos 60^\circ } = 20\sqrt {13}$

Câu 2. Từ một đỉnh tháp chiều cao CD = 80m, người ta nhìn hai điểm A và B trên mặt đất dưới các góc nhìn là 72°12′ và 34°26′ so với phương nằm ngang. Ba điểm A, B, D thẳng hàng. Tính khoảng cách AB (chính xác đến hàng đơn vị)?

Hướng dẫn giải

Trong tam giác vuông CDA:

$\begin{gathered} \tan 72^\circ 12' = \frac{{CD}}{{AD}} \hfill \\ \hfill \\ \Rightarrow AD = \frac{{CD}}{{\tan 72^\circ 12'}} = \frac{{80}}{{\tan 72^\circ 12'}} \simeq 25,7 \hfill \\ \end{gathered}$

Trong tam giác vuông CDB:

$\begin{gathered} \tan 34^\circ 26' = \frac{{CD}}{{BD}} \hfill \\ \hfill \\ \Rightarrow BD = \frac{{CD}}{{\tan 34^\circ 26'}} = \frac{{80}}{{\tan 34^\circ 26'}} \simeq 116,7 \hfill \\ \end{gathered}$

Suy ra khoảng cách AB = 116,7 – 25,7 = 91m

Câu 3. Cho tam giác ABC có a = 13, b = 8, c = 7. Tính góc A, suy ra S, h_a, R, r, m_a.

Hướng dẫn giải

$\begin{gathered} {a^2} = {b^2} + {c^2} - 2bc \cdot \cos A \hfill \\ \hfill \\ \Rightarrow \cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}} = - \frac{1}{2} \Rightarrow \widehat A = 120^\circ \hfill \\ \hfill \\ S = \frac{1}{2}bc \cdot \sin A = \frac{1}{2} \cdot 56 \cdot \frac{{\sqrt 3 }}{2} = 14\sqrt 3 \hfill \\ \hfill \\ S = \frac{1}{2}a \cdot {h_a} \Rightarrow {h_a} = \frac{{2S}}{a} = \frac{{28\sqrt 3 }}{{13}} \hfill \\ \hfill \\ S = \frac{{abc}}{{4R}} \Rightarrow R = \frac{{abc}}{{4S}} = \frac{{7 \cdot 8 \cdot 13}}{{4 \cdot 14\sqrt 3 }} = \frac{{13\sqrt 3 }}{3} \hfill \\ \hfill \\ S = pr \Rightarrow r = \frac{{2S}}{{a + b + c}} = \frac{{2 \cdot 14\sqrt 3 }}{{7 + 8 + 13}} = \sqrt 3 \hfill \\ \hfill \\ m_a^2 = \frac{{{b^2} + {c^2}}}{2} - \frac{{{a^2}}}{4} \Rightarrow {m_a} = \frac{{\sqrt {57} }}{2} \hfill \\ \end{gathered}$

Câu 4. Cho tam giác ABC có AB = 4, AC = 5 và cos A = $\frac{3}{5}$ . Tính cạnh BC, và độ dài đường cao kẻ từ A.

Hướng dẫn giải

Áp dụng định lí cosin ta có:

$\begin{gathered} B{C^2} = A{B^2} + A{C^2} - 2AB \cdot AC \cdot \cos A \hfill \\ \hfill \\ \begin{array}{*{20}{c}} {}&{} \end{array} = {4^2} + {5^2} - 2 \cdot 4 \cdot 5 \cdot \frac{3}{5} = 17 \hfill \\ \hfill \\ \Rightarrow BC = \sqrt {17} \hfill \\ \end{gathered}$

Vì sin²A + cos²A = 1 nên

$\sin A = \sqrt {1 - {{\cos }^2}A} = \sqrt {1 - \frac{9}{{25}}} = \frac{4}{5}$

Theo công thức tính diện tích ta có:

${S_{ABC}} = \frac{1}{2}AB \cdot AC \cdot \sin A = \frac{1}{2} \cdot 4 \cdot 5 \cdot \frac{4}{5} = 8{\text{ }}\left( 1 \right)$

Mặt khác: ${S_{ABC}} = \frac{1}{2}a \cdot {h_a} = \frac{1}{2} \cdot \sqrt {17} \cdot {h_a}{\text{ }}\left( 2 \right)$

Từ (1) và (2) suy ra: $\frac{1}{2} \cdot \sqrt {17} \cdot {h_a} = 8 \Rightarrow {h_a} = \frac{{16\sqrt {17} }}{{17}}$

Vậy độ dài đường cao kẻ từ A là ${h_a} = \frac{{16\sqrt {17} }}{{17}}$

Câu 5. Cho tam giác ABC có AB = 10, AC = 4 và $\widehat A = 60^\circ$ .

a) Tính chu vi của tam giác

b) Tính tan C

Hướng dẫn giải

a) Theo định lí cosin ta có:

BC² = 10² + 4² – 2.10.4.cos 60° = 76

⇒ BC ≈ 8,72

Suy ra chu vi tam giác là:

2p ≈ 10 + 4 + 8,72 = 22,72

Kẻ đường cao BH ta có:

AH = AB.cos 60° = 5

⇒ HC = 5 – 4 = 1

BH = AB.sin 60° = $5\sqrt 3$

Vậy $\tan C = - \tan \widehat {BCH} = - \frac{{HB}}{{HC}} = - 5\sqrt 3$

Câu 6. Giải tam giác ABC biết $\widehat A = 60^\circ ,\widehat B = 40^\circ ,c = 14$ .

Hướng dẫn giải

Ta có:

$\widehat C = 180^\circ - \widehat A - \widehat B = 180^\circ - 60^\circ - 40^\circ = 80^\circ$

Theo định lí sin ta có:

$\begin{gathered} a = \frac{{c \cdot \sin A}}{{\sin C}} = \frac{{14 \cdot \sin 60^\circ }}{{\sin 80^\circ }} \Rightarrow a \approx 12,3 \hfill \\ \hfill \\ b = \frac{{c \cdot \sin B}}{{\sin C}} = \frac{{14 \cdot \sin 40^\circ }}{{\sin 80^\circ }} \Rightarrow b \approx 9,1 \hfill \\ \end{gathered}$

Câu 7. Giải tam giác ABC, biết: $\widehat A = 30^\circ ,\widehat C = 75^\circ ,b = 4,5$

Hướng dẫn giải

Ta có:

$\widehat B = 180^\circ - \widehat A - \widehat C = 180^\circ - 30^\circ - 75^\circ = 75^\circ = \widehat C$

Suy ra tam giác ABC cận tại A ⇒ b = c = 4,5

Theo định lí sin ta có:

$a = \frac{{b \cdot \sin A}}{{\sin B}} = \frac{{4,5 \cdot \sin 30^\circ }}{{\sin 75^\circ }} \Rightarrow a \approx 2,33$

Câu 8. Cho tam giác ABC cân tại A biết $a = \sqrt 3 ,\widehat B = \widehat C = 30^\circ$ . Tính R, r, cạnh c, b, suy ra S.

Hướng dẫn giải

Áp dụng định lí sin:

$\begin{gathered} \frac{a}{{\sin A}} = 2R \Rightarrow R = \frac{a}{{2\sin A}} = \frac{{\sqrt 3 }}{\begin{gathered} 2 \cdot \frac{{\sqrt 3 }}{2} \hfill \\ \hfill \\ \end{gathered} } = 1 \hfill \\ \Rightarrow b = c = 2R\sin 30^\circ = 1 \hfill \\ \hfill \\ S = \frac{1}{2}bc \cdot \sin A = \frac{{\sqrt 3 }}{4} \hfill \\ \hfill \\ r = \frac{S}{p} = \frac{{\sqrt 3 }}{2}\left( {2 - \sqrt 3 } \right) \hfill \\ \end{gathered}$

Câu 9. Cho tam giác ABC nội tiếp đường tròn bán kính bằng 3, biết $\widehat A = 30^\circ ,\widehat B = 45^\circ$ . Tính độ dài trung tuyến kẻ từ A và bán kính đường tròn nội tiếp tam giác.

Hướng dẫn giải

Ta có:

$\widehat C = 180^\circ - \widehat A - \widehat B = 180^\circ - 30^\circ - 45^\circ = 105^\circ$

Theo định lí sin ta có:

$\begin{gathered} a = 2R \cdot \sin A = 2 \cdot 3 \cdot \sin 30^\circ = 3 \hfill \\ \hfill \\ b = 2R \cdot \sin B = 2 \cdot 3 \cdot \sin 45^\circ = 6 \cdot \frac{{\sqrt 2 }}{2} = 3\sqrt 2 \hfill \\ \hfill \\ c = 2R \cdot \sin C = 2 \cdot 3 \cdot \sin 105^\circ \approx 5,796 \hfill \\ \end{gathered}$

Theo công thức đường trung tuyến ta có:

$\begin{gathered} m_a^2 = \frac{{2\left( {{b^2} + {c^2}} \right) - {a^2}}}{4} \hfill \\ \begin{array}{*{20}{c}} {}&\begin{gathered} \hfill \\ \approx \frac{{2\left( {18 + 5,{{796}^2}} \right) - 9}}{4} = 23,547 \hfill \\ \end{gathered} \end{array} \hfill \\ \end{gathered}$

Theo công thức tính diện tích tam giác ta có:

$\begin{gathered} {S_{ABC}} = pr = \frac{1}{2}bc \cdot \sin A \hfill \\ \hfill \\ \Rightarrow r = \frac{{bc \cdot \sin A}}{{2p}} \approx \frac{{3\sqrt 2 \cdot 5,796 \cdot \sin 30^\circ }}{{3 + 3\sqrt 2 + 5,796}} \approx 0,943 \hfill \\ \end{gathered}$

Câu 10. Cho tam giác ABC thỏa mãn sin² A = sin B.sin C. Chứng minh rằng

a) a² = bc

b) $\cos A \geqslant \frac{1}{2}$

Hướng dẫn giải

a) Áp dụng định lí sin ta có:

$\sin A = \frac{a}{{2R}},{\text{ }}\sin B = \frac{b}{{2R}},{\text{ }}\sin C = \frac{c}{{2R}}$

Suy ra:

$\begin{gathered} {\sin ^2}A = \sin B \cdot \sin C \hfill \\ \hfill \\ \Leftrightarrow {\left( {\frac{a}{{2R}}} \right)^2} = \frac{b}{{2R}} \cdot \frac{c}{{2R}} \hfill \\ \hfill \\ \Leftrightarrow {a^2} = bc{\text{ }}\left( {\rlap{--} Dpcm} \right) \hfill \\ \end{gathered}$

b) Áp dụng định lí cosin và câu a) ta có:

$\begin{gathered} \cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}} = \frac{{{b^2} + {c^2} - bc}}{{2bc}} \hfill \\ \hfill \\ \begin{array}{*{20}{c}} {}&{} \end{array} \geqslant \frac{{2bc - bc}}{{2bc}} = \frac{1}{2}{\text{ }}\left( {\rlap{--} Dpcm} \right) \hfill \\ \end{gathered}$

Câu 11. Tam giác ABC có BC = a, CA = b, AB = c và trung tuyến AM = AB = c chứng minh rằng:

a) a² = 2(b² – c²)

b) sin²A = 2(sin²B – sin²C)

Hướng dẫn giải

a) Áp dụng công thức đường trung tuyến

Ta có:

$\begin{gathered} {b^2} + {c^2} = \frac{{{a^2}}}{2} + 2A{M^2} = \frac{{{a^2}}}{2} + 2{c^2} \hfill \\ \hfill \\ \Rightarrow {a^2} = 2\left( {{b^2} - {c^2}} \right){\text{ }}\left( * \right) \hfill \\ \end{gathered}$

b) Theo định lí sin ta có:

$\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R \Rightarrow \left\{ \begin{gathered} {a^2} = 4{R^2}{\sin ^2}A \hfill \\ {b^2} = 4{R^2}{\sin ^2}B \hfill \\ {c^2} = 4{R^2}{\sin ^2}C \hfill \\ \end{gathered} \right.$

Thay vào (*) ta có đpcm

Câu 12. Cho tam giác ABC. Chứng minh rằng điều kiện cần và đủ để hai trung tuyến kẻ từ B và C vuông góc với nhau là b² + c² = 5a².

Hướng dẫn giải

Gọi G là trọng tâm của tam giác ABC.

Khi đó hai trung tuyến kẻ từ B và C vuông góc với nhau khi và chỉ khi tam giác GBC vuông tại G

$\begin{gathered} \Leftrightarrow G{B^2} + G{C^2} = B{C^2} \hfill \\ \hfill \\ \Leftrightarrow {\left( {\frac{2}{3}{m_b}} \right)^2} + {\left( {\frac{2}{3}{m_c}} \right)^2} = {a^2}{\text{ }}\left( * \right) \hfill \\ \end{gathered}$

Mặt khác theo công thức đường trung tuyến ta có:

$m_b^2 = \frac{{2\left( {{a^2} + {c^2}} \right) - {b^2}}}{4},{\text{ }}m_c^2 = \frac{{2\left( {{a^2} + {b^2}} \right) - {c^2}}}{4}$

Suy ra:

$\begin{gathered} \left( * \right) \Leftrightarrow \frac{4}{9}\left( {m_b^2 + m_c^2} \right) = {a^2} \hfill \\ \hfill \\ \Leftrightarrow \frac{4}{9}\left[ {\frac{{2\left( {{a^2} + {c^2}} \right) - {b^2}}}{4} + \frac{{2\left( {{a^2} + {b^2}} \right) - {c^2}}}{4}} \right] = {a^2} \hfill \\ \hfill \\ \Leftrightarrow 4{a^2} + {b^2} + {c^2} = 9{a^2} \hfill \\ \hfill \\ \Leftrightarrow {b^2} + {c^2} = 5{a^2} \hfill \\ \end{gathered}$

Câu 13. Chứng minh rằng trong mọi tam giác ABC ta có:

a) a = b.cos C + c.cos B

b) sin A = sin B.cos C + sin C.cos B

Hướng dẫn giải

a) Áp dụng định lí cosin ta có:

$\begin{gathered} {\text{VP}} = b \cdot \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}} + c \cdot \frac{{{c^2} + {a^2} - {b^2}}}{{2ca}} \hfill \\ \begin{array}{*{20}{c}} {}&\begin{gathered} \hfill \\ = \frac{{{a^2} + {b^2} - {c^2} + {c^2} + {a^2} - {b^2}}}{{2a}} = a = {\text{VT}} \hfill \\ \end{gathered} \end{array} \hfill \\ \end{gathered}$

b) $\sin A = \sin B \cdot \cos C + \sin C \cdot \cos B$

$\begin{gathered} \Leftrightarrow \frac{a}{{2R}} = \frac{b}{{2R}} \cdot \cos C + \frac{c}{{2R}} \cdot \cos B \hfill \\ \hfill \\ \Leftrightarrow a = b \cdot \cos C + c \cdot \cos B \hfill \\ \end{gathered}$

Câu 14. Chứng minh rằng trong mọi tam giác ABC ta có: h_a = 2R.sin B.sin C

Hướng dẫn giải

$\begin{gathered} {h_a} = 2R \cdot \sin B \cdot \sin C \hfill \\ \hfill \\ \Leftrightarrow \frac{{2S}}{a} = 2R \cdot \frac{b}{{2R}} \cdot \sin C \hfill \\ \hfill \\ \Leftrightarrow S = \frac{1}{2}ab\sin C \hfill \\ \end{gathered}$

Câu 15. Tìm tính chất đặc biệt của tam giác ABC biết: 2a.cos A = b.cos C + c.cos B

Hướng dẫn giải

Yêu cầu bài toán tương đương với:

$\begin{gathered} 2\left( {2R\sin A} \right)\cos A = 2R\sin B\cos C + 2R\sin C\cos B \hfill \\ \hfill \\ \Leftrightarrow 2\sin A\cos A = \sin \left( {B + C} \right) = \sin A \hfill \\ \hfill \\ \Leftrightarrow \cos A = \frac{1}{2}\left( {{\text{do }}\sin A \ne 0} \right) \hfill \\ \hfill \\ \Leftrightarrow \widehat A = 60^\circ \hfill \\ \end{gathered}$

Câu 16. Nhận dạng tam giác ABC biết: $\left\{ \begin{gathered} a = 2b \cdot \cos C{\text{ }}\left( 1 \right) \hfill \\ \hfill \\ {a^2} = \frac{{{a^3} - {b^3} - {c^3}}}{{a - b - c}}{\text{ }}\left( 2 \right) \hfill \\ \end{gathered} \right.$

Hướng dẫn giải

Áp dụng định lí cosin ở (1) và thế vào (2)

$\begin{gathered} \left( 1 \right) \Leftrightarrow a = \frac{{{a^2} + {b^2} - {c^2}}}{a} \Leftrightarrow b = c \hfill \\ \hfill \\ \left( 2 \right) \Leftrightarrow {a^2} = {b^2} + {c^2} - bc \hfill \\ \hfill \\ \Leftrightarrow \cos A = \frac{1}{2} \Leftrightarrow \widehat A = 60^\circ \hfill \\ \end{gathered}$

Kết luận: Tam giác ABC đều.

Câu 17. Nhận dạng tam giác ABC biết: a.sin A + b.sin B + c.sin C = h_a + h_b + h_c.

Hướng dẫn giải

Áp dụng công thức diện tích ta có:

$S = \frac{1}{2}bc \cdot \sin A = \frac{1}{2}a \cdot {h_a}$

Suy ra:

$\begin{gathered} a \cdot \sin A + b \cdot \sin B + c \cdot \sin C = {h_a} + {h_b} + {h_c} \hfill \\ \hfill \\ \Leftrightarrow a \cdot \frac{{2S}}{{bc}} + b \cdot \frac{{2S}}{{ca}} + c \cdot \frac{{2S}}{{ab}} = \frac{{2S}}{a} + \frac{{2S}}{b} + \frac{{2S}}{c} \hfill \\ \hfill \\ \Leftrightarrow {a^2} + {b^2} + {c^2} = ab + bc + ca \hfill \\ \hfill \\ \Leftrightarrow {\left( {a - b} \right)^2} + {\left( {b - c} \right)^2} + {\left( {c - a} \right)^2} = 0 \hfill \\ \hfill \\ \Leftrightarrow a = b = c \hfill \\ \end{gathered}$